1.3. Краевые условия

К начальным условиям не предъ­является дополнительных требований аналогии, так как они им всегда удовлетворяют. К граничным условиям такие требования предъявляются. Рассмотрим области задания уравнений (1.18) и (1.10). Областью задания уравнения переноса энергии (1.18), как условились, является переходный слой насыщенного газа. Только в нем энтальпии газа однозначно соответствует его темпе­ратура. Этого нельзя сказать о взаимном соответствии влагосодержания газа и концентрации пара. Действительно, на границе с жидкостью влагосодержание газа формально равно бесконеч­ности, так как входящая в знаменатель концентрация газа вслед­ствие непроницаемости жидкости стремится к нулю. В то же время концентрация пара имеет конечное значение, определяе­мое параметрами состояния. В слое же ненасыщенного газа обес­печивается взаимное однозначное соответствие концентрации пара и влагосодержания газа при постоянной энтальпии газа. Поэтому целесообразно в качестве области задания уравнения переноса массы (1.10) рассмотреть пограничный слой ненасыщенного газа.

Приведем уравнение (1.18) к безразмерному виду следующей заменой переменных:

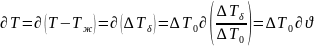
Здесь 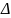Т₀ = Т_м – T_ж – локальный температурный напор, соот­ветствующий разности температур на границах переходного на­сыщенного слоя в пределах бесконечно малого объема; Т_ж – температура газа на границе с жидкостью; T_м – температура газа на границе слоев насыщенного и ненасыщенного газа; = Т – Т_ж – текущий локальный температурный напор в переход­ном слое при изменении Т от Т_ж до T_м; – толщина переход­ного слоя.

После преобразований уравнение (1-18) запишется в прежней форме

(1.19)

граничные условия к нему запишутся следующим образом:

(1.20)

где 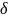_т = / ₀ – относительная толщина переходного слоя, равная нулю на границе с жидкостью и единице – на границе с нена­сыщенным газом.

Аналогичные выкладки можно сделать и для уравнения диф­фузии, в котором переменной будет относительный концентра­ционный напор, а областью задания – слой ненасыщенного газа с изменяющимся Влагосодержанием:

(1.21)

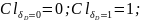(1.22)

1.4. Аналогия процессов тепло- и массообмена

Как отмечалось, формальная сущность аналогии тепло- и массообмена состоит в требовании тождественности их уравнений и условий однозначности.

Из уравнений (1.10) и (1.18)'или (1.19) и (1.21) следует, что температурное поле в слое насыщенного газа и поле концентраций в слое ненасыщенного газа не зависит от физических свойств среды, а полностью определяются формой рассматриваемого тела. Другими словами, тепло- и массообмен между жидкостью и газом при их непосредственном контакте автомоделен относительно чисел подобия, включающих только физические характеристики сред, в том числе относительно числа Льюиса Lе = a/D, числа Прандтля Рr = v/a и др. В данном случае форма примыкающих друг к другу слоев насыщенного и ненасыщенного газа является одинаковой и для теплообмена и для массообмена, уравнения переноса энергии и массы и краевые условия к ним для своих областей задания являются полностью тождественными друг другу относительно переменных ϑ и С. Этим самым утверждается аналогия процессов тепло- и массообмена при непосредственном контакте газа и жидкости.

Из тождественности уравнений следует, что будут тождествен­ными их решения, поля и градиенты переменных:

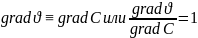(1.23)

Теперь запишем гипотезы Фурье и Фика в безразмерном виде:

N'u = grad ; (1.24)

N'u_D = grad C; (1.25)

С учетом уравнения (1.23) отношение чисел Нуссельта, тепло­вого и диффузионного, будет равно единице:

(1.26)

Это соотношение является одной из количественных зависи­мостей, устанавливаемых с помощью понятия аналогии процес­сов тепло- и массообмена. Как видно, оно заключается в равенст­ве безразмерных характеристик интенсивности тепло- и массооб­мена в соответствующих слоях насыщенного и ненасыщенного газа. Из тождественности локальных следует тождественность средних чисел Нуссельта, теплового и диффузионного, За весь процесс в целом:

Nu ≡ Nu_D . (1.27)