Получим

.

С учетом аналогии процессов тепло- и массообмена

;

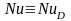где Nu– критерий Нуссельта;

Nu_D– критерий Нуссельта диффузионный;

выражение (5.26) существенно упрощается:

или

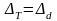. (2.28)

Таким образом, коэффициенты интенсивности теплообмена и массообмена равны между собой, если они представлены отноше­нием средних за весь процесс движущих сил к максимальным. При этом, процесс теплообмена рассматривается применительно к пограничному слою насыщенного, а массообмен – к слою не­насыщенного газа. Полученная из уравнений интенсивности теплообмена и массообмена зависимость (2.28) является уравнением относительной интенсивности тепло- и массообмена [1].

Значения величин, входящих в уравнение относительной ин­тенсивности тепло- и массообмена, могут отклоняться от законо­мерности, представленной формулой (2.28), из-за погрешности измерений при проведении экспериментальных исследований. Ввиду тождественности полей потенциалов переноса массы и энергии способ вычисления средней за весь процесс движущей силы теплообмена и массообмена не должен оказывать влияния на соблюдение равенства (2.28). Более того, всегда найдется такое направление в объеме реактивного пространства, относи­тельно которого распределение потенциалов переноса будет ли­нейным, так как уравнение (2.28) содержит только начальные и конечные параметры состояния сред и ничем не связано с фак­торами, определяющими это направление. Тогда, движущие силы можно вычислять как средние арифметические напоры:

температурный

; (2.29)

концентрационный

. (2.30)

Совместное решение уравнения (2.28) с (2.29) или (2.30) дает возможность получить в явном виде зависимость для любого из включенных в них параметров, например, для конечного влагосодержания газа, являющегося вторым (после T_м2) искомым па­раметром газа.

, кг/кг. (2.31)

В реальных условиях проведения процессов тепло- и массообмена в контактных аппаратах d₂≤d_м2, так как всегда имеются центры конденсации влаги и перенасыщения газа в аппаратах практически не наступает. Согласно этому неравенству и уравне­нию (2.29) Δ_d≤0,5. Для величины Δ_T такие ограничения отсут­ствуют.

Таким образом, аналитически получено уравнение относитель­ной интенсивности тепло- и массообмена в контактной системе охлаждения, связывающее между собой только начальные и конечные параметры сред в виде прос­той алгебраической зависимости (2.27). Поскольку не было сделано соответствующих допущений, это уравнение справедливо для любых сред, их парамет­ров и схем взаимного движения, т.к. оно является математиче­ским выражением некоторой общей закономерности процессов тепло- и массообмена. Физическая сущность этой закономерности заключается в равновесии, которое устанавливается между от­носительной движущей силой теплообмена в насыщенном газе и относительной движущей силой массообмена в ненасыщен­ном газе.

2.5. Гидродинамическая устойчивость газожидкостной системы

Рассмотрим равновесие газа и жидкости при образовании капель. В силу вязкостного трения газ захватывает частицы жидкости, деформируя ее поверхность с об­разованием волн. Если силы поверхностного натяжения меньше сил, определяемых скоростным напором газа, то с гребней волн отрываются капли, происходит их унос, т. е., нарушение гидроди­намической устойчивости газожидкостной системы. Отрыв капель происходит на границе между газом и жидкостью, т. е. в зоне дей­ствия сил вязкостного трения – ламинарной зоне, для которой коэффициент трения определяется законом Пуазейля: ζ = A₁/Rе. Запишем условие начала образования капли диаметром d, когда ее внутреннее давление от сил поверхностного натяжения уравно­вешивается скоростным напором:

, (2.32)

где ζ– коэффициент лобового сопротивления; A₁– постоянный коэффициент;

d– диаметр капли, м; σ_w– коэффициент поверхностного натяжения жидкости, н/м.

После сокращения получаем некоторую постоянную безразмер­ную величину, определяющую начало образования капель:

.

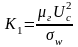Эта величина не полностью характеризует процесс, так как капля быстро покидает ламинарную зону и попадает в турбу­лентную. Однако, уноса не будет, если вес капли равен силе, обу­словленной скоростным напором:

;

;

,

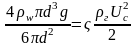где g – ускорение свободного падения.

Подставив 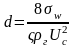из уравнения (2.32), получаем второй критерий устойчивости – критерий Кутателадзе [1], характеризую­щий условия после начала образования капель:

.

Разделение газожидкостной смеси в центробежном сепараторе начинается, когда скоростной напор, действующий на каплю уравновешивается центробежной силой:

; .

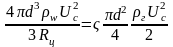Соотношение (5.32) справедливо и для условий распыления жидкости в смесителе, тогда подставив , и проведя соответствующие преобразования, получим третий критерий – критерий начала центробежной сепарации:

.

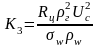Критерий K₂ определяет максимальную скорость газа, при которой отсутствует капельный унос жидкости по причине срыва пленки со стенок аппарата, критерий K₃ определяет максимальную скорость газа, при которой возможно центробежное разделение. Тогда, стабильная работа воздухоохладителя, с точки зрения отсутствия капельного уноса, обеспечивается при условиях Ku<Ku_кр и K₃<K_3кр.

Для условий в устье аппарата расчетные параметры должны быть отнесены к начальным – для жидкости и к конечным – для газа.

По критерию устойчивости газожидкостной системы Ku прове­ряют аппарат на предельный расход газа в таком же ши­роком диапазоне режимных параметров и теплофизических свойств сред, как и по другим зависимостям, приведенным в данной работе.