Міністерство освіти і науки, молоді та спорту України

ДВНЗ «Криворізький національний університет»

Кафедра теплоенергетики

МЕТОДИЧНИЙ ПОСІБНИК

з дисципліни

«СПЕЦІАЛЬНІ ПИТАННЯ ТепломасообмінУ»

Для студентів спеціальності 8.05060101 - Теплоенергетика

Кривий Ріг

2013

Укладач: Замицький О.В. д.т.н., проф.

1. Особенности процессов в контактных аппаратах и методов расчета

1.1. Основы расчета процессов в тепломассообменных аппаратах

Основой современных методов расчета тепло- и массообмена являются дифференциальные уравнения движения, неразрывности, теплопроводности и диффу­зии. В совокупности с условиями однозначности они составляют систему уравнений, решения которой дают иско­мые поля скоростей, температур и концентраций среды. Названные уравнения выведены для бесконечно малого объема среды и отражают элементарный акт переноса субстанции: массы, энергии и количества движения (импульса). Общее дифференциальное урав­нение переноса субстанции записывается в следующем виде

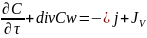(1.1)

где dC/dτ – локальное изменение (во времени) концентрации субстанции; div Cw – конвективная составляющая переноса субстанции; j – вектор диффузионного (молекулярного) переноса - плотность потока субстанции; J_V – мощность источников и стоков субстанции.

В задачах тепло- и массообмена уравнение (1.1) справедливf в том случае, если область задания функции не включает границу раздела фаз. Граница раздела фаз является источником или стоком среды при испарении и конденсации, но поскольку она ис­ключается из области задания функции, то при отсутствии других источников (химические реакции, радиоактивный распад вещества и др.) J_v = 0. В дальнейшем будем рассматривать именно такие процессы, в которых J_v = 0.

Следует отметить, что тепло- и массообмен во влажном газе при определенных условиях сопровождается туманообразованием – объемной конденсацией пара, связанной с появлением мельчайших капель жидкости, взвешенных в газопаровой смеси. Это происходит тогда, когда парциальное давление р_п пара в смеси становится больше давления насыщения p_s то есть когда пар становится пересыщенным. Процесс объемной конденса­ции пара происходит скачком, с очень большой скоростью, По­скольку в аппаратах технических систем всегда есть центры кон­денсации (мелкие твердые частицы, газовые ионы и др.), то критическая степень пересыщения близка к единице и конденса­ция может начаться практически по достижении состояния на­сыщения газа. Туман плохо осаждается на поверхностях и яв­ляется стоком пара и одновременно источником теплоты, которая выделяется при конденсации пара и расходуется на нагрев при­легающих слоев холодного газа. Более того, над поверхностью жидкости всегда есть слой насыщенного газа, в котором при пере­менной температуре слоя и наличии центров конденсации туманообразование является неизбежным, так как зависимость р_п = f(t), определяемая кинетикой переноса массы и энергии, и за­висимость p_s = f(t), определяемая физическими свойствами жид­кости, не совпадают. Совпадение давлений (р_п =p_s) имеет место только на верхней и нижней границах слоя, а между границами избыток пара переходит в туман.

Однако туманообразование пока рассматривать не будем из следующих соображений. Во многих случаях, когда влагосодержа­ние газа невелико, образованием тумана в пограничном слое можно пренебречь ввиду незначительного количества. При анали­зе расчетных зависимостей необходимо выделять и исследовать влияние основных факторов – теплопроводности и диффузии – на взаимосвязанные процессы тепло- и массообмена во влажном газе при его непосредственном контакте в первую очередь с основ­ной массой капель или пленок жидкости, а уже потом – с тума­ном. При получении эмпирических зависимостей влияние различ­ных неучтенных факторов, в том числе туманообразования, ниве­лируется значениями коэффициентов и показателей степеней при числах подобия, определяемыми опытным путем. В зависимостях, основанных на аналогии тепло- и массобмена и представляющих собой равенства каких-либо относительных эффектов, например движущих сил, неучтенные при их аналитическом выводе факторы могут взаимно компенсировать друг друга, полностью или частич­но исключая свое влияние на эти зависимости. Учет влияния на тепло- и массообмен различных факторов, в том числе тумано­образования, более всего необходим при аналитическом способе расчета параметров процесса, так как в этом случае исключение какого-либо фактора ухудшает точность расчета.

Одной из специфических особенностей протекания процессов тепло- и массообмена в контактных аппаратах является ограниче­ние относительной скорости газа и жидкости (по условия капель­ного уноса). Например, в аппаратах при непосредственном кон­такте воздуха и воды относительная скорость, как правило, не превышает 3 м/с. Реже она составляет 10–12 м/с. При этом поток газа в самом аппарате может достигать существенно более высоких скоростей. Другой особенностью является наличие фазо­вых переходов, обеспечивающих невысокий температурный и кон­центрационный напор.

Характерные для процессов тепло- и массообмена при непосредственном контакте сред низкие относительные скорости газа и жидкости, разности температур, концентраций и давлений позво­ляют существенно упростить дифференциальные уравнения пере­носа массы и энергии в пограничном слое газа с жидкостью, в том числе пренебречь эффектами термо- и бародиффузии работой внешних сил и диссипацией энергии, считать газ несжимаемой средой.

Уравнение неразрывности для несжимаемой среды имеет про­стой вид:

(1.2)

Используя уравнение (1.2) и соотношениие div Сw = wgrad C+Cdiv w = wgradC, получим общее уравнение переноса субстан­ции в упрощенном виде

(1.3)

где – полная, субстанцио­нальная производная.