Завдання

Таблиця 4. 3 

Маса, кг		Довжина нитки, м	Жорсткість пружини, Н/м	Початкові умови
				, м	, град	, м/с	, рад/с
1	0,1	0,5	10	0,2	15	0	0

Виконання

1. Складемо рівняння Лагранжа іі роду

Для розв’язання задачі застосуємо рівняння Лагранжа ІІ роду. Оскільки задана механічна система має дві степені вільності, то необхідно ввести дві узагальнені координати, за які виберемо: переміщення повзуна і кут відхилення від вертикалі нитки математичного маятника. Отже, будемо мати два диференціальних рівняння руху еліптичного маятника відповідно до вибраних узагальнених координат у вигляді

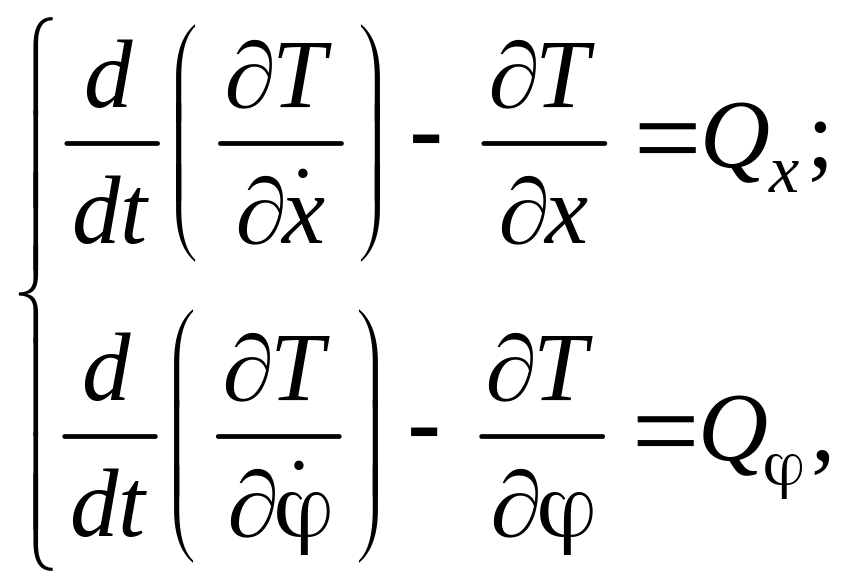(4.188)

де – кінетична енергія еліптичного маятника, який складається з повзуна масою та кульки математичного маятника масою , а і – узагальнені сили.

Оскільки всі сили, що діють на систему, потенціальні, то перепишемо систему рівнянь Лагранжа ІІ роду (4.188) у вигляді

(4.189)

де – лагранжіан, – потенціальна енергія.

Складемо вираз для кінетичної енергії еліптичного маятника як функції узагальнених швидкостей та узагальнених координат .

Кінетична енергія дорівнює сумі кінетичних енергій повзуна та кульки , тобто

, (4.190)

де – кінетична енергія повзуна , який рухається поступально,

. (4.191)

– кінетична енергія кульки , яка здійснює складний рух,

, (4.192)

де – абсолютна швидкість кульки (див. рис. 4.36);

,

де – відносна швидкість, що відповідає коловому руху кульки математичного маятника , – переносна швидкість математичного маятника разом з повзуном . У проекціях на осі, вказані на рис. 4.36, абсолютна швидкість дорівнює

(4.193)

Тоді

, (4.194)

Таким чином,

. (4.195)

Визначимо потенціальну енергію на узагальнених переміщеннях і повзуна та кульки, до яких прикладені сили.

, (4.196)

Тут – потенціальна енергія сили пружності, – потенціальна енергія сили ваги кульки, які відповідно дорівнюють

Рисунок  4.36

, (4.197)

де – висота підйому кульки з нижнього положення.

Отже, лагранжіан еліптичного маятника

. (4.198)

За допомогою комп’ютера

2. Знайдемо власні частоти коливань.

Далі складаємо програму в середовищі Maple, за допомогою якої змоделюємо рух механічної системи [ 8 ]. У табл. 4.4 текст програми розбито на блоки з метою детального пояснення змісту елементів математичного моделювання динаміки механізму.

Рекомендації щодо написання програми для визначення власних частот коливань еліптичного маятника (див. табл. 4.4).

Блок 1 є обов’язковим для будь-якої програми, а підпрограма, що використовується у блоці 2 вже змодельована на кафедрі теоретичної механіки і студент може її взяти у готовому вигляді з додатку № 2 до РГР.

Примітка: у готовій підпрограмі при бажанні можна змінювати тільки кольори графічних об’єктів в операторі .

Блок 3 є стандартними та обов’язковими для створення динаміки системи – підключення графічних пакетів.

У блоці:

• студент вводить геометричні розміри еліптичного маятника згідно виданому завданню (табл. 4.4);

• на дисплей комп’ютера виводиться зображення еліптичного маятника;

• вводять вирази для кінетичних енергій повзуна (4.194), кульки (4.195) та системи (4.190);

• вводять вирази для потенціальних енергій сили пружності, ваги кульки (4.192) та системи (4.196);

• вводять вираз для функції Лагранжа (4.198);

• визначають усі частинні похідні від функції Лаг- ранжа за змінними, які входять до рівнянь Лагранжа ІІ роду;

• формують систему рівнянь Лагранжа ІІ роду та зводять її до одного диференціального рівняння руху еліптичного маятника;

• складають характеристичне рівняння з метою визначення власних частот коливань еліптичного маятника;

• визначають корені характеристичного рівняння у символьному вигляді;

• визначають динамічні параметри еліптичного маятника;

• розраховують та виводять на друк власні частоти коливань еліптичного маятника.

Примітка: у готовій програмі при бажанні можна змінювати геометричні та динамічні параметри і досліджувати зміну при цьому власних частот коливань, а також вивести вирази для визначення цих частот у символьному вигляді (для цього у блоці 12 необхідно змінити знак « : » на « ; »).