4.3.7. Дослідження амплітудно-частотних характеристик системи

Дослідимо стаціонарний розв’язок (4.149). Розглянемо амплітуду В і зсув фази . На підставі (4.147) і (4.148)

;

(4.151)

.

Перейдемо у виразах (4.151) до безрозмірних параметрів, узявши

. (4.152)

Зауважимо, що на підставі (4.144)

, (4.153)

де – статичне зміщення системи під впливом статичної сили . Отже,

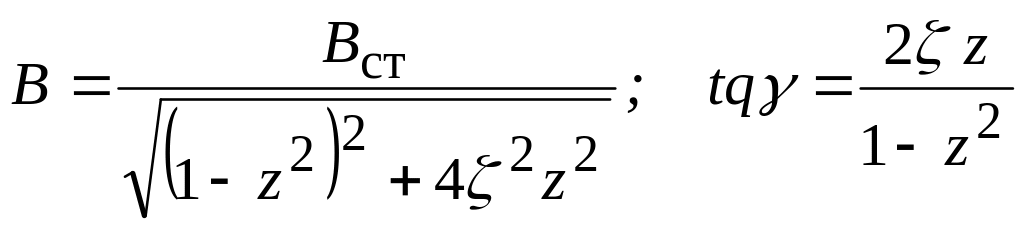. (4.154)

Вираз амплітуди В можна інакше записати так:

. (4.155)

Коефіцієнт називають коефіцієнтом динамічності системи, – коефіцієнтом розладу частот, – коефіцієнтом згасання.

Дослідимо функції і .

1. . Очевидно, максимуму відповідає мінімум підкореневого виразу (4.155). Позначимо його і розглянемо цю функцію

(4.156)

Визначимо її екстремуми.

Маємо:

або ,

звідки

; (4.157)

. (4.158)

На підставі (4.157) і (4.158) очевидно, що екстремум є мінімумом, і що він існує, якщо

.

Таким чином, при наявності сил опору амплітуда вимушених коливань необмеженою стати не може. При відсутності опору резонанс § 3.1.2 буде при 1, тобто при рівності частот вільних коливань і збурювальної сили. На підставі (4.157) зауважимо, що максимум амплітуди зсунуто ліворуч відносно точки резонансу (рис. 4.23). При наближенні до амплітуда вимушених коливань зростає, і це зростання залежить від .

Рисунок 4.23

О

Рисунок 4.24

бласть швидкого зростання амплітуд називають зоною резонансу.

2

6

. Розглянемо зсув фази , використовуючи формулу

.

П

3,0 Z

ри резонансі ( ) . Якщо = 0, = 0; при необмеженому зростанні . Закон зміни від і зображений на рис. 4.24.

Зауважимо, що збурювальна сила може мати вигляд довільної функції часу. Якщо ця функція задовольняє умовам Діріхле, то її можна розкласти в ряд Фурьє і знову скористатись розглянутим розв’язком.

Приклади

Приклад 4.4. Два однакових маятники довжиною і масою з’єднані на рівні пружиною жорсткістю (рис. 4.25). Одному з маятників надано відхилення на кут від положення рівноваги; початкові швидкості маятників дорівнюють нулеві. Нехтуючи масами стержнів і пружини, а також розмірами кульок, визначити малі коливання системи.

Розв’язання. Кількість степенів вільності системи дорівнює двом. Узагальненими координатами вважатимемо кути і . Сили, під дією яких відбувається рух – консервативні. Це сили ваги кульок і пружності пружини. У загальному вигляді рівняння руху цієї системи такі:

. (4.159)

Обчислимо функції і :

Рисунок 4.25

; (4.160)

.

де – деформація пружини,

.

Задовольняючи умову малості коливань, перетворимо вирази :

.

Аналогічно

.

Тоді

. (4.161)

Підставимо і до рівняння (4.159)

;

.

Рівняння (4.159) руху системи набувають вигляду:

;

(4.162)

.

Функції і визначимо у вигляді

;

(4.163)

.

Складемо рівняння частот:

(4.164)

або

. (4.165)

Перепишемо це рівняння у вигляді

(4.166)

і знайдемо його корені:

, (4.167)

де і – головні частоти коливань системи.

Визначимо амплітуди. На підставі (4.162) і (4.163) маємо алгебраїчне рівняння:

. (4.168)

з якого знаходимо

.

Для двох коренів і , визначених формулами (4.167), дістанемо

.

Отже, загальний розв’язок диференціальних рівнянь руху такий:

(4.169)

Інакше

(4.170)

Для визначення сталих інтегрування , знайдемо похідні від виразів (4.170)

Сталі інтегрування і знаходимо з початкових умов ( = 0):

(4.171)

Підставляючи початкові умови (4.171) до загального розв’язку (4.170) і до похідних і , дістаємо:

.

Остаточно знаходимо закон руху системи:

П

Рисунок 4.26

риклад 4.5. Астатичний маятник довжиною і масою , затиснутий двома горизонтальними пружинами жорсткості с на рівні а від опори (рис. 4.26). Нехтуючи масою стержня, визначити умову, за якою вертикальне положення рівноваги маятника буде стійким і знайти період малих коливань системи.

Розв’язання. Система має одну степінь вільності. Узагальнена координата – кут . Сили, що діють на систему, консервативні, тому рівняння руху має вигляд

. (4.172)

Обчислимо функції і Як і в попередньому випадку

; (4.173)

.

(4.174)

Перетворення, аналогічні наведеним у попередньому прикладі, дають змогу (4.174) записати у вигляді:

. (4.175)

Умову стійкості рівноваги (мінімуму потенціальної енергії) визначимо, застосувавши теорему Лагранжа-Діріхле:

;

. (4.176)

Це і є умова стійкості рівноваги системи. З неї знаходимо залежність між параметрами системи

.

Для визначення періоду коливань складемо рівняння руху системи за виразом (4.172). З (4.173) і (4.175) маємо

.

Отже, рівняння руху маятника має вигляд

.

Період коливань обчислимо за формулою

.

У даному випадку – частота коливань дорівнює

.

Період коливань

.