Сила f зчеплення з площиною у ньютонах

Рисунок 3.58

2. Знайдемо межі зміни прискорення центра мас котка, за умови його кочення без ковзання

Продовження табл. 3.3

№ блоку	Текст програми	Пояснення
	> plot(aC(P), P=P1..P2, color=red, title="Прискорення центра мас в м/С2",style=line,thickness=3);	Побудова графіків: (рис. 3.58)

Прискорення центра мас в м/с2

Р, Н

Рисунок 3.59

3. Для граничних значень сили р знайдемо рівняння руху котка, якщо у початковий момент він перебував у стані спокою

Продовження табл. 3.3

№ блоку	Текст програми	Пояснення
9.	> a1:=evalf(subs(P=P1,aC)): a2:=evalf(subs(P=P2,aC)):sС1:=a1*t^2/2; phi1:=s1/R; sС2:=a2*t^2/2; phi2:=s2/R; Закони руху котка	Закони руху котка:

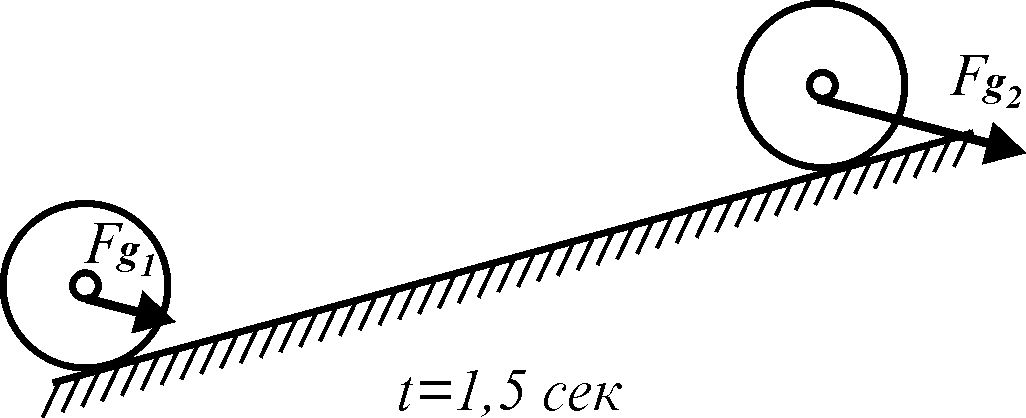
4. Змоделюємо рух котка для обох граничних випадків за отриманими законами руху

Продовження табл. 3.3

№ блоку	Текст програми	Пояснення
10.	Моделювання руху котка Параметри, що не залежать від часу y[1]:=R: a1:=evalf(subs(P=P1,aC)): a2:=evalf(subs(P=P2,aC)): p1:=evalf(P1/100): p2:=evalf(P2/1000):	Моделювання руху котка ордината центра котка, прискорення центра котка при граничних значеннях сили
11.	with(plots):with(plottools): arw:=0.05,0.15,0.3,color=red: Кількість кадрів K > T:=1.5: K:=72: Створюємо кадри руху for i from 0 to K do t:=i*T/K: Шрифт:=FONT(TIMES,ITALIC,20): Закони руху котка s1:=a1*t^2/2: phi1:=s1/R: Координати рухомих точок x[1]:= s1: x[2]:=r*sin(beta-phi1)+s1: y[2]:=R+r*cos(beta-phi1): x[3]:=x[2]+p1*cos(beta): y[3]:=y[2]-p1*sin(beta): Підписи тіл на рисунку F1:=arrow([x[2],y[2]],[x[3],y[3]],arw): T1:=PLOT(TEXT([x[3]-0.25,y[3]+0.4], 'Fg1'),Шрифт,COLOR(HUE,0)): P1[i]:=display(Cir(1,r),Cir(1,R),Рухоме_колесо(1,r,phi1), Рухоме_колесо (1,R,phi1), F1,T1):od:	параметри векторів, кінцевий час, кількість кадрів, закони руху котка, координати точок: абсциса центра котка, координати початку вектора сили , координати кінця вектора сили , вектор , підпис сили
12.	Зображення котка у русі PP1:=display(seq(P1[i],i=0..K), insequence=true, thickness=2, scaling= constrained, axes=none):	Зображення котка на дисплеї комп’ютера

Рекомендації щодо написання програми для дослідження плоскопаралельного руху тіла (див. табл. 3.3).

Блок 1 є обов’язковим для будь-якої програми, а підпрограма, що використовується у блоці 2 вже змодельована на кафедрі теоретичної механіки і студент може її взяти у готовому вигляді.

Примітка: у готовій підпрограмі при бажанні можна змінювати тільки кольори графічних об’єктів в операторі .

У блоці:

• студент вводить параметри котка згідно виданому завданню (табл. 3.3);

• необхідно ввести диференціальні рівняння руху котка;

• з рівнянь (3.233) визначають реакцію , силу зчеплення , прискорення центра котка як функцію зовнішньої сили ;

• будують графіки залежності , , на проміжку ;

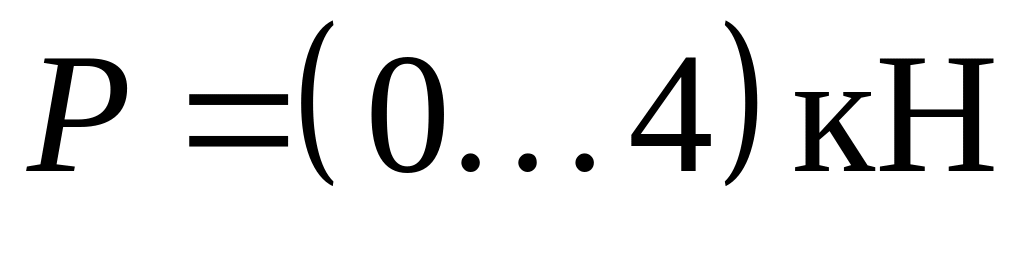• виводять на друк значення зовнішньої сили, при яких коток котиться без ковзання;

• будують графік залежності прискорення центра мас котка для тих значень сили , при яких кочення відбувається без ковзання;

• виводять на друк закони руху котка при граничних значеннях сили ;

• моделювання руху котка розпочинають з введення параметрів, що не залежать від часу;

• вводять параметри; що змінюються з часом;

• виводять зображення котка на дисплей комп’ютера.

У результаті спостерігаємо на екрані дисплея ком-п’ютера рух котка при граничних значеннях сили (рис. 3.60).

Рисунок  3.60

РОЗДІЛ 4

ЕЛЕМЕНТИ АНАЛІТИЧНОЇ МЕХАНІКИ

4.1. Диференціальні принципи механіки

4.1.1. Основні положення

Диференціальні принципи аналітичної механіки визначають закономірності руху системи точок за досить малий проміжок часу. В аналітичній механіці Лагранжа є два диференціальних принципи: принцип можливих переміщень (Лагранжа) і принцип Даламбера-Лагранжа.

Принцип можливих переміщень є наслідком визначення можливих переміщень і деяких властивостей в’язей.

Поняття про малі переміщення належить до найважливіших понять аналітичної механіки. Відрізнятимемо можливі, здійснені та дійсні переміщення.

Можливими називають малі переміщення, що дозволяються в’язями в певний фіксований момент часу.

Ці поняття кінематичні і уявні, тобто вони ніяк не пов’язані з силами, діючими на точки системи. При наданні точкам системи можливих переміщень нестаціонарні в’язі необхідно вважати “зупиненими”, а час фіксованим.

Здійсненими переміщеннями називають переходи точок системи з одного положення в просторі і в часі в інші, які дозволяють в’язі. Час при цьому не фіксується, нестаціонарні в’язі не “зупиняються”.

Дійсні переміщення відповідають справжньому закону руху системи і відбуваються під дією сил, прикладених до точок системи. Ці переміщення утворюють одну із систем здійснених переміщень.

У загальному випадку можливі і здійсненні переміщення не можуть збігатися. Але якщо в’язі, накладені на точки системи, стаціонарні, то можливі і здійсненні переміщення можуть збігатися. У цьому випадку дійсні переміщення утворюють одну з систем можливих переміщень.

Тут і далі позначатимемо вектор можливого переміщення , здійсненого , дійсного .

З’ясуємо деякі властивості в’язей. У § 3.2.1 дано аналітичне визначення в’язей і розглянуто окремий випадок – поняття ідеальних в’язей. Розглянемо властивості ідеальних в’язей, звернувшись до найпоширеніших прикладів в’язей: поверхня, стержень, трос.

Н

Рисунок 4.1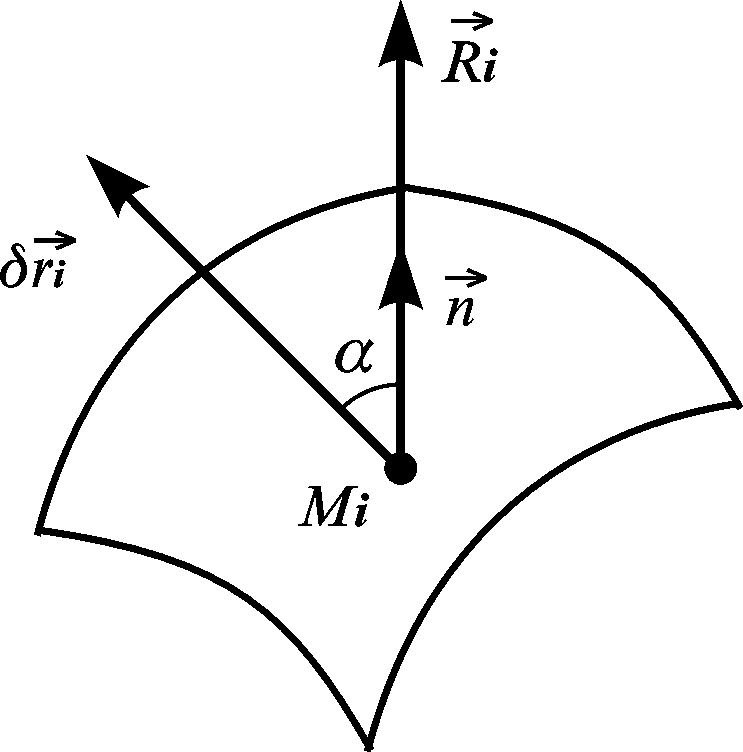

ехай точки знаходяться на ідеально гладенькій поверхні (рис. 4.1). Реакція такої в’язі збігається з нормаллю до поверхні. Надамо точці можливого переміщення . Вектор напрямлений по дотичній до поверхні, якщо точка залишається на ній , і утворює гострий кут з нормаллю, якщо точка покидає поверхню , тобто .

В’язь, яку точка може покинути, називають неутримувальною, або однобічною.

Обчислимо елементарну роботу , яку виконує реакція в’язі на можливому переміщенні :

. (4.1)

Якщо на поверхні знаходиться система точок, то вираз (4.1) набуває вигляду

(4.2)

Знак нерівності відповідає випадку, коли точки покидають в’язь.

Розглянемо приклад утримувальної в’язі – абсолютно твердий стержень, що з’єднує дві матеріальні точки (рис. 4.2).

Надамо точкам можливих переміщень і і обчислимо елементарну роботу реакцій і на цих переміщеннях. Для цього скористаємося теоремою про роботу сил, що діють на абсолютно тверде тіло. Внаслідок того, що сили і рівні за модулем і протилежні за напрямом, їх головний вектор і головний момент дорівнюють нулеві.

. (4.3)

Рисунок 4.2

Поверхня – однобічна в’язь, тому , стержень – двобічна, тому . Узагальнимо отримані результати.

Сума робіт реакцій ідеальних в’язей на можливих переміщеннях точок системи – величина додатна або рівна нулеві:

. (4.4)

Знак нерівності у виразі (4.4) відповідає наявності однобічних в’язей і таких можливих переміщень, що звільняють точки системи від цих в’язей.