
- •Передмова
- •1.1.2. Означення статики
- •1.1.3. Механічні в’язі та їхні реакції
- •В’язь – гладенька поверхня
- •Гостре вістря або ребро
- •В’язь – шорстка поверхня
- •В’язь – невагома, нерозтяжна ідеальна нитка
- •В’язь – стержень
- •В’язь – нерухома шарнірна опора
- •В’язь – жорстке защемлення (заробка)
- •1.1.4. Аксіоми про в’язі та їхні реакції
- •1.1.5. Класифікація сил. Метод перерізів
- •1.1.6. Теорема про рівновагу трьох непаралельних сил, прикладених до твердого тіла
- •1.1.7. Сили тертя ковзання і їхні властивості
- •Запитання для самоконтролю
- •1.2. Основні властивості систем сил, прикладених до абсолютно твердого тіла
- •1.2.1. Аналітичне визначення ковзного вектора.
- •1.2.2. Система збіжних сил. Умови рівноваги
- •Задачі для самостійного розв’язування
- •1.2.3. Аналітичне визначення ковзного вектора рівнодійної системи двох паралельних сил. Центр паралельних сил
- •1.2.4. Пара сил. Момент пари сил. Властивості пар сил
- •Запитання для самоконтролю
- •1.3. Перетворення систем сил. Умови рівноваги
- •1.3.1. Аналітичне визначення головного вектора і головного моменту системи сил
- •1.3.2. Умови рівноваги вільного твердого тіла
- •Задачі для самостійного розв’язування
- •1.3.3. Зведення систем сил до найпростішого вигляду. Інваріанти системи сил відносно центра зведення
- •2. Якщо ; , то система сил зводиться до пари сил.
- •3. Якщо і – система зрівноважується.
- •1.3.4. Центр паралельних сил і центр ваги
- •1.4. Розрахунково-графічна робота із застосуванням комп’ютера
- •Завдання на розрахунково-графічнУ роботУ
- •Ферма з позначеними силовими зонами
- •Діаграма Максвелла-Кремони
- •На діаграмі зображено:
- •2.1.2. Способи визначення руху точки
- •2.1.3. Годограф векторної функції
- •2.1.4. Швидкість руху точки
- •2.1.5. Прискорення руху точки
- •Приклади
- •Задачі для самостійного розв’язування
- •Запитання для самоконтролю
- •2.2. Кінематика абсолютно твердого тіла
- •2.2.1. Основні положення
- •2.2.2. Поступальний рух твердого тіла
- •2.2.3. Обертальний рух твердого тіла навколо нерухомої осі
- •Координати точки м і орт не залежать від часу; орти , є функціями часу. Отже,
- •Приклади
- •Задачі для самостійного розв’язування
- •Запитання для самоконтролю
- •2.2.6. Плоскопаралельний рух твердого тіла. Рівняння руху
- •2.2.7. Розподіл швидкостей точок тіла при плоскопаралельному русі
- •2.2.8. План швидкостей
- •2.2.10. Миттєвий центр прискорень
- •Приклади
- •Задачі для самостійного розв’язування
- •Запитання для самоконтролю
- •2.2.11. Додавання обертальних рухів тіла навколо осей, що перетинаються
- •Аксоїди. Теорема Пуансо
- •2.2.13. Теорема Ейлера. Кути Ейлера. Рівняння руху твердого тіла з нерухомою точкою
- •2.2.14. Розподіл швидкостей і прискорень точок тіла з нерухомою точкою
- •Задачі для самостійного розв’язування
- •2.3. Складний рух матеріальної точки
- •2.3.1. Основні положення
- •2.3.2. Теорема про додавання швидкостей точки
- •2.3.3. Теорема про додавання прискорень точки
- •2.4. Складний рух твердого тіла
- •2.4.1. Додавання поступальних рухів тіла
- •2.4.2. Пара обертань
- •2.4.3. Додавання обертань тіла навколо паралельних осей
- •2.4.4. Додавання поступального і обертального рухів тіла
- •2.4.5. Метод “зупинки” (метод Вілліса)
- •Задачі для самостійного розв’язування
- •2.5. Розрахунково-графічна робота із застосуванням комп’ютера
- •Завдання на розрахунково-графічнУ роботУ
- •1. Спроектувати за допомогою комп’ютера механізм, при цьому зобразити ланки, які здійснюють:
- •2. Роздрукувати механізм для заданого положення кута та для трьох положень кута 60, 120, 240.
- •3. Зобразити кутові швидкості всіх ланок та вектори швидкостей усіх точок механізму, вказавши положення миттєвих центрів швидкостей (рис. 2.76 – 2.78)
- •4. Побудувати план швидкостей (рис. 2.76 - 2.78)
- •5. Зобразити кутові прискорення всіх ланок та вектори прискорень усіх точок механізму за допомогою плану прискорень (рис. 2.79–2.81)
- •2.6 Знайти положення миттєвих центрів прискорень
- •Розділ 3 динаміка
- •3.1. Динаміка матеріальної точки
- •3.1.1. Диференціальні рівняння руху вільної матеріальної точки. Основні задачі динаміки точки
- •3.1.2. Прямолінійні коливання точки
- •Задачі для самостійного розв’язування
- •Запитання для самоконтролю
- •3.2. Динаміка системи матеріальних точок
- •3.2.1. Основні поняття
- •3.2.2. Диференціальні рівняння руху невільної системи
- •3.2.3. Принцип Даламбера
- •3.2.4. Динаміка відносного руху точки
- •Задачі для самостійного розв’язування
- •Запитання для самоконтролю
- •3.3. Основні теореми динаміки
- •3.3.1. Теорема про зміну кінетичної енергії точки
- •Приклади
- •3.3.2. Елементи теорії потенціального силового поля. Закон збереження повної механічної енергії
- •3.3.3. Теорема про зміну кінетичної енергії матеріальної системи
- •3.3.4. Обчислення моментів інерції
- •3.3.5. Теорема про рух центра мас системи
- •3.3.6. Теореми про зміну кількості руху системи і зміну кінетичного моменту
- •Приклади
- •Задачі для самостійного розв’язування
- •Запитання для самоконтролю
- •3.4. Елементи теорії удару
- •Співудар двох куль
- •Теорема Остроградського-Карно (про зміну кінетичної енергії при ударі)
- •Фізичний маятник під дією удару
- •Приклади
- •3.5. Розрахунково-графічна робота із застосуванням комп’ютера
- •Завдання на розрахунково-графічнУ роботУ
- •Завдання
- •1. Визначимо значення сили , за яких кочення відбувається без ковзання, а також її граничні значення, коли зчеплення котка з дорогою знаходиться на межі зриву
- •Сила f зчеплення з площиною у ньютонах
- •2. Знайдемо межі зміни прискорення центра мас котка, за умови його кочення без ковзання
- •Прискорення центра мас в м/с2
- •3. Для граничних значень сили р знайдемо рівняння руху котка, якщо у початковий момент він перебував у стані спокою
- •4. Змоделюємо рух котка для обох граничних випадків за отриманими законами руху
- •4.1.2. Принцип можливих переміщень. Загальне рівняння статики
- •4.1.3. Принцип Даламбера-Лагранжа. Загальне рівняння динаміки
- •Приклади
- •Задачі для самостійного розв’язування
- •Запитання для самоконтролю
- •4.2.2. Загальне рівняння статики в узагальнених координатах. Узагальнені рівняння рівноваги
- •4.2.3. Рівняння Лагранжа другого роду
- •4.2.4. Методика застосування рівнянь Лагранжа другого роду
- •1. Диференціальне рівняння обертального руху твердого тіла навколо нерухомої осі
- •2 Диференціальні рівняння плоскопаралельного руху твердого тіла
- •4.2.5 Рух системи в консервативному полі. Кінетичний потенціал
- •4.2.6. Рівняння Лагранжа другого роду для дисипативних систем. Функція Релея
- •4.2.7. Кінетична енергія і функція Релея в узагальнених координатах
- •4.2.8. Узагальнене рівняння енергії. Фізичний зміст функції Релея
- •Задачі для самостійного розв’язування
- •Запитання для самоконтролю
- •4.3. Малі коливання матеріальної системи
- •4.3.1. Положення стійкої рівноваги. Теорема Лагранжа-Діріхле і теореми Ляпунова
- •4.3.2. Диференціальні рівняння малих коливань системи в околі положення стійкої рівноваги
- •4.3.3. Вільні коливання системи з степенями вільності
- •4.3.4. Вільні коливання системи з одним степенем вільності. Інтерпретація руху на фазовій площині
- •4.3.5. Вплив сил опору на вільні коливання системи. Згасаючі коливання
- •4.3.6. Вимушені коливання системи. Вплив сил опору на вимушені коливання
- •4.3.7. Дослідження амплітудно-частотних характеристик системи
- •Приклади
- •Задачі для самостійного розв’язування
- •Запитання для самоконтролю
- •1. Складемо рівняння Лагранжа іі роду
- •3. Визначимо натяги у нитках, до яких прикріплені вантажі 1 і 4;
- •4. Змоделюємо рух механічної системи з отриманими законами руху.
- •Завдання на розрахунково-графічнУ роботУ
- •Завдання
- •1. Складемо рівняння Лагранжа іі роду
- •Знайдемо власні частоти коливань.
- •3. Визначимо закони руху еліптичного маятника.
- •4. Змоделювати рух еліптичного маятника за отриманими законами руху.
- •Список літератури
- •А українсько-російський словник
- •Предметний покажчик
3.3.3. Теорема про зміну кінетичної енергії матеріальної системи
Кінетична енергія Т системи дорівнює сумі кінетичних енергій точок, які складають систему:
![]() .
(3.117)
.
(3.117)
Якщо до кожної точки застосувати теорему про зміну кінетичної енергії, то дістанемо рівність
![]() ,
,
де
![]() — повна робота всіх зовнішніх і внутрішніх
сил, прикладених до цієї точки. Додавши
рівності по всіх і,
дістанемо
— повна робота всіх зовнішніх і внутрішніх
сил, прикладених до цієї точки. Додавши
рівності по всіх і,
дістанемо
![]() ,
,
або
![]() .
(3.118)
.
(3.118)
Приріст кінетичної енергії системи за певний проміжок часу дорівнює роботі всіх (внутрішніх і зовнішніх) сил, прикладених до точок системи, виконаній за той самий проміжок часу.
Це твердження є змістом теореми про зміну кінетичної енергії системи.
Одна з особливостей цієї теореми – що в ній ураховується робота внутрішніх сил. Звичайно головний вектор і головний момент внутрішніх сил дорівнюють нулеві, але робота, виконана ними, може відрізнятися від нуля. Наприклад, система складається з двох точок, сили їх взаємодії є силами тяжіння. Нехай одна точка нерухома, а друга наближається до першої. Головний вектор внутрішніх сил дорівнює нулеві, робота сили, яка прикладена до першої (нерухомої) точки, дорівнює нулеві, а робота другої сили відмінна від нуля.
Зрозуміло, що
при незмінній системі робота внутрішніх сил дорівнює нулеві.
Доведена теорема – частинний випадок більш загальної теореми про зміну та збереження енергії. Зокрема,
робота є мірою тієї частини кінетичної енергії, яка або виникла з інших форм енергії, або перетворилася в інші форми.
При застосуванні теореми (3.118) до конкретних задач потрібно навчитись обчислювати як кінетичну енергію системи та твердого тіла, так і роботу. |
Якщо
система є певним об’ємом
суцільного середовища, то розкладемо
його на
елементів з масами
![]() ;
швидкість певної внутрішньої точки
елемента дорівнює
;
швидкість певної внутрішньої точки
елемента дорівнює
![]() .
На підставі (3.117) приблизно обчислимо
кінетичну енергію вказаного об’єму
.
На підставі (3.117) приблизно обчислимо
кінетичну енергію вказаного об’єму
![]() .
.
Точне
значення кінетичної енергії дістанемо
після граничного переходу, якщо
![]() при
при
![]() .
Таким чином, кінетична
енергія суцільного середовища,
зокрема абсолютно твердого тіла, дорівнює
.
Таким чином, кінетична
енергія суцільного середовища,
зокрема абсолютно твердого тіла, дорівнює
![]() ,
(3.119)
,
(3.119)
де — маса тіла.
Розглянемо окремі випадки обчислення кінетичної енергії для різних видів руху.
Випадок 1. Якщо тіло рухається поступально, то швидкості всіх його точок однакові і дорівнюють швидкості центра мас . Отже, кінетична енергія тіла, яке рухається поступально,
![]() ,
(3.120)
,
(3.120)
тобто обчислюється як кінетична енергія точки, маса якої дорівнює масі системи.
Випадок 2. Обчислимо кінетичну енергію тіла, яке має нерухому точку.
Розподіл
швидкостей відповідає формулі Ейлера
![]() ,
а проекції швидкості на осі координат,
початок яких збігається з нерухомою
точкою,
,
а проекції швидкості на осі координат,
початок яких збігається з нерухомою
точкою,

На підставі (3.119)
![]()
![]() ;
(3.121)
;
(3.121)
![]()
![]() .
(3.122)
.
(3.122)
Інтеграли, які входять до перших трьох доданків, називають осьовими моментами інерції:
![]()
![]() (3.123)
(3.123)
Величини, визначені формулами (3.123), називають відцентровими моментами інерції.
На підставі (3.121), (3.122) і (3.123) вираз кінетичної енергії набуває вигляду
![]()
(3.124)
![]() .
.
Випадок
3.
Якщо тіло
обертається навколо нерухомої осі,
наприклад, осі
,
то
![]() ,
і кінетична енергія тіла
,
і кінетична енергія тіла
![]() .
(3.125)
.
(3.125)
Порівнюючи вирази (3.120) і (3.125), можна визначити, що
момент інерції відносно осі – фізична величина, яка характеризує властивості інерції тіла при його обертанні навколо осі.
Обчислимо кінетичну енергію системи в її довільному русі.
Кожна
точка системи здійснює складний рух,
швидкість якого складається з переносної
і відносної швидкостей. Нехай переносний
рух буде поступальним зі швидкістю, яка
дорівнює швидкості центра мас системи
![]() .
Тоді абсолютна швидкість точки
.
Тоді абсолютна швидкість точки
![]() .
.
де
![]() – відносна швидкість точки.
– відносна швидкість точки.
Цей вираз підставимо в (3.117)
![]()
 .
.
Останній член дорівнює нулеві на підставі формул (3.62) і (3.65)
![]() ,
,
оскільки
![]() – це відносна швидкість центра мас
відносно самого себе. Остаточно знайдемо
– це відносна швидкість центра мас
відносно самого себе. Остаточно знайдемо
![]() .
(3.126)
.
(3.126)
На підставі (3.126) сформулюємо теорему (вона назива- ється теоремою Кеніга):
кінетична енергія системи дорівнює кінетичній енергії поступального руху системи разом із центром мас і кінетичній енергії точок системи при їх русі відносно центра мас.
Рухом точок відносно центра мас називають їх рух відносно системи координат з початком у центрі мас, яка рухається поступально.
Випадок
4.
При плоскопаралельному
русі твердого тіла
відносна швидкість
![]() точок є швидкістю обертального руху
навколо центра мас, яка дорівнює
точок є швидкістю обертального руху
навколо центра мас, яка дорівнює
![]() .
Отже, на підставі (3.126) знайдемо кінетичну
енергію твердого тіла при плоскопаралельному
русі
.
Отже, на підставі (3.126) знайдемо кінетичну
енергію твердого тіла при плоскопаралельному
русі
![]() ,
(3.127)
,
(3.127)
де
![]() – момент інерції тіла відносно осі, яка
проходить перпендикулярно до площини,
у якій відбувається плоскопара-лельний
рух, через центр мас тіла. Цю вісь
називають
центральною.
– момент інерції тіла відносно осі, яка
проходить перпендикулярно до площини,
у якій відбувається плоскопара-лельний
рух, через центр мас тіла. Цю вісь
називають
центральною.
Випадок 5. Якщо у (3.126) замість останнього члена в правій частині поставити (3.124), то дістанемо вираз кінетичної енергії вільного твердого тіла.
Оскільки рух навколо нерухомої точки можна розглядати як рух навколо миттєвої осі, яка проходить через нерухому точку, то кінетичній енергії вільного тіла можна надати вигляду
![]() ,
(3.128)
,
(3.128)
де
![]() – момент інерції тіла відносно миттєвої
осі, яка змінює з часом свій напрям.
– момент інерції тіла відносно миттєвої
осі, яка змінює з часом свій напрям.
Обчислимо роботу сил, які прикладені до абсолютно твердого тіла.
Точка
О
– його полюс, точка
нерухома. Розглянемо роботу сили
![]() (рис. 3.30):
(рис. 3.30):
![]() .
(3.129)
.
(3.129)
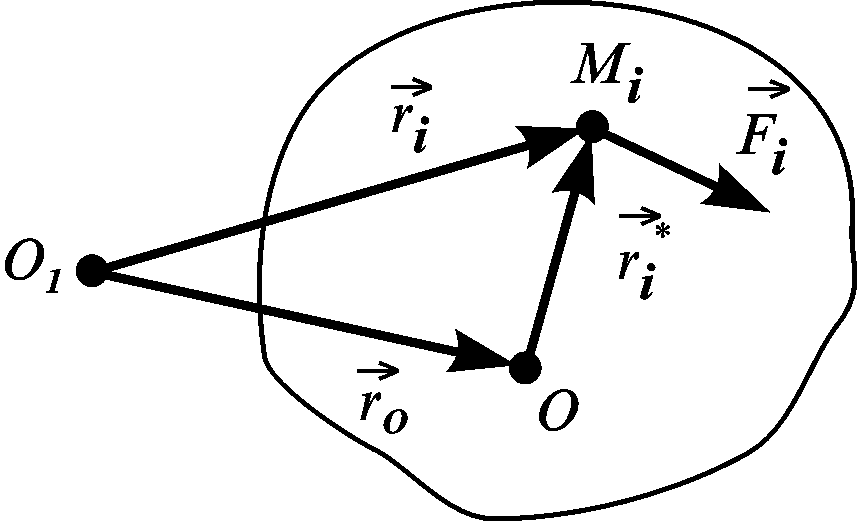
Рисунок 3.30
Проведемо
радіуси-вектори точки
![]() і
і
![]() ,
причому
,
причому
![]() .
.
Диференціюючи цей вираз, дістаємо
![]() .
.
Швидкість довільної точки твердого тіла
![]() ,
,
або
![]() .
.
Помножимо ліву й праву частини цієї рівності на :
![]() .
.
Позначимо
добуток
![]() через
через
![]() ,
який називають елементарним
кутом обертання
тіла навколо осі, що проходить через
полюс.
,
який називають елементарним
кутом обертання
тіла навколо осі, що проходить через
полюс.
Отже, для твердого тіла виконується рівність
![]() .
(3.130)
.
(3.130)
На підставі (3.130) обчислимо елементарну роботу (3.129)
![]() ,
,
або
![]() .
(3.131)
.
(3.131)
Вираз (3.131) є наслідком циклічної перестановки множників у скалярно-векторному добутку.
Елементарна робота всіх сил, прикладених до твердого тіла, дорівнює алгебраїчній сумі елементарних робіт сил:
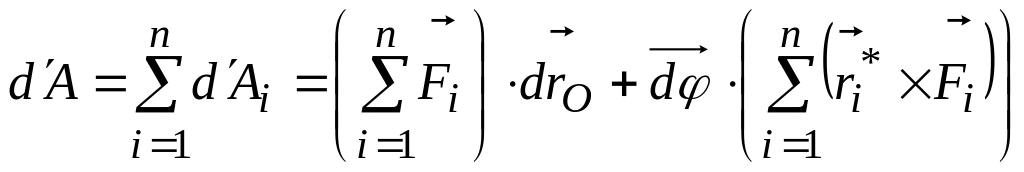 .(3.132)
.(3.132)
Тут
![]() та
та
![]() винесено за знак суми, оскільки вони
однакові для всіх точок.
винесено за знак суми, оскільки вони
однакові для всіх точок.
Але
![]() ,
тобто дорівнює головному вектору системи
сил, а
,
тобто дорівнює головному вектору системи
сил, а
![]() ,
тобто дорівнює головному моменту системи
сил відносно полюса О.
,
тобто дорівнює головному моменту системи
сил відносно полюса О.
Таким чином,
![]() ,
(3.133)
,
(3.133)
тобто
елементарна робота сил, прикладених до абсолютно твердого тіла, дорівнює роботі, яку виконує головний вектор системи сил на переміщенні полюса, і роботі головного моменту системи сил відносно полюса на обертальному переміщенні навколо осі, яка проходить через полюс.
Якщо
тіло рухається поступально,
то
![]()
![]() ,
,
Якщо
тіло обертається
навколо нерухомої осі,
то
![]() і
і
![]() .
.
Покажемо, що робота внутрішніх сил, прикладених до точок абсолютно твердого тіла, дорівнює нулеві.
Дійсно, з (3.133)
![]()
оскільки
![]() за третім законом Ньютона, то
за третім законом Ньютона, то
![]() .
.
Примітка. При малій кількості годин, відведених на вивчення теоретичної механіки, поняття про головний вектор і головний момент можна запровадити саме тут і далі дістати рівняння рівноваги таким способом.
Означення. Абсолютно тверде тіло перебуває в рівновазі, якщо його кінетична енергія не змінюється, або дорівнює нулеві.
На підставі теореми про зміну кінетичної енергії системи (3.118), яку подамо в диференціальній формі, і наведеного означення стану рівноваги можна написати
![]() .
(3.134)
.
(3.134)
Але згідно з теоремою про обчислення роботи сил, прикладених до абсолютно твердого тіла, маємо
![]() .
(3.135)
.
(3.135)
Достатньою умовою виконання рівності нулеві цього виразу буде рівність одночасно нулеві головного вектора і головного моменту системи сил, які прикладені до твердого тіла
![]() .
(3.136)
.
(3.136)
Доведемо необхідність цих умов для рівноваги.
Оскільки
поступальне переміщення
тіла і обертальне
навколо полюса незалежні одне від
одного, то можна спочатку припустити,
що
![]() ;
а
;
а
![]() .
У цьому разі тіло рухається поступально.
Тоді на підставі (3.135) при рівновазі тіла
виконується рівність
.
У цьому разі тіло рухається поступально.
Тоді на підставі (3.135) при рівновазі тіла
виконується рівність
![]() ,
,
але
.
Отже, необхідно, щоб
![]() .
.
Припустимо,
що
![]() ,
тобто тіло обертається навколо осі.
,
тобто тіло обертається навколо осі.
Згідно з (3.135)
![]() .
.
Оскільки
![]() ,
то
,
то
![]() .
.
Таким чином, дістали фізичні умови рівноваги (1.38) твердого тіла.
