3.3. Основні теореми динаміки

Досить часто при інтегруванні диференціальних рівнянь руху виникають труднощі математичного характеру, які перешкоджають безпосередньо визначати закони руху.

Але в певних випадках залежно від умов задач механіки можна безпосередньо знайти перші інтеграли диференціальних рівнянь руху при досить загальних припущеннях.

Ці випадки розглядаються в загальних теоремах динаміки, які всі є висновками з другого закону І.Ньютона, але кожна теорема підкреслює фізичний зміст певних умов задачі.

Існують чотири основні теореми динаміки: про рух центра мас системи; про зміну кількості руху; про зміну кінетичної енергії; про зміну кінетичного моменту.

3.3.1. Теорема про зміну кінетичної енергії точки

Припустимо, є матеріальна точка, рух якої описується диференціальним рівнянням

, (3.89)

де – рівнодійна сил, прикладених до точки.

Якщо точка невільна, то потрібно звільнити її від в’язей, реакції яких входять до сили .

Помножимо спочатку ліву й праву частини (3.89) ска- лярно на вектор швидкості , який дорівнює :

,

а потім – на :

. (3.90)

Зауваживши, що

,

дістанемо з (3.90)

. (3.91)

Ця рівність виражає теорему про зміну кінетичної енергії матеріальної точки в диференціальній формі.

Величину під назвою “жива сила” вперше запровадив Лейбніц, вважаючи, що вона може змінювати динамічну взаємодію тіл і що тільки вона, а не (міра Декарта), може бути мірою руху.

Вираз називають кінетичною енергією матеріальної точки.

Довгий час між прихильниками Лейбніца і Декарта точилася дискусія про те, що зберігається в природі — кількість руху чи жива сила. Але в ХVШ ст. вона не могла привести до будь-яких конкретних результатів, оскільки тільки в ХХ ст. з’ясувалося, що обидві міри поєднуються загальною мірою, спроможною вимірювати не тільки механічні рухи, а й ті, в які вони переходять. Цю міру називають тензором енергії – імпульсів.

Теорему (3.91) відкрив Гельмгольц понад сто років тому.

У правій частині (3.91) стоїть величина, яка впливає на зміну кінетичної енергії. Її називають елементарною роботою сили. Вона позначається

, (3.92)

д

Рисунок 3.21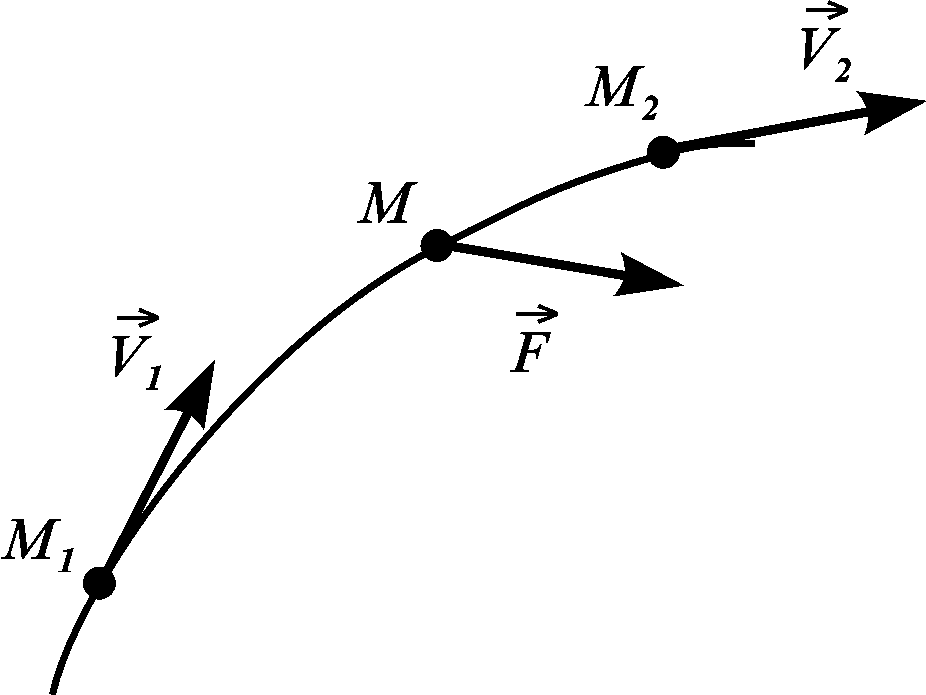

е штрих указує на те, що не завжди є повним диференціалом функції А.

Щоб знайти вираз згаданої теореми в закінченому вигляді, проінтегруємо вираз (3.91) у границях: ліву – від , до , праву – від до , де індексами “1” і “2” позначено відповідно початкове і кінцеве положення точки на її траєкторії (рис. 3.21).

Тоді матимемо

,

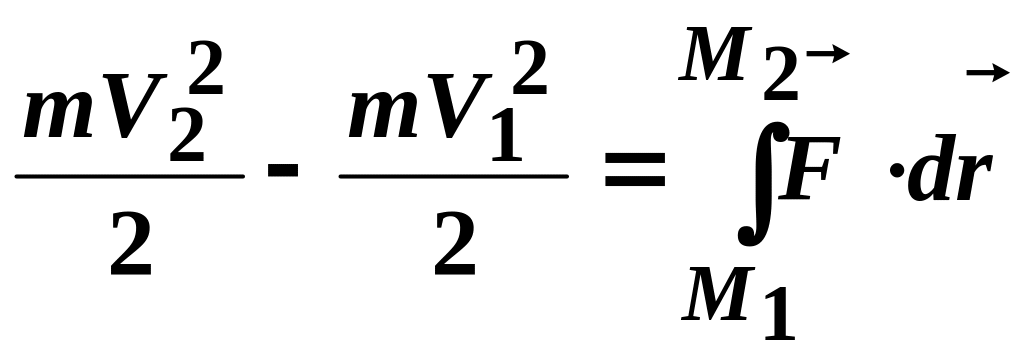де величину

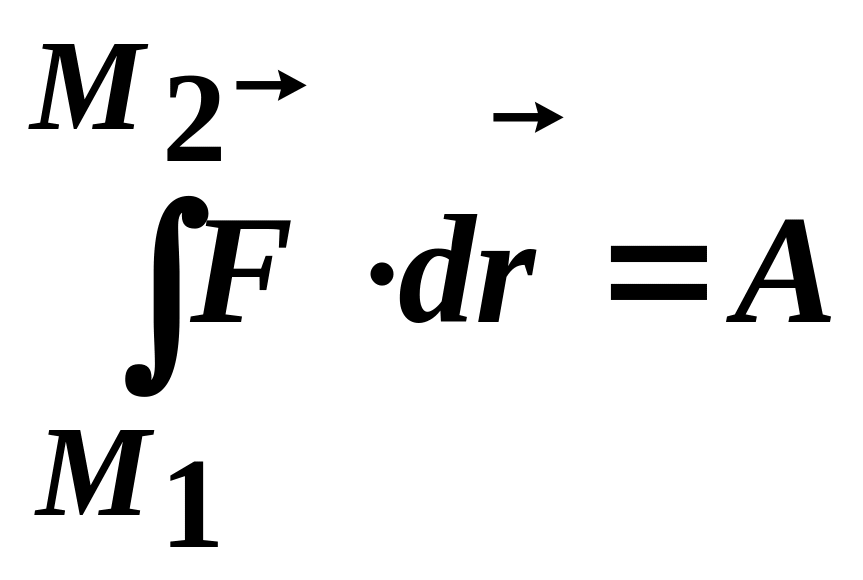(3.93)

називають повною роботою сили і позначають через А.

Отже,

, (3.94)

тобто

приріст кінетичної енергії точки на певному відрізку дуги її траєкторії дорівнює повній роботі, виконаній рівнодійною сил, прикладених до точки, на цьому самому відрізку траєкторії.

Для застосування цієї теореми потрібно навчитися обчислювати роботу конкретних сил та вивчити її властивості.

Розглянемо способи визначення роботи.

Вирази (3.92) і (3.93) визначають роботу сили у векторному вигляді.

При координатному способі визначення руху точки, вектор сили має проекції , а приріст радіуса-вектора

,

де – орти координатних осей. На підставі (3.92) скалярний добуток у координатній формі

. (3.95)

Цей вираз є елементарною роботою сили, а повна робота згідно (3.93) обчислюється за допомогою так званого криволінійного інтеграла

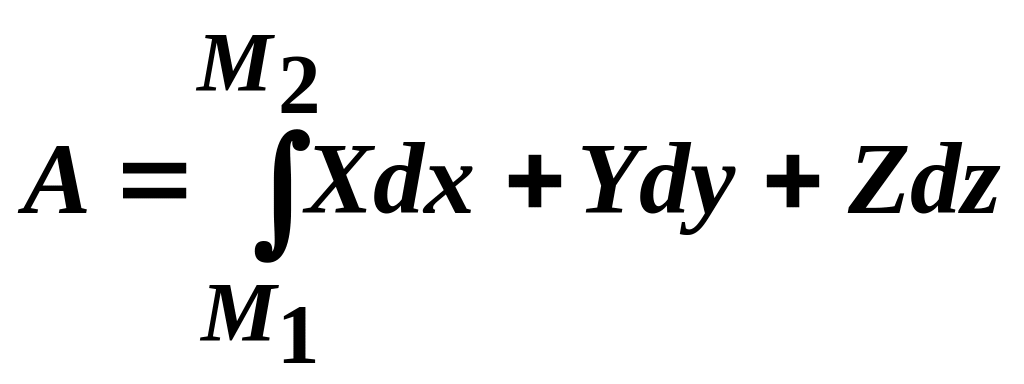(3.96)

в його нормальній формі.

Якщо застосувати натуральний спосіб, то на підставі означень кінематики точки орт дотичної до траєкторії

,

де – дугова координата.

Звідси , на підставі (3.92)

,

або, оскільки ,

. (3.97)

Повна робота

,

де .

Доведемо теорему про роботу рівнодійної.

Елементарна робота, яка виконана рівнодійною сил, дорівнює алгебраїчній сумі елементарних робіт складових сил, прикладених до точки.

За означенням (1.18) рівнодійна . Підставимо цей вираз у (3.92):

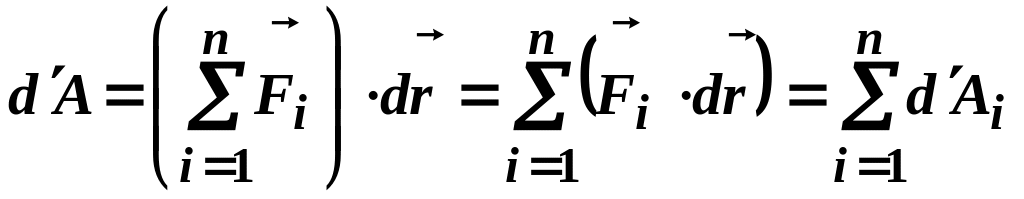. (3.98)

Цей висновок можна поширити на вираз повної роботи.