2.2. Кінематика абсолютно твердого тіла

2.2.1. Основні положення

Основне завдання кінематики твердого тіла – визначення закону руху і основних характеристик руху – швидкості та прискорення.

При вивченні руху твердого тіла розглядатимемо як характеристики руху всього тіла в цілому, так і характеристики руху окремих точок тіла.

Найпростішими рухами твердого тіла називають поступальний рух і обертальний рух навколо нерухомої осі. Далі покажемо, що будь-який рух можна розкласти на поступальний і обертальний навколо нерухомої осі.

2.2.2. Поступальний рух твердого тіла

Поступальним називають такий рух твердого тіла, при якому довільна пряма, проведена в тілі, рухається паралельно сама собі.

Для дослідження поступального руху твердого тіла доведемо теорему:

при поступальному русі твердого тіла траєкторії всіх його точок конгруентні і всі його точки рухається з однаковими швидкостями й прискореннями.

 Розглянемо в тілі дві довільні точки та і визначимо їхні рухи векторним способом:

; .

На підставі рис. 2.13 маємо:

. (2.38)

Функції і визначають векторним способом траєкторії точок та .

Вектор не змінюється за величиною і напрямом з часом. Отже, із (2.38) видно, що траєкторію точки можна дістати з траєкторії точки за допомогою паралельного переносу. Напрям і величину переносу визначає вектор .

Рисунок 2.13

Знайдемо похідну за часом від виразу (2.38)

.

Вектор , тому , тобто

. (2.39)

Диференціюючи (2.39) за часом , дістанемо

.  (2.40)

На підставі доведеної теореми можна стверджувати, що поступальний рух повністю визначається рухом однієї довільної точки тіла. Отже, вивчення поступального руху безпосередньо пов’язане з кінематикою точки.

2.2.3. Обертальний рух твердого тіла навколо нерухомої осі

Обертальним навколо нерухомої осі називають рух твердого тіла, при якому певна пряма (вісь обертання) залишається нерухомою.

Визначимо закон обертального руху тіла навколо нерухомої осі. Нехай вісь (рис. 2.14) є нерухомою віссю, навколо якої обертається тіло. Проведемо через вісь у деякий початковий момент часу площину . Через деякий проміжок часу ця площина займе положення , створивши двогранний кут зі своїм початковим положенням. Цей двогранний кут називають кутом повороту тіла і його вимірюють лінійним кутом в радіанах.

Вважатимемо кут повороту додатним, якщо з боку додатного напряму осі цей поворот видно проти ходу годинникової стрілки.

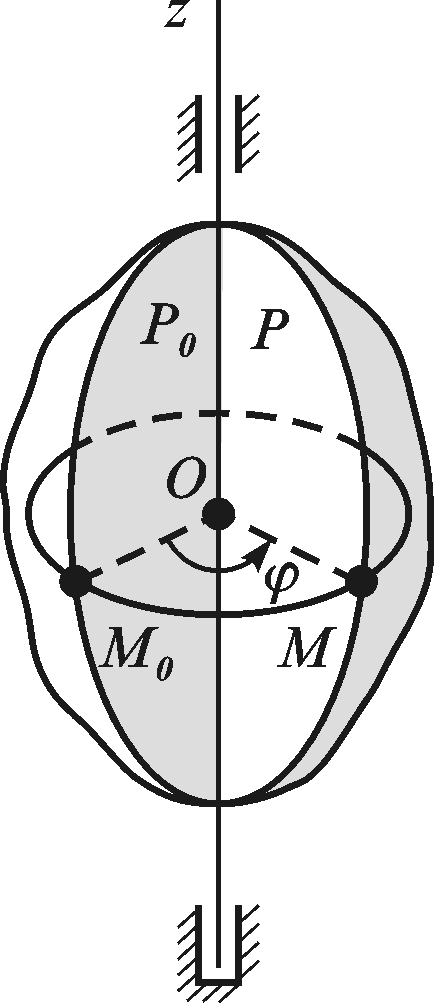
Рисунок 2.14

Кожному моменту часу відповідає певне значення кута повороту . Отже, кут повороту є функцією часу:

[рад]. (2.41)

Це рівняння визначає закон руху тіла, що обертається навколо нерухомої осі.

З кутом повороту пов’язані дві кінематичні величини, що характеризують рух твердого тіла: кутова швидкість і кутове прискорення.

Кутовою швидкістю тіла називають фізичну величину, що характеризує зміну кута повороту тіла в часі.

На підставі попередніх міркувань

[рад/с] . (2.42)

Якщо , то тіло в даний момент обертається в додатному напрямі.

Кутовим прискоренням називають фізичну величину, що визначає зміну кутової швидкості в часі.

Кутове прискорення можна знайти, якщо продиференціювати за часом кутову швидкість:

[рад/с²] . (2.43)

Якщо і одного знаку, то кутова швидкість зростає (обертання прискорене).

Наведені формули визначають і як скалярні величини. Далі розглянемо узагальнення означень кутових швидкості і прискорення.

Зауважимо, що і характеризують рух усього тіла.

Лінійними далі будемо називати швидкості і прискорення точок тіла на відміну від кутових і .

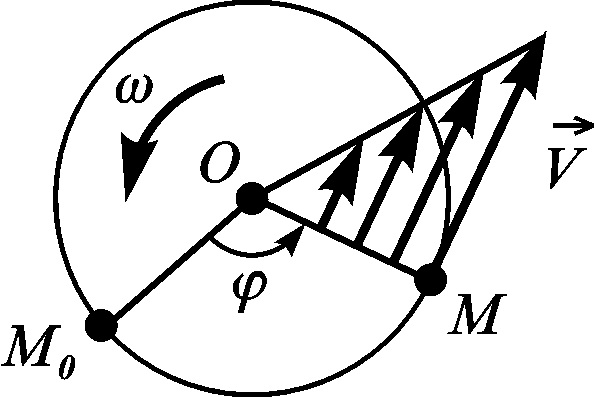
Розглянемо розподіл лінійних швидкостей у тілі, що обертається навколо нерухомої осі. Скористаємося натуральним способом визначення руху точки і розглянемо рух довільної точки тіла. Якщо початкове положення точки відповідає початковому значенню кута повороту , то з рис. 2.14 маємо:

,

де – відстань точки до нерухомої осі є радіусом обертання. Це рівняння є законом руху точки по траєкторії. Щоб знайти проекцію швидкості точки на дотичну до траєкторії, продиференціюємо за часом:

,

або

. (2.44)

Напрям вектора швидкості перпендикулярний до радіуса обертання .

Отже, лінійні швидкості залежно від радіуса обертання розподіляються за лінійним законом (рис. 2.15).

Щоб знайти розподіл лінійних прискорень, скористаємось формулами (2.34) і (2.44). Дістанемо

; ; (2.45)

; . (2.46)

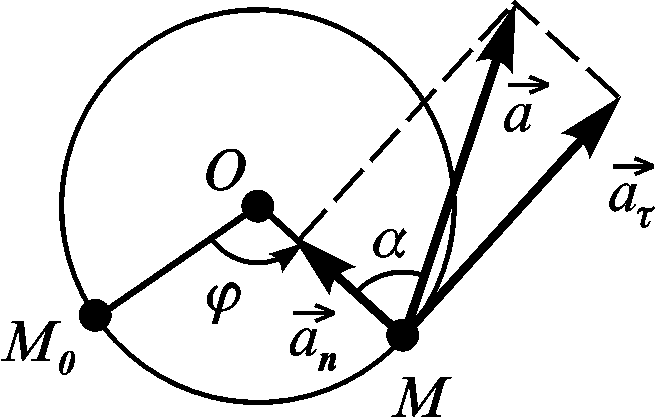
Модуль повного прискорення знайдемо за формулою

; . (2.47)

Кут між вектором повного прискорення і радіусом обертання (рис. 2.16):

. (2.48)

Рисунок 2.15	Рисунок 2.16

Оскільки і не залежать від положення точки на тілі, то кут однаковий для всіх точок тіла в певний момент часу.

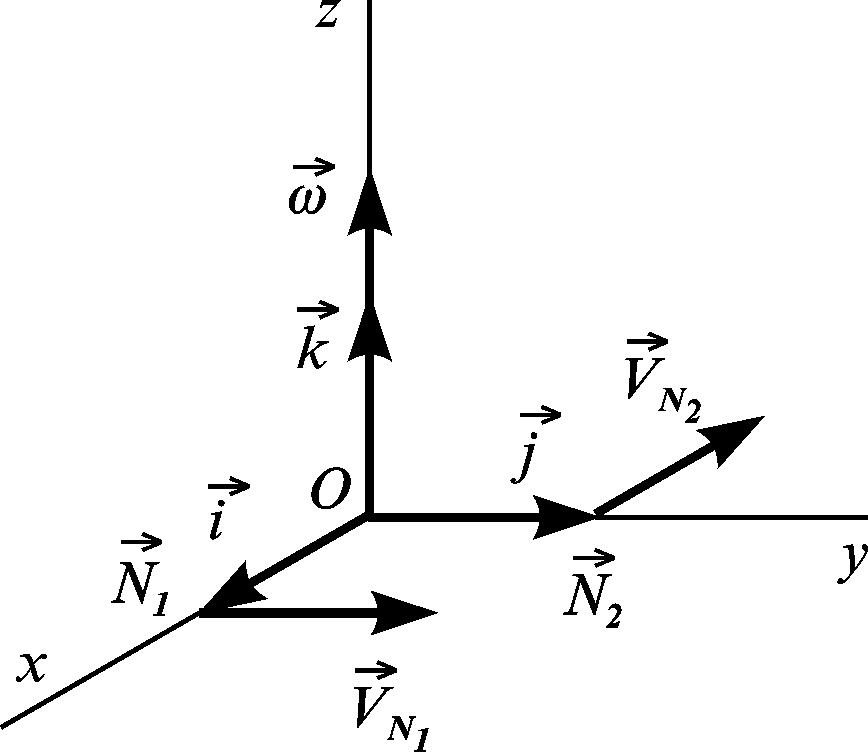
2.2.4. Вектори кутової швидкості і кутового прискорення. Формула Ейлера

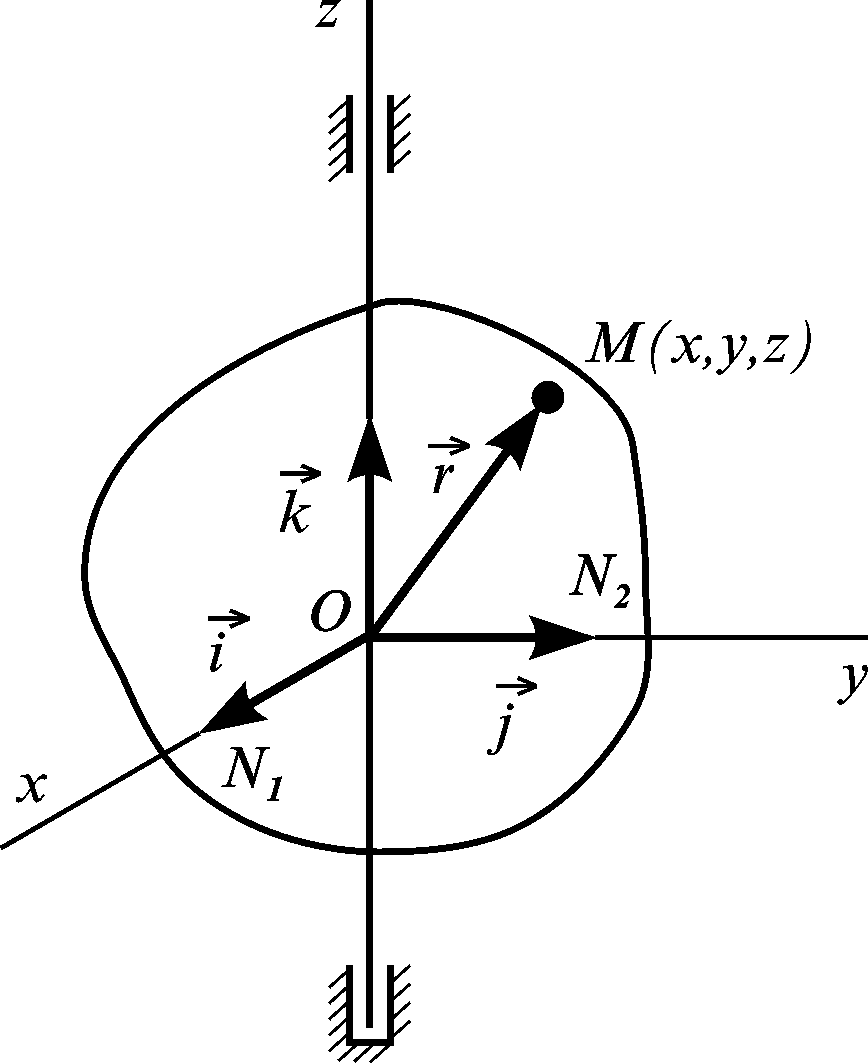
Узагальнимо поняття про кутову швидкість тіла, що обертається навколо осі. Виберемо початок прямокутної декартової системи координат на осі обертання (рис. 2.17) і вважатимемо, що вона незмінно зв’язана з тілом і обертається разом з ним. Орт лежить на нерухомій осі , орти і , зберігаючи модуль, змінюють напрям.

Визначимо швидкість довільної точки тіла. на підставі (2.15). Радіус-вектор розкладемо по ортах системи координат:

.

Рисунок 2.17	Рисунок 2.18