1.4. Розрахунково-графічна робота із застосуванням комп’ютера

“Розрахунок плоскої ферми”

Фермою називають геометрично незмінну систему прямолінійних стержнів, з’єднаних між собою шарнірами. Розглянемо тільки статично визначені ферми, для яких повинно виконуватись співвідношення , де – кількість стержнів, – кількість вузлів (шарнірів). Статично невизначені ферми розраховують методами будівельної механіки.

При розрахунках ферм стержні вважатимемо невагомими. Активні сили прикладатимемо до ферми лише у вузлах (шарнірах). Розрахунок ферми полягає у визначенні реакцій опор ферми і зусиль, що виникають в її стержнях під дією зовнішніх сил. Відомими вважають конфігурацію ферми та її лінійні розміри.

З усіх методів розрахунку ферм найчастіше застосовують метод Ріттера (аналітичний) та метод вирізання вузлів (аналітичний та графічний – діаграма Максвелла-Кремони). Якщо ферма має складну геометрію, то доцільніше використовувати графічні методи та комп’ютерні розрахунки з метою виключення помилок.

Приклад виконання розрахунково-графічної роботи

“Розрахунок плоскої ферми”

Завдання на розрахунково-графічнУ роботУ

Умова. Для заданої ферми

1. за допомогою комп’ютера:

• спроектувати:

— задану схему ферми,

• ферму, звільнену від в’язей;

• ферму із заданими навантаженнями та розрахованими реакціями в’язей;

• розрахувати:

• реакції в’язей та зусилля у стержнях;

2) за допомогою графічних методів

• визначити зовнішні реакції (вірьовочний багатокутник Варіньйона);

• визначити зусилля у стержнях ферми (діаграма Максвелла-Кремони).

Завдання: Плоска ферма (рис. 1.39) знаходиться в рівновазі під дією зовнішніх сил: = 58 кН; = 50 кН; = 85 кН [ 16 ].

Рисунок  1.39

Виконання

1. Для заданої ферми (рис. 1.40) за допомогою комп’ю-тера:

• спроектувати:

— задану схему ферми,

• ферму, звільнену від в’язей;

• ферму із заданими навантаженнями та розрахованими реакціями в’язей.

• розрахувати:

— реакції в’язей та зусилля у стержнях;

Для зручності програмування пронумеруємо (рис. 1.40) вузли (табл. 1.1), кінці векторів реакцій в’язей (табл. 1.2), стержні (табл. 1.3) та вектори реакцій в’язей (табл. 1.4) наступним чином.

Рисунок 1.40

Таблиця 1.1

Номер вузла	1	2	3	4	5	6
Позначення	А	С	D	E	Q	L
Сила, прикладена у вузлі	,			–	–
Номер вузла	7	8	9	10	11	12
Позначення	V
Сила, прикладена у вузлі	–	–	–	–	–

Таблиця 1.2

Номер вузла	0	13	14	15
Позначення
Сила, прикладена у вузлі		–	–	–

Таблиця 1.3

Номер стержня	1	2	3	4	5	6	7
Позначення	АС	АК	CD	CK	CW	DE	DW
Номер стержня	8	9	10	11	12	13	14
Позначення	DU	EQ	EU	QL	QU	QG	LV
Номер стержня	15	16	17	18	19	20	21
Позначення	LG	LH	VH	KW	WU	UG	GH

Таблиця 1.4

Номер стержня	22	23	24
Позначення

Далі складаємо програму в середовищі Maple [8], за допомогою якої змоделюємо задану схему ферми; ферму, звільнену від в’язей та ферму з розрахованими навантаженнями. У табл. 1.5 наведено текст програми “Розрахунок плоскої ферми”, який розбито на блоки з метою детального пояснення змісту елементів математичного моделювання.

2) за допомогою графічних методів

• визначити зовнішні реакції (вірьовочний багатокутник Варіньйона);

• визначити зусилля у стержнях ферми (діаграма Максвелла-Кремони).

• Метод Варіньйона¹

Розглянемо систему, що складається з декількох сил на площині [6]. Ми покажемо метод, який дозволяє звести цю систему сил до збіжної системи двох сил або до пари сил. Цей метод належить Варіньйону. Розглянемо, як приклад, систему трьох сил , що лежать в одній площині (рис. 1.41, а). Спочатку припустимо, що векторна сума цих сил

Далі дослідимо й інші випадки.

Щоб звести цю систему сил до системи двох збіжних сил, використаємо побудову, що належить Варіньйону.

Виберемо масштаб для сил і побудуємо у цьому масштабі багатокутник сил (рис. 1.41, б), на якому позначено:

; ; ; .

Виберемо на площині довільну точку О (полюс) і проведемо з неї у вершини багатокутника сил промені , , , . Розкладемо кожну силу по двох напрямах, які збігаються з променями, проведеними в початок й у кінець вектора сили. Так, силу розкладемо на складові та , силу — на складові і , силу — на складові та . Тепер розкладемо ці сили там, де вони фізично прикладені (рис. 1,41, а). Виберемо довільно точку А на лінії дії сили як точку її прикладання і проведемо через

цю точку промені, паралельні променям і . На цих прямих лежатимуть складові вектора сили . Оскільки на промені лежить одна із складових сили , продовжуємо пряму, паралельну променю , до її перетину з лінією дії сили у точці В – точки її прикладення. Через точку В проводимо пряму, паралельну променеві , до її перетину з лінією дії сили у точці С. Знову вважатимемо точку С точкою прикладання сили . У результаті одержуємо ламану лінію з вершинами на лініях дії сил . Цю ламану лінію називають багатокутником Варіньйона.

а б

Рисунок 1.41

Перенесемо складові сил , одержані в результаті їх розкладу по напрямах променів, на сторони багатокутника Варіньйона. Складові, які спрямовані вздовж внутрішніх сторін багатокутника Варіньйона, зрівноважуються. Отже, залишається система двох збіжних сил, які діють вздовж крайніх сторін багатокутника Варіньйона, паралельних променям і . Вони перетинаються у точці – прикладання рівнодійної сил . Щоб знай-ти вектор рівнодійної, треба перенести сили і в точку і додати за правилом паралелограма. Однак додавання цих сил найзручніше зробити на багатокутнику сил

.

Побудова багатокутника Варіньйона поширюється на довільну кількість сил на площині. Отже, можна стверджувати, що рівнодійна довільної системи сил на площині, якщо вона існує, дорівнює векторній сумі сил системи:

.

Точка її прикладання лежить у точці перетину крайніх сторін багатокутника Варіньйона, а лінія дії, що проходить через цю точку, паралельна вектору, що з’єднує початок вектора і кінець вектора .

Багатокутник Варіньйона називають вірьовочним або мотузковим багатокутником. Ця назва походить від того, що формою рівноваги гнучкої нерозтяжної нитки, закріпленої у крайніх точках багатокутника Варіньйона і навантаженої у точках відповідно силами , є багатокутник Варіньйона. Кожна його вершина лежить на лінії дії певної сили.

Нарешті, розглянемо деякі взаємні властивості багатокутників сил і Варіньйона. Проаналізуємо різні випадки, які можуть трапитись при перетворенні системи сил на площині за допомогою метода Варіньйона.

• Багатокутники сил і Варіньйона незамкнені. Цей випадок вже розглянутий. При умові незамкненості обох багатокутників система сил зводиться до рівнодійної.

• Багатокутник сил замкнений, а багатокутник Варіньйона незамкнений. У цьому випадку система сил зводиться до пари сил.

• Багатокутник сил незамкнений, а багатокутник Варіньйона замкнений. Цей випадок не належить до істотно відмінних від попередніх і зводиться до першого випадку.

• Багатокутники сил і Варіньйона замкнені. У цьому випадку система сил на площині зрівноважена.

Отже, приходимо до висновку, що плоска система сил може зводитись до рівнодійної або пари сил, а також зрівноважуватись.

Таким чином, довільна система сил на площині зрівноважується тоді і лише тоді, коли виконуються умови замкнутості багатокутників сил і Варіньйона.

Розглянемо тепер приклад застосування графічної умови рівноваги до визначення опорних реакцій плоскої ферми (рис. 1.39).

Зазначимо, що у випадку застосування графічних методів насамперед потрібно вибрати зручні масштаби сил і довжин, графічно зобразити ферму з прикладеними до її вузлів відомими силами та позначити вузли. Далі перевірити, чи є дана ферма статично визначеною. Кількість вузлів цієї ферми ; тоді кількість стержнів повинна дорівнювати, , що відповідає даній фермі (див. рис. 1.40).

• До ферми прикладені три активні сили: , , , реакції стержня та нерухомого шарніра (рис. 1.40). Реакція стержня прикладена до ферми у точці L і спрямована вздовж лінії, що проходить через точкові шарніри L та B, а реакція – у точці A, і її напрям невідомий. Відомі сили , , необхідно розташувати з одного боку від прямої , що з’єднує точки прикладання невідомих сил , . Тому сили і переносимо вздовж лінії їхньої дії у вузли і 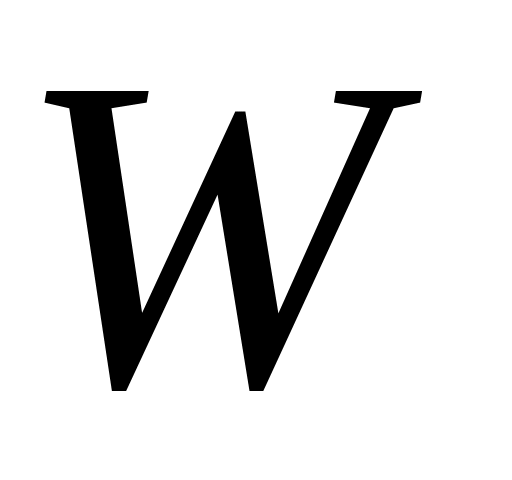(рис. 1.42, а). Це не позначиться на визначенні опорних реакцій ферми як твердого тіла.

• Оскільки ферма перебуває у стані рівноваги, по-будуємо замкнені силовий (рис. 1.42, б) та вірьовочний (рис. 1.42, а) багатокутники. Зазначимо, що для побудови силового багатокутника треба ферму обходити в одному напрямі, починаючи від точки – прикладання реакції неідеальної в’язі (на рис. 1.42, а – за ходом годинникової стрілки), так як побудову починаємо з відомих сил.

• Побудову починаємо із силового багатокутника. На рис. 1.42, б відкладаємо вектор , до нього додаємо вектори і , з точки 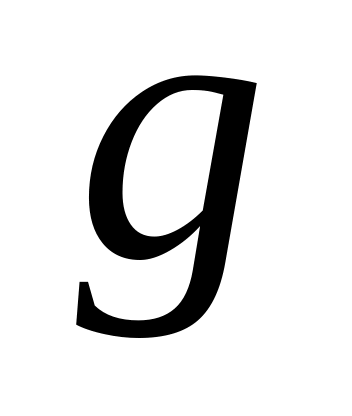проводимо пряму , паралельну вектору .

Вірьовочний багатокутник ВАРІНЬЙОНА

а

а

Силовий багатокутник

б

Рисунок 1.42

• Далі на рис. 1.42, б вибираємо довільну точку O і з’єднуємо її з попередньо побудованими точками .

• Оскільки лінія дії реакції невідома, а відома лише точка А її прикладання, то побудову вірьовочного багатокутника (рис. 1.42, а) необхідно починати не з довільної точки, а саме з точки А. З неї проводимо лінію, паралельну променю до перетину з лінією дії сили в точці b. З точки b проводимо лінію, паралельну променю до перетину з лінією дії сили у точці е. З точки е проводимо лінію, паралельну променю до перетину з лінією дії сили у точці f. З точки f проводимо лінію, паралельну променю до перетину з лінією дії сили у точці g. З’єднавши точки g і A, замикаємо вірьовочний багатокутник.

• Далі з точки O на рис. 1.42, б проводимо промінь , паралельний стороні Ag вірьовочного багатокутника (рис. 1.42, а), до перетину з прямою і отримуємо точку а. З’єднавши і , отримуємо замкнений силовий багатокутник . Зусилля у стержні : , а реакція нерухомого шарніра .

Вимірюємо знайдені реакції в’язей, враховуючи вибраний масштаб, і порівнюємо з результатами, розрахованими на комп’ютері.

Діаграма Максвелла-Кремони

З побудови багатокутника Варіньйона видно, що кожній вершині багатокутника сил відповідає певний промінь, тобто сторона багатокутника Варіньйона. І навпаки, кожній вершині багатокутника Варіньйона відповідає певна сила, для якої ця вершина є точкою прикладання сили. Ці взаємні властивості дозволяють запровадити так зване подвійне позначення сил. А саме, вектор кожної сили можна вважати напрямленим відрізком, який з’єднує дві послідовні вершини багатокутника сил.

• Зобразимо ферму в лінійному масштабі і введемо позначення сил за допомогою полів (рис. 1.43, а):

• поля, за допомогою яких позначаються зовнішні сили, є частинами площини, що обмежені зовнішніми контурами ферми та лініями дії двох суміжних зовнішніх сил. Обходимо ферму, наприклад, проти ходу годинникової стрілки і позначаємо поля  – ;

• поля, за допомогою яких позначаються внутрішні сили (зусилля в стержнях), є окремими трикутниками всередині ферми. Позначаємо поля  – 15.

Основою для діаграми Максвелла-Кремони є багатокутник зовнішніх сил, до якого добудовують багатокутники внутрішніх сил. Тому, насамперед, необхідно побудувати замкнений багатокутник зовнішніх сил , а далі, застосувавши метод вирізання вузлів, визначити внутрішні сили – зусилля у стержнях ферми. Отже, будуємо замкнутий силовий багатокутник зовнішніх сил за вже відомими опорними реакціями в’язей (рис. 1.43, б) у вибраному масштабі:

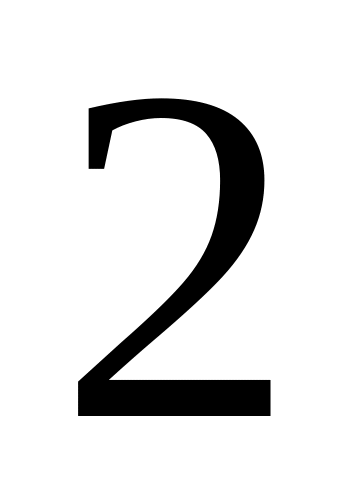• з точки відкладаємо вниз вектор і отримуємо точку , з точки відкладаємо вектор вниз і отримуємо точку , з точки відкладаємо вектор вгору і отримуємо точку , з точки відкладаємо вектор і отримуємо точку , яку з’єднуємо з точкою . В результаті повинні отримати останню зовнішню силу . Таким чином, діаграма зовнішніх сил (заданих та реакцій в’язей) побудована (рис. 1.43, б).

• Продовжуємо побудову діаграми Максвелла-Кремони.

Зазначимо, що кожному вузлу ферми відповідає замкнений силовий багатокутник, оскільки кожний вузол ферми перебуває у стані рівноваги.

Зауваження. При побудові діаграми може трапитися, що деякі точки збігаються (див. рис. 1.43, б, точки і ). Це означає, що стержні EU, HV і LV, які відповідають цим позначенням (рис. 1.42, д) не навантажені(нульові). Такі стержні встановлюють у фермі лише з конструктивних міркувань. Відзначимо також, що нульові стержні можна визначити без побудови діаграми. Такі стержні трапляються у наступних випадках: