Формула Ньютона-Лейбница

Определенный интеграл вычисляется по формуле , которая называется формулой Ньютона-Лейбница, где F(x)  первообразная функция для f(х), т.е. F(x) = f(x), F(х)  непрерывная на [а, в] и дифференцируемая на интервале (а, в).

Обозначим символически .

Тогда формулу Ньютона-Лейбница можно записать так:

.

Пример. .

Свойства определенных интегралов

Свойство 1

, где k  постоянная величина

Свойство 2

Если функции f(x), (х) интегрируемы на [а, в], то .

Свойство 3

, где а  с  в

Свойство 4 .

Свойство 5

Если функция f(х) интегрируема на [а, в] и m  наименьшее значение f(х) на интервале [а, в], а М  наибольшее значение f(х) на [а, в], то имеет место соотношение

.

Свойство 6 ( теорема о среднем )

Если f (x) непрерывна на [а ,в],то существует точка  [а, в] такая, что

= (в - а) f().

Доказательство

По формуле Ньютона-Лейбница .

Функция F(х) непрерывна на [а, в] и дифференцируема на (а, в), следовательно, к ней можно применить теорему Лагранжа:

существует  (а, в) такая, что

F(в) - F(a) = (в - а)F() = (в - а)f(). Окончательно, = (в - а)f().

Методы вычисления определенного интеграла

Интегрирование по частям

.

Получим формулу .

Пример. Найти , .

Замена переменной (подстановка в определенном интеграле)

Предположим, что для вычисления интеграла удобно относительно оси координат. совершить подстановку х = (t), при этом функции f[(t)], (t), (t), непрерывны в интервале [t₀, t₁], t₀, t₁ находят из равенства (t₀) = а, (t₁)= в. Подстановка в определенном интеграле производится следующим образом: .

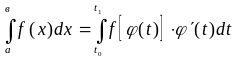Пример.

Замечание.

1. Интеграл можно вычислить при помощи подстановки х = а sint (или х = а cos t)

2. Интеграл можно вычислить при помощи подстановки х = а tg t

3. Интеграл можно вычислить при помощи подстановки x = a sect (или x = a cosec t)

Несобственные интегралы

Понятие определенного интеграла было введено при выполнении следующих условий:

если интервал [а, в] конечный, а функция f(х) непрерывна или монотонна или ограничена на этом интервале.

Если одно из условий нарушено, то вводится понятие несобственного интеграла.

Интегралы с бесконечными пределами

Это интегралы вида:

,

которые мы будем называть несобственными интегралами и они определяются равенствами:

, , .

с  произвольная точка числовой оси.

Если пределы, стоящие справа, существуют и имеют конечный предел, то говорят, что несобственный интеграл существует или сходится.

В противном случае говорят, что несобственный интеграл не существует или расходится.

Пример. Вычислить .

,

следовательно, несобственный интеграл сходится.

Несобственный интеграл от функции с бесконечным разрывом

Пусть функция f(х) , заданная на интервале [ a, в], имеет бесконечный разрыв в точке х = а, а в остальных точках интервала непрерывна.

Несобственным интегралом функции f(х) на [ a, в] называют предел (если он существует) .

Говорят, что в случае существования конечного предела несобственный интеграл сходится, если не существует или равен бесконечности, то расходится.

Пусть f(х) имеет точку разрыва х = в, тогда понятие несобственного интеграла вводится аналогично предыдущему:

Пусть f(х) имеет точку разрыва х = с, где а  с  в , тогда под несобственным интегралом от f(х) на [ a, в] , если оба предела существуют, и по определению

.

Если оба предела имеют конечный предел, то говорят, что несобственный интеграл сходится, в противном случае - расходится.

Пример. Вычислить .

х = 1 - точка разрыва функции, и, тогда

,

следовательно, несобственный интеграл сходится.