Лабораторная работа №4 Гетерогенное химическое равновесие
Цель
Определение константы равновесия и расчет основных термодинамических величин реакции разложения оксида никеля
Приборы и реактивы
1. Измерительная система (печь, ячейка из ZrO2 с 10 % Y2O3, термопара)
2. Универсальный регулятор Zirconia 318
3. Порошковая смесь NiO\Ni
Схема установки
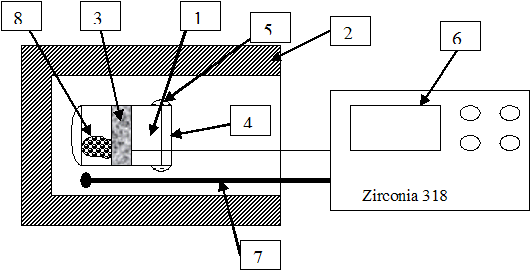
Схема установки для измерения давления диссоциации оксидов металлов методом ЭДС: реакционный сосуд (1), выполненный из оксида циркония с добавкой 10% оксида иттрия; электропечь (2); пористые платиновые электроды (3); алундовая крышка (4); герметизирующее высокотемпературное стекло (5). Температура в печи поддерживается при помощи регулятора Zirconia 318 (6) и термопары (7).
Порядок выполнения работы
Включают печь и с помощь регулятора Zirconia 318 устанавливают первоначальную температуру реакционного сосуда 600 °С, запускают на компьютере программу "Регистрация" для получения данных с регулятора. После установления постоянной температуры дожидаются установления равновесного парциального давления кислорода над системой оксид\металл. После этого с помощью регулятора повышают температуру в печи на 20 градусов и снова дожидаются установления постоянного давления.
Таким образом, поэтапно повышая температуру, проводят около 10 замеров. Измерения проводят до тех пор, пока температура не достигнет 800 °С. После этого сохраняют полученные на компьютере данные в файл. Горизонтальные участки на графике [log(pO2)-время] соответствуют значениям равновесных парциальных давлений кислорода над системой Ni/NiO.
Обработка результатов
Таблица экспериментальных данных
При разложении оксида кобальта протекает реакция (1)
NiO=Ni + ½ O2, Kp=pO21/2 (1)
Соответствующие измеренные значения температуры T °C и давления диссоциации lg(pO2/атм) вводятся вручную в колонки с именами T,C и lg(PO2), в остальные колонки значения добавляются в результате выполнения программного кода, помещенного между метками "Начало заполнения таблицы" и "Конец заполнения таблицы".
> restart;
> with(Spread);
> ssid:=CreateSpreadsheet(Table);
|
A |
B |
C |
D |
E |
F |
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
9 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
11 |
|
|
|
|
|
|
> #Начало заполнения таблицы#
> N:=11;
> for i from 2 to N do
for j from 2 to 2 do
SetCellFormula(ssid,i,j,GetCellValue(ssid,A||i)+273.15)
end do:
end do:
> for i from 2 to N do
for j from 3 to 3 do
SetCellFormula(ssid,i,j,1/GetCellValue(ssid,B||i))
end do:
end do:
> for i from 2 to N do
for j from 5 to 5 do
SetCellFormula(ssid,i,j,GetCellValue(ssid,D||i)*0.5)
end do:
end do:
> for i from 2 to N do
for j from 6 to 6 do
SetCellFormula(ssid,i,j,GetCellValue(ssid,E||i)*GetCellValue(ssid,B||i))
end do:
end do:
> #Конец заполнения таблицы#
Описание математических преобразований
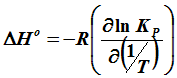
Следовательно, чтобы найти стандартные энтальпию и энтропию реакции, необходимо найти тангенсы угла наклона графиков прямых в соответствующих координатах [lg(Kp)-(1/T)] и [T*lg(Kp)-T]
Математические преобразования
> restart;
> data1:=zip((x,y)->[x,y], [seq(Spread[GetCellValue](Table, i, 3), i=2..11)], [seq(Spread[GetCellValue](Table, i, 5), i=2..11)] ):
> line1:=CurveFitting[LeastSquares](data1, x);
> with(plots):
Pdot1:=pointplot(data1, symbol=circle, color=blue,symbolsize=15, labels=["1/(T,K)", "log(Kp)"], labeldirections=[horizontal, vertical], legend="Эксперимент"):
Pline1:=plot(line1, x=data1[nops(data1),1]..data1[1,1], legend="МНК"):
display(Pdot1, Pline1, caption="Зависимость константы равновесия\n реакции (1) от обратной температуры\n lgKp - 1/T",axes=boxed);
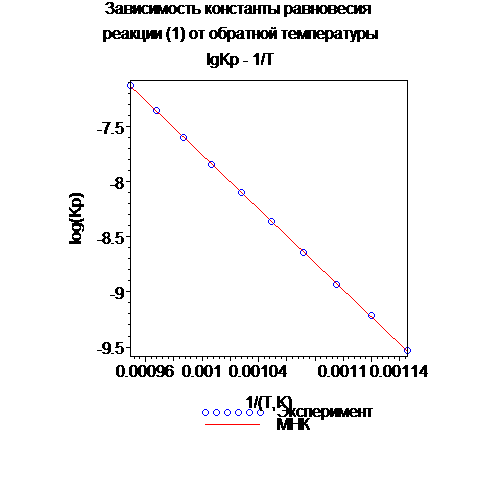
> data2:=zip((x,y)->[x,y], [seq(Spread[GetCellValue](Table, i, 2), i=2..11)], [seq(Spread[GetCellValue](Table, i, 6), i=2..11)] ):
> line2:=CurveFitting[LeastSquares](data2, x);
> Pdot2:=pointplot(data2, symbol=circle, color=blue,symbolsize=15, labels=["T, K", "T*log(Kp)"], labeldirections=[horizontal, vertical], legend="Эксперимент"):
Pline2:=plot(line2, x=data2[nops(data2),1]..data2[1,1], legend="МНК"):
display(Pdot2, Pline2, caption="Зависимость T*log(Kp) от температуры T\n для реакции (1)",axes=boxed);
> Delta*H=-2.3025*coeff(line1, x)*evalf(ScientificConstants[Constant](R));
Ошибка,процент(Delta*H)=abs((rhs(%)-234750)/234750)*100;
Delta*S=2.3025*coeff(line2, x)*evalf(ScientificConstants[Constant](R));
Ошибка,процент(Delta*S)=abs((rhs(%)-85.6)/85.6)*100;
>
Выводы
В ходе работы мы определили константы равновесия (см. таблицу) и провели расчет стандартных изменения энтальпии (234859.91 Дж) и энтропии (86.78 Дж/К) реакции разложения оксида никеля. Погрешности вычисленных термодинамических величин оказались довольно небольшими (0.05% и 1.38%), что определяется высокой точностью определения равновесного давления диссоциации оксида методом ЭДС.