2.8. Лінійний регресійний аналіз

Зміна результативного ознаки може бути обумовлено загальним впливом декількох факторних признаків. У цьому випадку взаємозв'язок між ознаками для генеральної сукупності задається функцією регресії

М (У / Х₁ = х₁} ..., X_m = х_m) = а₀+a₁x+ … + а_mх_m.

Завданням регресійного аналізу є оцінка параметрів функції регресії а₀, а₁,…. а_m за вибірковими даними.

Визначимо рівняння регресії по функції регресії, замінивши параметри а_i, - їх оцінками:

( x₁,х₂, ... , x_m) = а₀ + а₁x₁ + а₂х₂ + … + а_mx_m (2.36)

Дане рівняння відображає лінійну залежність результативної ознаки від декількох факторних; моделі такого виду отримали назву багатовимірних лінійнихних регресійних моделей. Коефіцієнт а_і {показує, на скільки одиниць зміниться результативна ознака у, якщо факторний х_і зміниться на одну одиницю, а решта залишаться колишніми.

Припустимо, проведена вибірка об'єму n, результати якої можна представити матрицею X і вектором У

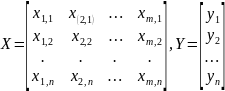
Для оцінки параметрів регресії використовуємо метод найменших квадратів, згідно з яким сума квадратів відхилень вибіркових значень результативної ознаки від обчислених по рівнянню регресії має бути мінімальною. У відповідності з принципом найменших квадратів маємо

Функція F приймає мінімум при таких значеннях шуканих параметрів а₀, а₁,…. а_m, при яких її виробництво по цих параметрах дорівнюють нулю

Визначаючи приватні похідні від функції F, приходимо до наступної системи рівнянь:

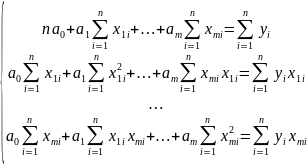(2.37)

Для обчислення коефіцієнтів а₀, а₁,…. а_m систему рівнянь (2.37) можко вирішити будь-яким відомим в лінійної алгебри методом. Розглянемо, наприклад, метод оборотної матриці, найбільш часто використовуваний для статистичних розрахунків у зв'язку з застосуванням ЕОМ.

З першого рівняння системи (2.37) отримаємо

Підставивши в інші рівняння системи замість а₀ отримані вираз і враховуючи, що 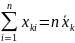приходимо до наступної системи рівнянь:

Розглянемо алгоритм формування коефіцієнтів при невідомих а₀, а₁,…. а_m і вільних членів системи рівнянь (2.38). Позначимо: W- Матриця коефіцієнтів при невідомих розміру m×m V - вектор-стовпець вільних членів розміру m×1. Введемо в розгляд матрицю 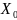і вектор елементи яких центровані відносно своїх середніх значень:

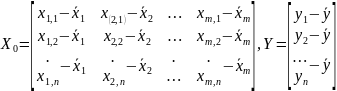
Покажемо, що W= , і вектор V=  , де – транспонована матриця . Дійсно:

[Покажемо, що № = Х'0Х0, V = ХоУ0, де Х'0 - транспо ¬ лося раніше матриця Х0. Дійсно,

1 п п

= £ (хм - хк) (хі - * /) = £ - • *: * £ -

1 = 1 1 = 1

п п п

- XI £ Хи + £ Хкх1 = £ ХмХі-ПХкХ1 \

* = 1 1 = 1 п = 1

п __ п __ л

= £ (* «- **) - У) = £ хнУ1 - £ У1 -

1 = 1 1 = 1 4 = 1

п п п

- У £ + £ пекло = £ - Л ГКУ. 1 = 1 1 = 1 1 = 1

Систему рівнянь (2.38) запишемо у матричному вигляді К / А = V, де Л '= (ав а2, ..., ап).

Нехай - матриця, зворотна матриці. Шуканий вектор А знаходимо з виразу А = V, звідки визна ¬ ділячи та розрахункові формули для параметрів

т

4 = 1, 2 / я, (2.39)

т _

«Про = - £« Л-(2.40)

Таким чином, алгоритм розрахунку параметрів рівняння регресії за даними матриці X і вектору У зводиться до сле-; дующим діям:

? 1. Обчислення середніх значень факторних і резуль-

п

татівного ознак хк = У] х ^ / п, 6 = 1, 2, ..., т \ у -

п

■ «= £ у> / п. 1

2. Формування матриці Х0 і вектора елементи ^ яких центровані щодо своїх середніх зна-[чений.

3. Визначення матриці коефіцієнтів при невідомим \ вих V? = ХоХ0 і вектора вільних членів V = Х0К0. 4. Обчислення матриці й? -1, Зворотної матриці Ж.

5. Розрахунок шуканих параметрів рівняння регресії по формулах (2.39), (2.40).

Оцінкою залишкової дисперсії СГОСТУ є вибороч ¬ ва залишкова дисперсія 5ост, яку можна визначити за формулою

п

5ост = £ (У (- У (хі, х2 {ХТ1)) 21К, (2.41)

1 = 1

де К - число ступенів свободи (К = ■ п - т - 1).

Рівняння регресії у (х'х2, ..., хт) є точеч ¬ ної оцінкою умовного математичного очікування

М (У/Х1 = х19 Х2 - х2, ..., хт »хт).

Очевидно, що ця оцінка може змінюватися при пере ¬ ході від однієї вибірки до іншої. Тому для умовного ма ¬ тематичного очікування визначимо довірчий ін ¬ інтервал.

Дисперсія умовного середнього у (X) в точці Х ° = ж

/ 00 • 0ч

«= (Хі х2, ХТ) дорівнює

= 5ост [4 - + - *> - ху] • (2-42)

Довірчий інтервал може бути знайдений з умови

\ | К * °> /

де а - рівень значимості; - критичне значення статистики Стьюдента при К ступенях свободи і рівні значущості а (див. табл. 2.13). Отже, умовне ма ¬ тематичне очікування М (У1Х = Х °) з імовірністю 1 - а потрапляє в інтервал

у (Х °) - <М {УIX = Х °) <у (Х °) + 5 - (Х0)

(2.43)

Аналогічно можна встановити довірчий інтервал для кожного параметра функції регресії а0, А19 ..., ат, оскільки коефіцієнти регресії розраховуються за вибірковими даними і при зміні обсягу вибірки або при переході від однієї вибірки до іншої можуть змінюватися.

Дисперсії коефіцієнтів регресії визначають за формулами

«Я = 5осТ Н-+ Х1Г1Х '; (2.44)

Яа, = 5ост ^ \ к = 1, 2, ... , Т, (2.45)

де X - (х'Х2у хт). 56 /

Довірчі інтервали для ак при числі ступенів

свободи до і рівні значущості а визначаються неравен-ством

ак - Еа ^ К.А <а * <ак + 8а ^ до, а-(2.46)

Відзначимо, що довірчий інтервал для параметра ак може захопити область як позитивних, так і від ¬ ріцательних значень (що можливо, якщо | ак | ^ ^ У такому випадку коефіцієнт регресії ак і оце ¬

Нива їм параметр ак можуть мати різні знаки. Це протиріччя можна пояснити тим, що в дійсності параметр ак = 0 (результативна ознака не залежить від факторного ознаки хк), а відмінність коефіцієнта регрес ¬ ці ак від нуля (в ту чи іншу сторону) обумовлено огра ¬ ничен обсягом вибірки і впливом неврахованих слу ¬ чайних факторів. Тому перевіряється значимість оцінок параметрів регресії: для кожного коефіцієнта регрес ¬ ці ак обчислюють статистику = ^ ^, & = О, 1, 2, ...

ч

..., Т, і порівнюють її з критичним значенням ^, Апрі за ¬ даних рівні значущості а і числі ступенів свободи К. Якщо 4> 1к, а> то припущення про рівність нулю коефі ¬ цієнта регресії ак відкидається і його вважають значимим. Якщо ж <tкta, то немає підстав відкидати дане пред ¬ положення та оцінку ак вважають незначущою.

Крім оцінки значущості кожного коефіцієнта рег ¬ рессіі оцінюють також значимість рівняння регресії. У зв'язку з цим висловлюється гіпотеза, що всі коеффіціен ¬ ти регресії, крім а0, дорівнюють нулю (ця гіпотеза називаючи ¬ ється нульовою і позначається Н0). Перевірка гіпотези Н0 здійснюється за допомогою статистики Фішера

(О-Зост) / *! (24л

де, (2ОСт - сума квадратів відхилень результативної ознаки відповідно від середнього значення і від умовно ¬ го середнього у (х'х2, ..., хт) \ К \ = т \ К2 = п - т - I. При заданому рівні значимості а для ступенів свободи К \ і К2 по таблиці ^-розподілу Фішера знаходять крі ¬ тичні значення Р (К19 К2, а) і порівнюють його з розрахунок ¬ вим, визначеним за формулою (2.47). Якщо Т7> Б (/ Сх, К2, а), то гіпотезу / / 0 про одночасне рівність нулю всіх коефіцієнтів регресії відкидають і рівняння рег-рессіі вважають значимим. Якщо ж Т7 <^ (Кь ^ Са »а)> то

* 1

/ С, • 2 3 4 5 6 7 8 9 10

   

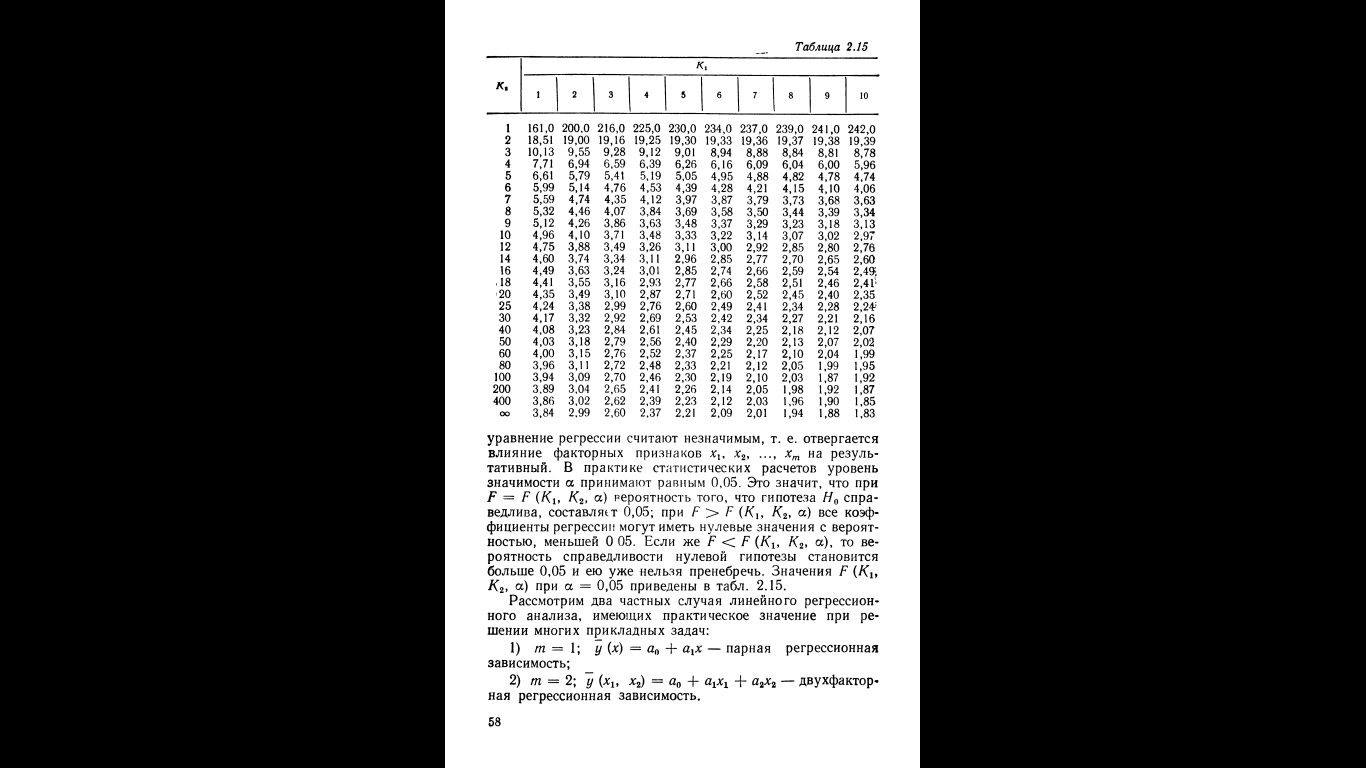
рівняння регресії вважають незначущим, тобто відкидається вплив факторних ознак хХч л: 2 ..., хт на резуль ¬ татівний. У практиці статистичних розрахунків рівень значимості а приймають рівним 0,05. Це означає, що при Т7 = Т7 {Кь К2, ймовірність того, що гіпотеза Н0 спра ¬ ведливо, становить 0,05; при Р> ^ (Кх> / С2, а) всі коеф ¬ вантаження регресії можуть мати нульові значення з вероят ¬ ністю, меншою 0 05. Якщо ж Т7 <Т7 (/ Сь К2> а), то ве ¬ роятность справедливості нульової гіпотези стає більше 0,05 і нею вже не можна знехтувати. Значення Т7 (Кі К2, а) при а = 0,05 наведені в табл. 2.15.

Розглянемо два приватних випадку лінійного регресійного ¬ ного аналізу, що мають практичне значення при ре ¬ шеніі багатьох прикладних задач:

1) т = 1; у (х) = а0 + ахх - парна регресійна залежність;

2) т = 2; біля (хі х2) = а0 + Аххх + а2х2 - двухфактор * ная регресійна залежність.

Парна регресійна залежність. Для випадку т = 1 система рівнянь (2.38) записується так:

а1 ^ £ - = £ У1Х1 - пух • Матриця № і вектор К мають розмірність 1 X 1 і рав-

п __ л

Ни відповідно № = £ - ПХ2, У = £ В (Х1 - 1 = 1 £ = 1

- Пух; зворотна матриця визначається формулою

Ц7 "1 = 1 / (2 \ * = 1

звідки слідують розрахункові формули для параметрів уравне ¬ ня регресії аг і а0:

п

£ У 1 * 1 - пух

ах ==, (2.48)

£

= ^ - (2.49)

Дисперсія умовного середнього у (. Х) в точці х = А; 0 рас ¬

зчитується за формулою _ с2

у {Х) - ^ о

. (2.50)

Пха

1, (х0-х) * п п

V А-

1 = 1

Виходячи з формул (2.44) і (2.45), отримаємо дисперсії коефіцієнтів парної регресії

51 = 5ост (~ + • (2.51)

V 1

5а, = 5 ^ ст / (| 1 х] - л * 2). (2.52)

Приклад. Установім'регрессіонную залежність собівартості 1 т вугілля у від потужності пласта корисної копалини х по середньомісячним даним, представленим у статистичній звітності шахти.

Вихідні дані і проміжні розрахунки наведені в табл. 2.16,

Використовуючи дані таблиці, отримаємо

х = 2 ^ / 12 = 1,66; у = 2 ^ / 12 = 15,4;

ІГ

в

2 X

до * а

ЕГ см * до * нҐ и 'I 3

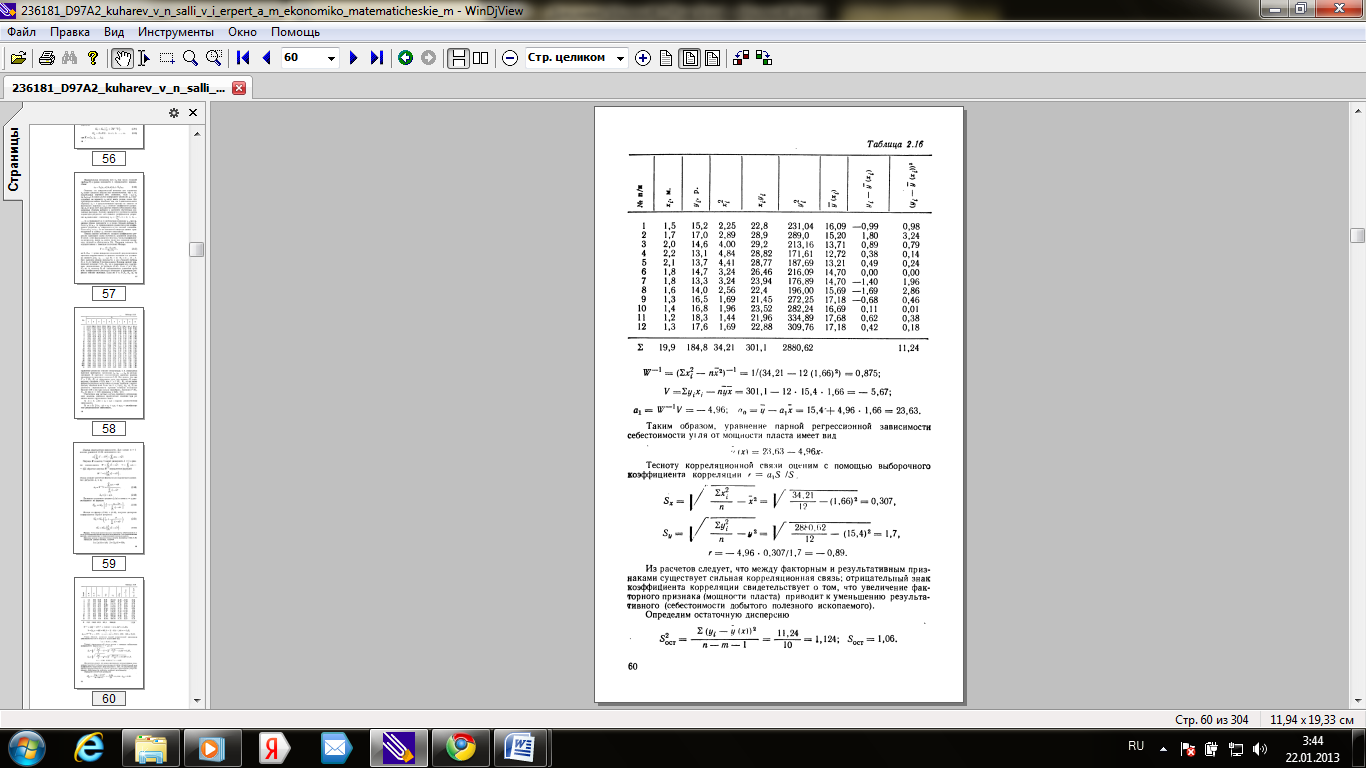
ІГ "1 = (1х з - пх2) -1 = 1 / (34,21 - 12 (1,66) 2) = 0,875; V = 301,1 - 12. 15,4. 1,66 = - 5, 67;

а1 === - 4,96; - 15,4 + 4,96. 1,66 = 23,63.

Таким чином, рівняння парної регресійної залежності собівартості вугілля від потужності пласта має вигляд

• їх) = 23,63 - 4,96 *.

34,21 12

Тісноту кореляційної свя: 1і оцінимо за допомогою вибіркового коефіцієнта кореляції г - а, 5/5.

- (1,66) 2 = 0,307,

05,4) * = 1,7,

Г = - 4,96 • 0,307 / 1,7 = - 0,89.

З розрахунків випливає, що між факторним і результативним приз ¬ накамі існує сильний кореляційний зв'язок; негативний знак коефіцієнта кореляції свідчить про те, що збільшення фак-рного ознаки (потужності пласта) призводить до зменшення результа-тивного (собівартості видобутої корисної копалини).

Визначимо залишкову дисперсію

Рис. 8. Регресійна залежність себестоі-мости від потужності пла ¬ ста:

У 18

17

16

15

14

13 грудня

1 і 2 - відповідно верхня і нижня гра ¬ ниці довірчого ін ¬ інтервалу

\

\ Ч

\

\

\

\ \

4х \) = * 23,63 - <: \ т

ч Ч N \

\

\> V / у2

\

\

про \ \

v \ \ \ \

\

Ч ^ v

\ N

\

\> \ V \> \

\

• \> \

\

\ \

Ч ° 4

\ З

\ N \

\

2,0

1,0 1} 2 /, 4 - 1,6 1,8

 

  

При рівні значущості а = 0,05 для К - п - т - 1 = 10 в табл. 2.13 знаходимо критичне значення статистики Стьюдента / 10.0 05 = »= 2,23. Величина довірчого інтервалу, розрахована у відповід ¬ ності з формулою (2.50), дорівнює

(Х - 1,66) »1,143

V.

1

12

S-t

У (х)

= 1,06

2,23 =

Ю; 0,05

 

  

= 2,364 V0, 083 + 0,875 (* - 1,66) 2.

Відзначимо, що величина довірчого інтервалу мінімальна при х = х і збільшується при відхиленні х відносно х. Графік лінії регресії і відповідний їй довірчий інтервал при ¬ дені на рис. 8.

Оцінимо значущість коефіцієнтів рівняння регресії а0 і аг. Для цього обчислимо дисперсії коефіцієнтів за формулами (2.51) і (2.52)

1 (1,66) 2 12 + 1,143

Si = 1,124

"Про

= 2,8; SQo = 1,67;

 

  

S? = 1,124 / 1,143 = 0,983; Sn = 0,991. «1" 1

Визначимо статистики та й порівняємо їх з критичним значен ¬ ня ^ ю: 0.05 = 2> 23

= 5,0.

14,15; ^ = 5

1,67

\ А0 \ 23,63

аг I _ 4,96 0,991

а про

Оскільки / і ta набагато більше критичного значення, гіпо ¬ тезу про рівність нулю коефіцієнтів регресії відкидаємо і оцінки і ах параметрів а0 і ах функції регресії визнаємо значущими.

За середнім квадратичним відхиленням коефіцієнтів рівняння йія регресії можна оцінити їх довірчі інтервали. З формули (2.46) отримаємо

23,63 - 1,67. 2,23 <сс0 <23,63 + 1,67. 2,23; 19,9 <сс0 <27,35;

- 4,96-0,991 • 2,23 <ах <- 4,96 + 0,991. 2,23;

- 7,17 <0 ^ <-2,75.

Таким чином, оцінювані параметри функції регресії а0 і ах можуть відрізнятися від оцінок а0 і а1, проте з вірогідністю Р = 0,95 їх значення потраплять в довірчі інтервали 19,9 ... 27,35 і -7,17 ... -2,75 Відповідно.

Оцінимо значущість рівняння регресії з використанням дива ¬ стіки Фішера. Виходячи з даних табл. 2.16, отримаємо

<2 = - ПУ2 = 2880,62 - 12. (15,4) 2 = 34,7;

  

Ю;

= 20,87.

Т7 =

0ост / / С2

Оост ^ 11 »24; / сж = 1; / С. = 12-2. ^ - (^ Ост) ^! (34,7 - 11,24) / 1,0

11,24 / 10,0

  

З табл. 2.15 знаходимо критичне значення / ^-статистики при К \ = * = 1, / С2 = 10 і рівні значущості а = 0,05: (1; 10; 0,05) = 4,96. Оскільки Т7;> 4,96, рівняння регресії значимо.

Двофакторна регресійна залежність. Для слу ¬ чаю т = 2 система рівнянь (2.38) записується так:

^ Хі - пх \ ^ + а2 х21Хі - пх2хг ^ =

п

= £ УсХі - пухх, 1 = 1

п

= V

Хі * 21 ~ + а2 ^ х \ I - пх ^ 1 =

Ь У \ хи - пух2.

Матриця № і вектор V відповідно мають розмір ¬ ність 2 X 2 і 2 X 1. Враховуючи, що

(2.53)

п _ п

2 Хі - ПХ \ = 2 х \ I - пх2 =

1 = 1

X ХцХп - пххх2 = п8х18х

£ у ^ м-пух1 = пБххБуГух ^

  

£ у 1 * 21 ■

'Пух2

пЬх ^ уГ ух2у

  

матриці № і V дорівнюють

  

V? =

V

П ^ ХгЗуГ ух, п ^ х2 ^ уГУх2

  

Визначимо зворотну матрицю Г-1. Вона обчислюється за наступним правилом: у вихідній матриці кожен еле ¬ мент замінюють його алгебраїчним доповненням; отриманий ¬ ву матрицю транспонирует; кожен елемент матриці де ¬ лят на визначник вихідної матриці.

Виконавши описані перетворення, отримаємо

  

А2 5 "5" г "

Л | Л2 А1А2

ІГ "1 =

(2.54)

ПЕГ

Х1 Х2 Х \ Х%

пЧЛ ("-О

  

З виразів (2.39) і (2.40) знаходимо формули для визна-поділу параметрів рівняння двофакторної регресії

гчх / ххх ^

а1 = £ 5

1 = 1 Про ~ ~ тххх)

а2 = у Г27V, = 8У {гу *,-г »* г * гхш)

(2.55)

(2.56)

(2.57)

^ Ч м

1 = 1 ^ Хо і

V ч

Рр. г) Х \ Х 2

а0 = у - Аххх - д2х2.

З урахуванням формул (2.44) і (2.45) визначимо розрахункові формули для дисперсій коефіцієнтів регресії

  

1

с2 _ про ° а0 -

п '^ - ^ хх)

х1 х9 ххх2 '

5а, = ^ ост ^ П1 = 0-г2ХгХ2)]>

Х \ Х2 ХуХг

(2.58)

(2.59)

(2.60)

^ = - Зост / І ^, (1-г \ хХш) \.

  

Приклад. Встановимо регресійну залежність змінної произ-водительности праці робітника очисного забою у від потужності пласта х1 і довжини лави х2 по середньомісячним даними, отриманими з звіт ¬ ності за всіма вибоїв шахти.

№ з / п М М у.

т / смен х \ 4 У ** г У ХДУ У (* 1 * 1) У (- У

Вихідні дані і проміжні розрахунки наведені в табл. 2.17. Як випливає з таблиці,

= 15,7: 13 «1,208; х2 = 6,0: 13 = 0,462;] / = 134,1: ​​13 = 10,315;

Їх?

= - = 19,51: 13 - (1,208) 2 = 0,042; = 0,205;

^ = - Х $ = 2,89: 13 - (0,462) а = 0,0089; = 0,094; Еу?

у2 = 1395,13:13 - (10,315) 2 = 0,918; Я «= 0,958;

п "

__ ^ У/Хц/п- ^ х ^ _ 164,19: 13 - 1,208 • 10,315 _ ~ ~ "" 0,205 • 0,958 ~ ~ '

- * 2У __ 62,695: 13 - 0,462 • 10,315 ** ~ 0,094 - 0,958 ~ ~, Ь;

^ Хіх21Ш-х ~ х2 __ 7,33: 13 - 1,208 ■ 0,462 __

0,205 • 0,094

Коефіцієнти рівняння регресії обчислимо за формулами (2.55) - (2.57)

_ 0,958 (0,87 - 0,64. 0,3) 01 "" 0,205 (1 - 0,32) ""

0,958 (0,64 - 0,87 ■ 0,3) _ 0,094 (1-0,32) а0 = 10,315 - 3,48-1,208 - 4,24-0,462 = 4,15.

Таким чином, рівняння множинної регресійної залежністьмости продуктивності праці від потужності пласта і довжини лави має вигляд

Ц (Хг, х2) = 4,15 + 3,48 л:, + 4,24 л: 2.

По рівнянню регресії обчислимо умовну середню у (х'х2) для кожного набору факторних ознак, після чого визначимо залишкову дисперсію (див. табл. 2.17)

п

V (у, - 5 (* ")) ■

= ^ = 0.274.

Обчислимо дисперсії коефіцієнтів регресії, використовуючи розрахунок ¬ ні формули (2.58) - (2.60),

(1,208) 2. 0,0089 + (0,462) 2. 0,042 -

2 п п з [1 - 2. 1,208 - 0,462 - 0,205 - 0,094 - 0, з1 - О, та / 0 13 + 13 0 042 0 ^ 008д (1 __ 0 32)]

= 0,269; = 0,518; 3529 65

= 0,075: (13 • 0,042 (1 - 0,32)) = 0,151; = 0,388; = 0,075: (13. 0,0089 (1 - 0,32)) = 0,71; Я = 0,844. Визначимо статистики 1а і порівняємо їх з критичним значенням а при рівні значущості а = 0,05 і числі ступенів свободи К = »-я-т - 1 = 10 (* 10; о.о5 = 2'23)

  

4,15 0,518

ах

= 8,01; / в | =

/

А>

"Про

= __ 3'48__ = 8,97;

0,388

  

= 5,02. tn

/ =

Оскільки обчислені величини tQn, ta> ta ^ більше критичного значення, оцінки параметрів функції регресії є значущими «Їх довірчі інтервали рівні відповідно

4,15 - 0,518 • 2,23 <сс0 <4,15 + 0,518. 2,23; 2,99 <а0 <5,30; j 3,48-0,388 - 2,23 <ССХ <3,48 + 0,388 • 2,23; 2,61 <з ^ <4,34;

4,24 - 0,844 • 2,23 <СС2 <4,24 + 0,844 • 2,23; 2,36 <а2 <6,12.

Малий обсяг вибірки (п = 13) є причиною того, що дис ¬ Персії коефіцієнтів регресії мають великі значення, через що довірчі інтервали коефіцієнтів великі. Це може призвести до певних неточностей при аналізі отриманих результатів. Пояснимо це положення на прикладі першого фактора. З отриманої регресійної моделі видно, що при збільшенні потужності пласта на 1 м в порівнянні з базовим варіантом продуктивність праці робо ¬ чого очисного забою зростає на 3,48 т за зміну. Однак величина дове ¬ редньо інтервалу для ^ показує, що інші вибірки такого ж обсягу могли дати для коефіцієнта регресії значення в інтервалі 2,61 ... 4,34 і відповідні їм величини приросту продуктивності праці. Таким чином, для об'єктивної і однозначної оцінки влия ¬ ня потужності пласта на продуктивність праці слід звузити дове ¬ редньо інтервал. Це досягається збільшенням обсягу вибірки. Разом з тим з отриманих по даній вибірці результатів можна сде ¬ лать однозначний висновок про те, що збільшення потужності пласта підвищення ефектив ¬ щує продуктивність праці, причому не менше, ніж на 2,61 т за зміну при прирості потужності на 1 м.

Оцінимо значущість рівняння регресії, використовуючи статистику Фішера F.

Виходячи з даних табл. 2.17, отримаємо

_ 4,24

0,844

а 2

Q = 1395,13 - 13 (10,315) «=« 11,94;

= 74,5.

Qoct * 0,7508; Кг = 2; = 13-3 = 10;

(Q-Qoct) / *! Сіє / **

За табл. 2.15 знаходимо критичне значення / ^-статистики при Кг = »* = 2, / С2 = 10 і рівні значущості а = 0,05: (2, 10, 0,05) = 4,1. Оскільки F> 4,1, рівняння регресії значимо, тобто гіпотеза про дорівнює * стве нулю всіх коефіцієнтів регресії відкидається.

Кореляційна матриця взаємозв'язку результативного і фактор ¬ них ознак дорівнює

Г 1,00 0,87 0,64 "Сз = 0,87 +1,00 0,30 | _ 0,64 0,30 1,00 Обчислимо приватні і множинний коефіцієнти кореляції

  

- А

1.2

= 0,925;

УХіХш

- А

= 0,806;

Ух% Х \

0,234

0,678

У 0,91 • 0,59 0,379

1.3

, З, з

У 0,91

У * и

= 0,956.

До УХ хХг =

+ Гух2 ~ ~ 2У1

ГКлХ-2

  

З наведених результатів видно, що насправді кор-ляціонному зв'язок між результативним і факторними ознаками сильніше, ніж це випливає із значень парних коефіцієнтів кореляції; коефіцієнт множинної детермінації Я1 - 0,915, тобто чинники хх і х2 пояснюють 91,5% варіації результативного ознаки.

2.9. Нелінійна регресія

Регресійна залежність може бути нелінійною по факторному ознакою х. Вид цієї залежності зазвичай визначається характером розташування вибіркових точок на кореляційному полі. Проте у ряді випадків несколь ¬ ко різних регресійних моделей (лінійних і нелінійної ¬ них) можуть приблизно з однаковою точністю описувати вибіркові дані (відзначимо, що точність моделі, аппрок-сімірующей залежність результативної ознаки від факторних, оцінюється величиною залишкової дисперсії). При виборі однієї з альтернативних моделей керівництву ¬ ються смисловий адекватністю кожної розглянутої залежності описуваного явища чи процесу. Напри ¬ мір, при вивченні залежності собівартості видобутку від потужності пласта (див. приклад на с. 59) приймалася линів ¬ ва регресійна модель, яка досить добре опи ¬ Сива досвідчені дані в діапазоні потужності 1,2 ... 2,2 м. Однак очевидно, що подальше збільшення потужності пласта не може забезпечити такого ж зниження себестоі ¬ мості, оскільки в кінцевому підсумку можна прийти до абсур ¬ ду: при х> 4,76 м з рівняння регресії отримаємо у (х) <• <0. Як буде показано далі, "модель, що допускає ек ¬ страполяцію в розумному діапазоні варіації потужності пласта, повинна бути гіперболічної.

  

3 *

67

Найменування залежності

Аналітичний вид

Прео разование до лінійного вигляду

  

Гіперболічна

Параболічна

Степенева

Показова

Експоненціальна 1

Показово-

статечна

Експоненціальна 2

Зворотній лінійної

Зворотній гіг.срболі-чгской

Зворотній параболи-ческой

у = а0 + ах / г

у = а0 + ахх + а2х2 у = АЦХ * 1, У = У =

у = а *

(/ = А "4 - а-, ^" У = 1 / (ао +

у = 1 / (а • ■)

у = 1 / (а, -

1, ш = -; у = а0 + Ахт)

хх = х \ х2 = х2 \ у = а0 + а ^! + А ^ у = 1п і> = \ п х; А0 = 1п а0; V - А0 + Ахт V = 1п у \ Лз = 1п а0; Ах = 1п ах; V = Л0 + у = 1п у; А0 = 1п а0; 1> = Ап + ахх

У = -; Біля:

У

і = гю - їх V = а0 + пекла г2 * а) у = 1 / в; д ^! = * 2 = х2 \ V = а0 + а ^ + а2 * а

і = 1п у \ Ап = 1п а0; ні = \ п х-А2 = 1п а2; V = А0 + ах »+ Агх

= *; У = а0 +

I

а "+ агх

  

Таблиця 2.19

Зворотні перетворення змінних і параметрів

Найменування залежності

Сис ем,, чрнв Еч! • д.т чичіслені * параметрів

 

  

па0 Н-ах'і) 1 =

X = 1 / ш

Гіперболічна Параболічна

х - хх X2 = * 2

+ АХ1> хю \ -'у {іо1 па0 + ах1ххс + а2'х21 = 2у {А02 хі + а, + а21хіх21 =

Степенева (пА0 + =

Показова

\ Л02а ^ + а ^ і ^ = 21707

(АЛ0 + Ах'х1 = \ Л02 ^ + = 2 ^ *,

  

Експоненціаль-ная 1 (пА0 + ах2х1 = 2 VI \ AolXi + ах 2 ^ =

  

Показово-статечна

Експоненціаль-ная 2

Зворотній линів ¬ ної

ПАЩ + 0x2 ^ + А2 2 * / = 2 »*, Лв2ю £ + + = 21707,

Л02л:, + ^ 2 ^ + Л2 2 *? = 2 »^

Глав + а ^ а ;/ = \ а02а7 + ах2а>? = /

Гла0 + Дх2 ** = 217, (А02 ^ + ^ 2 *? = 2 ^

  

Зворотній гіпер-боліческой (па0 + а12а> г = 2 ^, | а02ш / + ^ 210? =

  

Зворотній парабени-вої

{

па0 + аг2хц + а21х2 {= 2 ^, а0 2хг, + ат 2 * ^. + Аа2 * 1! * 2 / = А02 * ц + Ч 2Х1СХ21 + а22д ​​^. = 2 ^

у = eü, л: = tm

ае = Верб

у = е °, fl0 = є "» ах = їв °

у = е °, а0 = е ^ у = е °, * = Еш

а ® = І »

X =-In а>

* = I / o

у = I / o, X = 1 / ю

XІ = X,

I / o

Найбільш часто вживані в практиці статистичних розрахунків нелінійні регресійні залежності, а також їх перетворення, що дозволяють використовувати метод наи ¬ менших квадратів, наведено в табл. 2.18. Система урав ¬ нений для визначення параметрів регресійної моделі складається щодо залежності, перетвореної до лінійного вигляду; після рішення системи рівнянь виконується зворотне перетворення від допоміжних величин до початкових (табл. 2.19).

Приклад 1. Встановимо гіперболічну регресійну залежність собівартості 1 т вугілля у від потужності пласта корисної копалини х при умовах, наведених у прикладі на с. 59. Вихідні дані і про-проміжні розрахунки представлені в табл. 2.20.

Для визначення шуканих параметрів О0 і ах складаємо слідую ¬ щую систему рівнянь:

(1200 + 7,5080! = 184,8,

\ 7,50800 + 4,8710! = 117,695.

Вирішення цієї системи: О0 = 7,683; аг = 12,046.

Таким чином, залежність собівартості вугілля від потужності пласта можна представити рівнянням регресії виду

у (х) = 7,863 + 12,046 / *.

Обчислимо коефіцієнт кореляції

з с Л ^ -2 г / * 4> 871 / 7,508 \ а - 100 -

X

Таблиця 2.20

  

-До 9 *

& 1ч

*

нГн * і

§ г см

3 із § г

1 = 5> 1

АГ

в

До

§

 

0,487 4,219 0,510 0,059 0,011 0,019 1,590 1,938 0,392 0,113 0,162 0,225

15,898 14,946 13,886 13,344 13,597 14,561 14,561 15,392 17,126 16,464 17,897 17,126

-0,698 2,054 0,714 -0,244 0,103 0,139 -1,261 -1,392 -0,626 0,336 0,403 0,474

10,138 9,996 7,300 5,961 6,521 8,173 7,395 8,750 12,688 11,995 15,244 13,534

0,445 0,346 0,250 0,207 0,227 0,309 0,309 0,391 0,591 0,510 0,694 0,591

15.2

17.0

14.6

13.1

13.7

14.7

13.3 14,0

16.5

16.8 18,3

17.6

0,667 0,588 0,500 0,455 0,476 0,556 0,556 0,625 0,769 0,714 0,833 0,769

1.5

1.7 2,0 2,2 2,1

1.8 1,8

1.6

1.3

1.4 1,2 1,3

2 Січень

3

4 б 6

7

8

9

10 11 12

 

  

9,725

2 184,8 7,508 4,871 117,695

Sy = 1,7 (див. приклад на с. 59);

Ü и

= 12,046

= 0,868.

0,1225 1,7

  

З розрахунків випливає, що між результативною ознакою і обрат ¬ ної величиною факторного ознаки існує сильний кореляційний ¬ ная зв'язок; коефіцієнт детермінації дорівнює 0,753. Обчислимо залишкової ¬ ву дисперсію. Виходячи з даних табл. 2.20, отримаємо

  

9,725

З 2 _

ост -

10

п - т - 1

= 0,9725; 5ост = 0,9861.

  

Гіперболічна і лінійна регресійні залежності себестоі-/ мости вугілля від потужності пласта наведено на рис. 9. Зіставляючи резуль-тати даного прикладу з результатами прикладу на с. 59, відзначимо, що кореляційний зв'язок результативної ознаки з факторним приблизно одна і та ж як для лінійної, так і для гіперболічної моделей. Однак для гіперболічної регресії менше залишкова дисперсія, що свідчить про більший відповідності цієї моделі спостережуваним фактам.

Приклад 2. Визначимо параметри рівняння регресії, відображаю ¬ ного залежність коефіцієнта машинного часу механізований ¬ ного комплексу у від довжини лави х. Вихідні дані для розрахунку при ¬ дені в табл. 2.21.

Кореляційне поле і емпірична лінія регресії показані на рис. 10. Для побудови цієї лінії діапазон значень факторного ознаки розбитий на / г = 5 інтервалів (К - 1 + | 3,32 1 § 23 [= 5). У кожному інтервалі обчислено середнє значення результативного приз ¬ нака (зазначено на графіку в середині інтервалу). Поєднавши отримані точки ламаної, отримаємо емпіричну лінію регресії, характер

  

N ч і г) = 7,86 Ї i + rzfc tf / r

N {23,63 - ШХ

X

про \

N

> Ч «

N

17

16

1,0 1,2 (4 (6; а 2, про х Рис. 9. Зіставлення линів ¬ ної і гіперболічної моді ¬ лей собівартості 0,35 0,33 0,31 0,29 0,27 0f25 0,23 0 , 21

0,10 0,12 0,14 0,16 0,18 0,20 0,22 x10 '

1

і h-

\

1 січня

1, О и 1 січня

1 У и у? 1

1 січня

/ 1

/ J 1 Про 1 1 1

1

~ I 1

1

4] 1 1 1 1 1

\ \ 1 -

I

1 1 1

1.

Рис. 10. Кореляційне поле і емпірична лінія регресійної залежності коефіцієнта машин ¬ ного часу від довжини лави

Ф ^ cd ^ - ^ іл-^ ої - <про <ососоо> про> д ^ ^ ю-<з - про>

<N

Про

рр.

1

g

<»Сосооадсо ^ ^ сососм ~ ^ ооююоосо ^ а> ем0 ^ WqNq-wqqoooo соо ^ юо - ооо

  

SS2

н

I = >>

00 CD <N - OilOOOS

-, - ^ TfCDTfr ^-COCOtNin - ^ - СО

ОООЮ - 00 СМ СО - «OiOQCOCMCMf-O ^ OQ ~ Q« - <0000 - '-1О-О О - • О - О - ТОВ оооооооооооооооооооо

ооооороооооооооооо

  

s

СЧ СЧ (N СЧ СЧ СЧ СЧ СМ СМ СЧ СЧ СМ <N <N СО_ ГО СО СО СО СО СО СО_ ​​СО

& И

CM <Nh-a> a> io <NcD

про "про про" про про про "про" про про "про" про про про "про" про "про" про ~ про про "про про" про про "

оесо ^ счо ^ сосмоооюсог-'-ю ocMCMOf-^ oio - соСоюг «-

^ ^ ^ CO ^ Th '^ LOCDCDCD ^ OOOOO ^ ^ ^ COlibcDh ^ oo

про ПРО Про про про "про" про "Про про" про "Про про" Про про "-"-г-Г ~ -4

  

 

& Ц

  

- J CD - rt «(M CM 00 Про CM - CM 00 CD ^ (M

JNO ^ OOWCvjTtcûCOOïiOiniOOi'-'MOIN'tOlOOO) Про Сол CD 00 1С 00 ^ о СО СО iD СО ^ сож ^ h * Про ^ f - ^ СО_ ^ en Tf-СЧ С \ Г CM З \ Г СМ ~ СО зі "Ю ю" CD CD ГО ГО про "-СО Qï СО h-Г 0 ~

-Сча) - COCOlOcOOOTfCDN ~ '"l СЧ CM CM CM СО CO_ rf LO CD CD t ^ 00_ C> O ^ CM ^ CM ^

0 ~ o ~ 0 ~ про про "про про про про про про про" про "про про про про" про про "про ~ - ~

^ Зі CD ооо> см з

<N зі СО ^ CD ю 1Л CD 00 Про f-О oo О - СО СМ *

CMCMCMCM <NCM <N <NCM <N <NCMCMCOCOCOCOCOCOCOCOCOCO

- • ~ ~-Г-Г ~ - <"<n см" см "см" см "см" зі зі "зі" зі "^ rf ю" 1С

«СМ Ю Tf зі ^ ^ ^ 00 00 00 00

г>

- Я

про про про про про про про про про "про про про про про про про про про" про "про" про "про" про "

OOtlOOOONOQWOlQOOOiOOCOtOOOlO

^ ^ ^ ^ Смсосо ^ СбююФ ^ ^ ооадфФо ^ з ^ Сосо про про про про ~ о о о ~ про про "про про про про про про про ~ про ~ про про про про про про

  

f *

проведення якої свідчить про те, що залежність між приз ¬ накамі слід описувати параболічної регресійної моделлю. Враховуючи, що

Хх Як дс, х2 = х2, ххх2 -, х2х2 - х *, ух! = Ух, УГГ = ух2,

для знаходження шуканих параметрів а0, 0 |, а? складаємо систему рівнянь за даними табл. 2.21

(23а0 + 3,825 ^ + 0,6668 а2 = 6,6, | 3,825 а0 + 0,6668 а, + 0,12145 а2 = 1,12855, 1 0,6668 ат + 0,12145 «! + 0,022997 а2 = 0,201783.

Вирішення цієї системи: а0 = -0,0582; ах = 3,1713; а2 = - 6,286. Отже, залежність коефіцієнта машинного часу від довжини лави можна представити таким рівнянням регресії:

~ У (х) = -0,0582 + 3,1713 Л: - 6,286 Л: 2.

Зіставивши розрахункові значення у (х) з табл. 2.21 з відповідним-ські їм значеннями на емпіричній лінії регресії, неважко переконатися-диться в їх відповідності. Залишкова дисперсія дорівнює

  

Комерсант (У1 - 21,8661 • 10 '

■ 4

= 1,0933 • 10 ~ 4.

п - т-1 ~ ~ 23-2-1

 

 

  

Відзначимо, що, незважаючи на наявність одного факторного ознаки (довжина лави), при визначенні числа ступенів свободи було прийнято т 2. Це пояснюється тим, що параболічна регресія була зведена до лінійної двофакторної {хг = х, х2 - х2) і тому число накладено ¬ них зв'язків приймалося рівним двом.

2.10. Аналіз рівняння регресії

Рівняння регресії дозволяє встановити характер впливу факторних ознак на результативний.

За знаком коефіцієнта регресії ак визначається на-правління впливу ознаки хк на результативний при ¬ знак: позитивний знак вказує на зростання іс ¬ належної величини при збільшенні фактора ГКУ отрица ¬ вальний - на ее4 зменшення.

Абсолютне значення коефіцієнта регресії ак поки-показують, на скільки одиниць збільшиться (зменшиться) резуль-татівний ознака при збільшенні факторного на одиницю (див. приклад на с. 63).

Багатофакторне рівняння відображає вплив несколь ¬ ких факторних ознак на результативний. Якщо необ ¬ хідно виділити вплив фактора хк при фіксованих значеннях інших факторів, то з рівняння безліч ¬ ної регресії отримують рівняння чистої регресії. Для "того всі фактори, крім хк> прирівнюють до їх середнім

рівнями і отримані значення підставляють у рівняння множинної регресії.

Методику побудови рівняння чистої регресії рас-дивимося на основі даних прикладу, наведеного на с. 63. Отримано рівняння множинної регресії

у (х'х2) = 4,15 + 3,48 *! + 4,24 х2, де у - продуктивність праці робітника очисного за ¬ бою, т / зміну; ^ - потужність пласта (хх = 1,208), м; х2 - довжина лави (х2 = 0,462), 103 м.

Рівняння чистої регресії продуктивності праці в залежності від потужності пласта має наступний вигляд:

у (х1/х2 = ~ х2) = 4,15 + 3,48 ^ + 4,24. 0,462 =. = 6,109 + 3,48 ^.

У цьому рівнянні виключено вплив на виробник ¬ ність праці довжини лави. За формою чиста регресія похо ¬ жа на парну, проте відрізняється від неї за ступенем точ ¬ ності. Можна уявити собі ідеалізований експе ¬ рімент, в якому визначають статистичні дані про продуктивність праці при різних потужностях пласта, але при довжині лави, рівної її середньому рівню х2. Отримано ¬ ва за результатами цього експерименту вибірка дозволить встановити рівняння парної регресії, еквівалентне даного рівняння чистої регресії.

Аналогічно складемо рівняння чистої регресії произ-водительности праці в залежності від довжини лави

у (х2/Х1 = хх) = 4,15 + 3,48 • 1,208 + 4,24 л: 2 == 8,354 + 4,24 * 2.

У цьому рівнянні виключено вплив на виробник ¬ ність праці потужності пласта.

Відносне кількісний вплив факторного при ¬ знака на результативний оцінюють за допомогою коефіцієнта ¬ ента еластичності, який показує, на скільки про ¬ центів змінюється рівень результативної ознаки при зміні факторного на один відсоток.

Коефіцієнт еластичності визначають за формулою

(2.61)

* У (Ч)

де хк - значення к-го факторного ознаки, при якому визначається коефіцієнт еластичності; біля {хк) - значе ¬ ня результативної ознаки при відповідному зна ¬ чении розраховане за рівнянням чистої регресії.

Для лінійної регресійної моделі

<4 - Ао + аьхь а * '

де

к-1 _ т _

= 7 а0 + Е аг * г + Е аг * г-

г = 1 г-до-\ - \

Для параболічної регресії

е * = а "+ + +

З наведених формул видно, що коефіцієнт Елас-тичності динамічний і його значення визначається рівнем фактора, при якому він розраховується. Зазвичай коефі ¬ ціент еластичності обчислюють при середніх рівнях ре ¬ результативності і факторного ознак.

Використовуючи отримані вище рівняння чистої регрес ¬ ці та беручи до уваги, що у = 10,315, визначимо коефіцієнти еластичності продуктивності праці по факторним ознакам

З даних значень коефіцієнтів еластичності сле ¬ дует, що зміна потужності пласта на 1% призводить до зміни продуктивності праці на 0,41%; зраді ¬ ня довжини лави на 1% викликає зміну виробляй ¬ ності праці на 0,19%. Отже, ранжуя фактори по їх впливу на результативний ознака, потужність пласта поміщаємо на перше місце, а довжину ла ¬ ви-на друге.

При управлінні гірничими роботами можна виділити за допомогою коефіцієнтів еластичності найбільш сущест ¬ ються фактори і, варіюючи ними перш за все, обеспечи ¬ вати оптимальний режим роботи.