2.4. Поняття регресії

Дослідження залежності між випадковими зміннимі - факторним ознакою X і результативним признаком Y - на практиці обмежують вивченням залежності між X і умовним математичним очікуванням М (Y / X = х ) = (М), де М (Y / X = х) - математичне сподівання випадкової величини Y за умови, що випадкова величина X прийняла значення х. Ця залежність отримала назву функції регресії Y на X.

Для визначення функції регресії треба встановити аналітичний вигляд двомірного розподілу f (У, X). Однак практично це зробити досить складно, ocкільки дослідник зазвичай розпорядженні вибіркою обмеженого обсягу, по якій з однаковим ступенем точності сукупність даних (x_i,y_i)i = 1, 2, ..., n можна описать різними функціями. Тому в практиці статистичних розрахунків при вивченні залежності між X і Y використовують поняття емпіричного рівняння регресії, або просто рівняння регресії.

Емпіричне рівняння регресії Y по X (або Y на X) встановлюють за спостережуваними значеннями двомірної випадкової величини (х, у) у вигляді виразу (х) = (х, а₀, a_l, ..., а_m) де (х) - умовне середнє значення випадкової змінною Y, яке визначається за емпіричними даними; а₀, а₁ ... a_m - параметри рівняння регресії, які визначаються методом найменших квадратів.

Таким чином, функція регресії М (Y / X = х) = (х) може бути визначена для генеральної сукупностіності (X, У), рівняння регресії-для вибірки обмеженого обсягу (x_i,y_i), i = 1, 2, ..., n.

Функцію регресії представимо у вигляді

М (У / Х = х) = (х) = а₀ + а₁x+a₂x²+… +a_mx^m (2.17)

де а₀, а₁, а₂, ..., а_m - коефіцієнти регресії.

Оскільки досліднику не відома вся генеральна сукупність даних, за вибіркою визначається рівняння регресії

(х)= а₀ + а₁x+a₂x²+… +a_mx^m (2.18)

Параметри рівняння регресії а₀, а₁, а₂, ..., а_m являются оцінками коефіцієнтів регресії α₀, α ₁, α ₂, ..., α _m. Завдання регресійного аналізу полягає в обчисленні цих оцінок. Надалі, там, де мова буде йти про рівняннях регресії, оцінки коефіцієнтів регресії також будемо називати коефіцієнтами регресії.

Крім оцінки коефіцієнтів регресії, оцінюється залишкова дисперсія - розсіювання результативної ознаки щодо умовного математичного очікування М (У / Х = х). У регресійному аналізі такої оцінки є вибіркова залишкова дисперсія, визначається по формулі

(2.19)

де n - кількість даних у вибірці; m + 1 - кількість параметрів в рівнянні регресії.

Залишкова дисперсія може використовуватися для аналізу і оцінки точності підбору функції регресії. Надалі (див. розділ 2.8) це питання буде вивчений докладно, а в даному розділі зупинимося на розгляді лінійного рівняння регресії.

У регресійному аналізі найбільш широко виконується нормальна регресія, основною передумовою якої є виконання умови, що {У / Х = х) - множина значень У при X = х - підпорядковане нормальному закону розподілу. У цьому випадку оцінки коефіцієнтів регресії підпорядковані нормальному закону розподілу з мінімальною дисперсією, що дозволяє знайти для них довірчі інтервали та оцінити їх значущість. Припускаємо, що надалі умови нормальної регресії виконуються.

Лінійна регресія має місце в тому випадку, якщо функція регресії (2.17) лінійна, тобто М (У / Х = х) = а₀ + а₁х.

Лінійної функції регресії, що є для генеральної сукупності моделлю залежності між факраторних і результативним ознаками, відповідає ліниве рівняння регресії (х)= а₀ + а₁x₁ параметри якого а₀ і а₁ визначаються за вибірковими даними з умови мінімуму суми квадратів відхилень емпіричних значень результативної ознаки від обчислених по рівнянню регресії

F= =(y_i - а₀ - а₁x₁) →min

Значення параметрів а₀ і а₁ звертають в мінімум функцію F знайдемо з рішення системи рівнянь

Виконаємо диференціювання

Після рівнянь нескладних перетворень одержимо систему

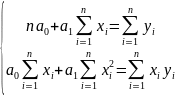
Вирішуючи цю систему відносно а₀ і a₁ отримаємо оцінки коефіцієнтів регресії і 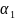. Для вирішення використовуємо формули Крамера. Визначники системи рівнянь рівні відповідно

  

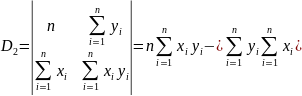
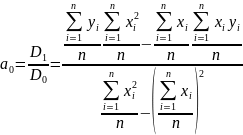
Неважко помітити, що

, ,

Враховуючи ці позначення, отримаємо

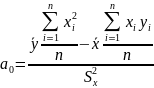(2.21)

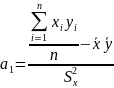(2.22)

Обсяг обчислень можна скоротити, якщо, використовуючи перше рівняння системи (2.20), висловити а₀ через а₁

а₀ = – а₁ . (2.23)

Таким чином, послідовність обчислень зводиться до визначення а₁ за формулою (2.22) і потім а₀ за формулою (2.23).

Оцінку залишкової дисперсії відповідно до формули (2.19) визначимо наступним чином:

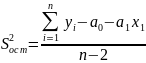
Приклад. Встановимо залежність між собівартістю 1 т вугілля у і продуктивністю праці робітників x по середньомісячним даним, отриманим на підставі статистичної звітності шахти за рік.

Вихідні дані і результати проміжних розрахунків наведені в табл. 2.11.

За даними таблиці отримаємо

= 44,583; = 14,875; = 654,28;

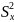= =2018,92 - (44,583) ² = 31,28.

Таблиця 2.11

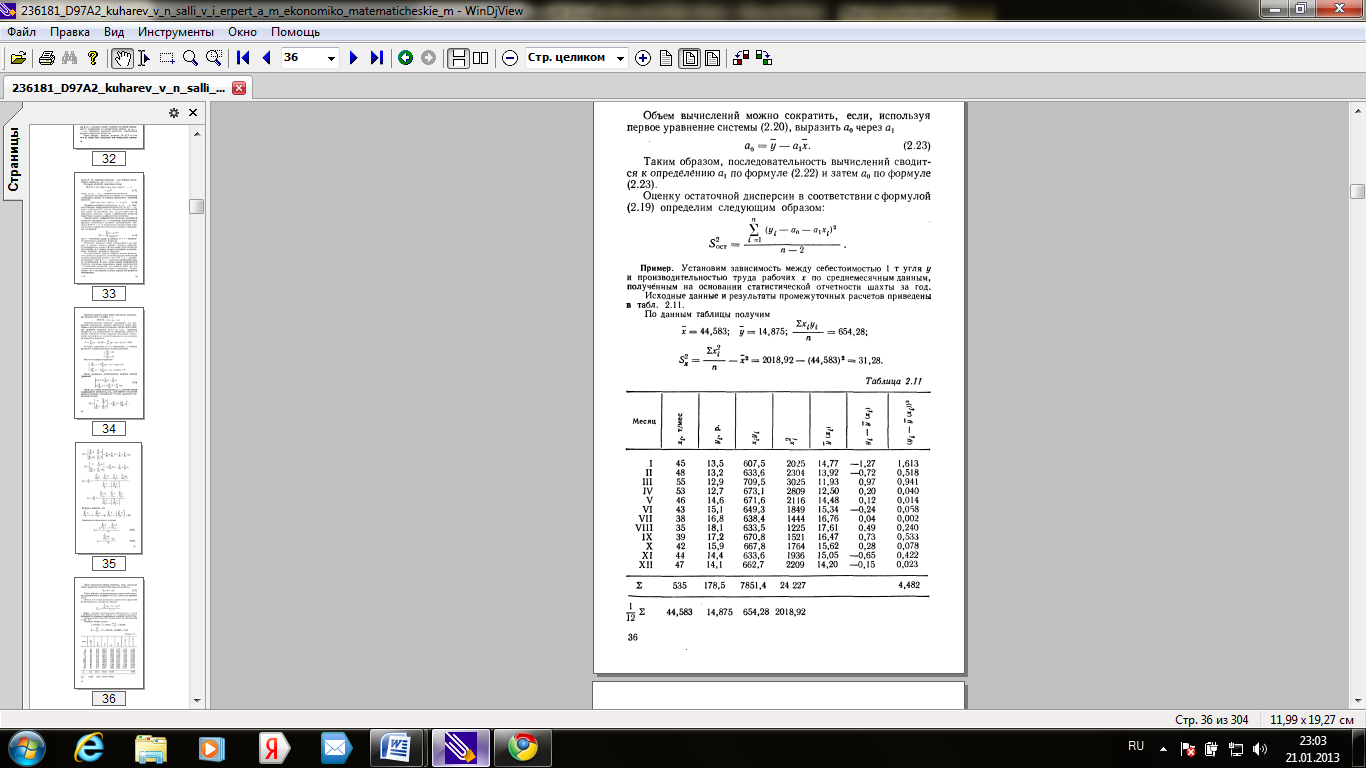
Визначимо параметри лінійногo рівняння регресії а₀, і а₁ відповідно за формулами (2.22) і (2.23)

Рис. 4. Залежність собівартості вугілля від виробничої праці робітників

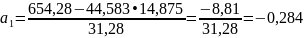
Дані рівняння 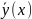= 27,548-0,284x.

Вихідні дані і графік емпіричного рівняння регресії наведені на рис. 4. З малюнка видно, що залежність собівартості вугілля від продуктивності праці робітників в діапазоні спостережуваних значень х досить добре апроксимується лінійною залежністю. Негативний коефіцієнт регресії а, свідчить про те, що із збільшенням факторної ознаки х результативний ознака у зменшується. У даному прикладі збільшення продуктивності праці робітника на 1 т / міс вибуває зниження собівартості 1 т вугілля на 0,284 р.

У трьох останніх графах табл. 2.11 приведені дані для визначення залишкової дисперсії