Рекомендации по оформлению работы:

Оформление работы производится в стандартном стиле и включает следующие пункты;

Лабораторная работа № (номер работы). (Название работы).

Тема работы: (определить тему выполняемой работы).

Цель работы: (определить цель выполнения работы).

Введение

Во введении дать краткое объяснение сути выполняемой работы.

Индивидуальное задание к работе:

Записывается условие данной задачи.

Решение:

Приводится алгоритм составления задачи и конечный набор формализованных условий. Далее приводится выписка из электронной таблицы Excel, соответствующая выполненному решению.

Выводы:

Записываются выводы по приведенному заданию и решению.

Лабораторная работа № 5. Одномерные задачи оптимизации.

Тема работы: Одномерные задачи оптимизации.

Цель работы: Ознакомиться с методами аналитического решения задач одномерной оптимизации и реализацией решения этих же задач в электронной таблице Excel.

Bведение

Приведенная ниже задача имеет широкое практическое применение как частный вопрос при конструировании емкостей для хранения различных продуктов, включая хранилища для нефтепродуктов, элементы очистных сооружений, химические реакторы и др. В упрощенном представлении ее можно назвать задачей об оптимизации размера консервной банки.

Пусть требуется провести оптимизацию емкости для хранения продуктов в форме цилиндра. Можно рассмотреть два варианта оптимизации.

1. Банка должна иметь наименьшую поверхность при данном объеме.

2. Длина свариваемых швов должна быть минимальной.

Аналитическое решение задачи.

Для начала запишем формулы для определения объема банки V, площади ее поверхности S и длины швов l.

V = r²h; S = 2r² + 2rh; l = 4r + h. (1)

Выразим высоту банки через ее объем и радиус h=V/(r²) и подставим это выражение в формулы для поверхности и длины швов.

S(r) = 2r² + 2V/r, 0 < r <  (2)

l(r) = 4r + V/(r²) , 0 < r <  (3)

С математической точки зрения задача о наилучшей форме банки сводится к определению такого значения r, при котором при заданном объеме достигает своего наименьшего значения в одном случае функция S(r), в другом - l(r).

Решение первого варианта задачи. Вычислим производную функции S(r).

S’(r) = 4r - = (4)

Если 2r³ = V, то производная S’(r) = 0, а значение r = . Если 0 < r < r₁ = , то производная S’(r) < 0 и функция S(r) убывает. Если r₁ < r < , функция S(r) возрастает. Значит в точке r₁ = функция S(r) достигает своего минимального значения.

Определим, как соотносятся r и h при минимуме функции S(r).

r = . = ; r³ = ; h = 2r.

Итак, условия, при которых площадь поверхности банки при заданном объеме будет минимальна, определяются формулами:

r₁ = , h₁ = 2r₁ (5)

При этом S(r₁) = 3  S(r) (6)

Определить оптимальное значение r при заданном V можно графически, или с помощью надстройки “поиск решения” электронной таблицы Excel.

Решение задачи по второму условию.

Возьмем производную по r от функции l(r):

l’(r) = 4 - . (7)

Как в предыдущем примере, при 0 < r < r₂ = , производная l’(r) < 0 и функция убывает, если r₂ < r < , функция l(r) возрастает. Определим, как соотносятся r и h при минимуме функции lr).

r = . = ; r³ = ; h = 2r.

Условия, при которых длина шва при заданном объеме будет минимальна, определяются формулами:

r₂ = , h₂ = 2r₂ (8)

При этом l(r₂) = 3  l(r)

Из полученного решения следует, что оптимизация по различным критериям дает разные результаты.

Задача по раскрою.

Из квадратного листа жести со стороной a требуется сделать открытый сверху ящик возможно большего объема , вырезая квадратные уголки и загибая жесть.

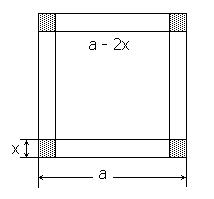
Решение.

Если сторона вырезаемого квадрата равна x, тогда сторона квадрата, образующего дно ящика, равна a-2x. Объем ящика

V = (a-2x)²x = a²x – 4ax² + 4x³.

Для решения задачи нужно найти наибольшее значение функции в интервале ] 0, a/2[. Найдем производную V` = a² – 8ax + 12x².

Приравниваем производную к нулю и решаем неприведенное квадратное уравнение, используя стандартные формулы, по которым для уравнения вида ax² + bx + c = 0; x =

. x₁ = ; x₂ = a/6. Имеет смысл значение x₂.

Находим вторую производную V’’ = 24x – 8a. При x = a/6 V’’ = 24a/6 – 8a = 4a - 8a = -4a < 0.

Значит в точке x= a/6 объем достигает максимума.

.

Задание к работе.

1. Для задачи 1 построить графики зависимостей S(r), l(r) при постоянном V.

2. Определить оптимальные значения r для двух условий решения (заданный объем при минимальной площади поверхности, заданный объем при минимальной длине швов) с помощью надстройки “поиск решения”.

3. К задаче 2 построить зависимость V(x) на интервале x = a/10  a/4 при различных значениях длины стороны исходного квадрата, те есть, величины a.

Варианты задания

Номер Варианта	1	2	3	4	5	6	7	8
Объем цилиндра V, длина стороны квадрата a, у.е.	10	20	30	50	80	110	200	250