Лабораторная работа № 2. Графическое решение задач линейного программирования.

Тема работы: Решение задач линейного программирования графическим методом.

Цель работы: Ознакомиться с графическим методом решения задач линейного программирования. Решить собственный вариант задачи линейного программирования.

Теоретическое введение

На практическом примере рассмотрим графический способ решения задачи линейного программирования (ЛП). Данная задача относится к задаче об использовании ресурсов.

Мебельная фабрика выпускает стулья двух типов. На изготовление одного стула первого типа, стоимостью 8р., расходуется 2 м. досок стандартного сечения, 0,5 м² обивочной ткани и 2 чел./ч рабочего времени. Для стульев второго типа аналогичные данные составляют: 12р., 4м, 0,25 м² и 2,5 чел./ч. Допустим, что в распоряжении фабрики имеется 440 м досок, 65 м² обивочной ткани, 320 чел./ч рабочего времени. Какое количество стульев каждого типа надо изготовить, чтобы в рамках этих ресурсов стоимость произведенной продукции была максимальной?

Решение:

Обозначим через х₁ и x₂ а запланированное к производству число стульев соответственно первого и второго типов. Ограниченный запас сырья и трудовых ресурсов означает, что х₁ и x₂ должны удовлетворять неравенствам:

2x₁ + 4x₂  440

0.5x₁ + 0.25x₂  65 (1)

2x₁ + 2.5x₂  320

По смыслу задачи, переменные x₁ и x₂ должны быть неотрицательными:

x₁  0, x₂  0 (2)

Целевая функция определяет стоимость запланированной к производству продукции и выражается формулой:

f(x₁, x₂) = 8x₁ + 12x₂ (3)

Решение составленной задачи определения оптимального плана продукции по ее сводится к определению пары целых чисел х₁ и x₂, удовлетворяющих линейным неравенствам (1), (2) и дающих наибольшее значение линейной функции (3). Это типичная задача линейного программирования.

Для анализа задачи введем на плоскости декартову систему координат х₁, x₂. Найдем на этой плоскости множество точек, координаты которых удовлетворяют условиям (1), и (2). Неравенства (2) означают, что это множество лежит в первой четверти.

П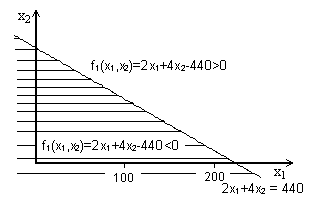 роведем на плоскости прямую, определяемую уравнением

2x₁ + 4x₂ = 440 (4)

(Рис. 1). Она делит плоскость на две полуплоскости. На одной из них, расположенной ниже прямой (4), функция f(x₁, x₂) = 2x₁ + 4x₂ - 440 принимает отрицательные значения, на другой, расположенной выше прямой (4), - положительные.

Рис. 1. Решение неравенства 2x1 + 4x2 <= 440

Первое из неравенств (1) выполняется на множестве точек, которое включает в себя прямую (4) и полуплоскость, расположенную ниже этой прямой. (Заштрихованная часть плоскости на Рис 1). Аналогично можно найти множества точек, удовлетворяющих второму и третьему неравенствам из системы (1). Возьмем пересечение трех найденных множеств и выделим его часть, расположенную в первой четверти. В результате получим множество точек, удовлетворяющих всей совокупности ограничений (1), (2). Данное множество имеет вид пятиугольника, показанного на Рис. 2. Его вершинами являются точки пересечения прямых,.на которых неравенства (1), (2) переходят в точные равенства. Координаты вершин пятиугольника указаны на Рис. 2.

Л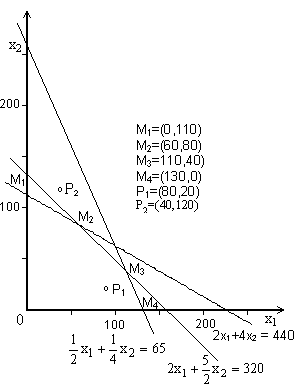 юбой точке Р с целочисленными координатами х₁ и x₂, принадлежащей данному пятиугольнику, соответствует план выпуска стульев, который может быть выполнен при имеющихся запасах сырья и трудовых ресурсов (реализуемый план).

Рис. 2. Пятиугольник 0M1M2M3M4, точки которого удовлетворяют системе неравенств (1), (2).

Если точка Р не принадлежит пятиугольнику, то соответствующий план не может быть выполнен (нереализуемый план).

Рассмотрим на плоскости х₁, x₂ линии уровня целевой функции (3):

8x₁ + 12x₂ = С (5)

Это уравнение описывает семейство прямых, параллельных прямой

8x₁ + 12x₂ = 0 (6)

При параллельном переносе этой прямой вправо параметр С возрастает, влево - убывает.

С войства функции (3) тесно связаны с прямыми (5). Вдоль каждой из них она сохраняет постоянное значение, равное С, а при переходе с одной прямой на другую ее значение меняется. Если рассматривать только первую четверть, а это условие определяется неравенством (2), можно обнаружить, что при переходе от одной прямой на другую значение функции (3) будет тем больше, чем дальше такая прямая удалена от начала координат.

Рис 3. Возрастание функции f(x₁, x₂) = 8x₁ + 12x₂ при переходе от точки Р₁ к точке Р₂.

О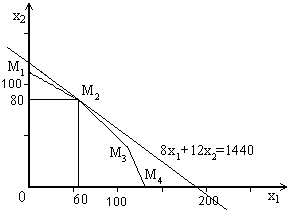 тсюда следует решение задачи: оптимальный план должен располагаться на прямой семейства (5), наиболее удаленной от начала координат.

Рис. 4. Определение оптимального плана производства стульев.

На Рис 4. воспроизведен пятиугольник реализуемых планов и нарисована прямая семейства (5), проходящая через точку М₂ с координатами (60, 80). Она является предельной прямой семейства, имеющей общую точку с пятиугольником. При переносе пямой еще дальше от начала координат мы получим прямую, не имеющую общих точек с пятиугольником, т.е. соответствующие планы нереализуемы.

Полученный оптимальный план предписывает производство 60 стульев первого типа и 80 стульев второго типа. Стоимость этой продукции 1440 р. На выполнение плана нужно затратить: 440 м досок, 50 м³ обивочной ткани, 320 чел./ч рабочего времени.

Оптимальный план требует полного использования запаса досок и трудовых ресурсов, в то время как обивочная ткань будет израсходована не полностью - останется 15 м².

Точка М₂, определяющая оптимальный план, является вершиной пятиугольника. Она лежит на пересечении прямых

2x₁ + 4x₂ = 440

2x₁ + 2.5x₂ =320

Уравнения этих прямых получаются из первого и третьего условий системы (1) при замене их на строгие равенства. Это означает полный расход досок и трудовых ресурсов. Однако точка М₂ не принадлежит прямой 0.5x₁ + 0.25x₂ = 65, так что второе условие (1), связанное с ограниченным запасом обивочной ткани, имеет в ней форму неравенства 50<65. Проведенный анализ показывает, что дальнейшее увеличение стоимости продукции регламентируется запасом досок и трудовыми ресурсам

Задания для индивидуального решения задачи ЛП графическим методом.

Графическим методом найти максимум и минимум линейного функционала f(x) при заданных ограничениях

1. f = 50x1 + 25x2 x1 + 3x2  8 3x1 + 4x2  19 3x1 + x2  7 x1, x2  0	2. f = -x1 + x2 2x1 - x2  4 x1 - 2x2  2 x1 + x2  5 x1, x2  0	3. f = x1 + 2x2 4x1 - 2x2  12 -x1 + 3x2 = 6 2x1 + 4x2 = 16 x1, x2  0
4. f = x1 + x2 x1 - 2x2  14 -5x1 + 3x2  15 4x1 + 6x2  24 x1, x2  0	5. f = -2x1 + x2 3x1 - 2x2  12 -x1 + 2x2  8 2x1 + 3x2  6 x1, x2  0	6. f = x1 + x2 2x1 + 4x2  16 -4x1 + 2x2  8 x1 + 3x2  9 x1, x2  0
7. f = 3x1 + 5x2 0.8x1 + x2  10 0.5x1 + 0.6x2  9 0.25x1 + 0x2  1.25 x1,x2  0, целые	8.	9.
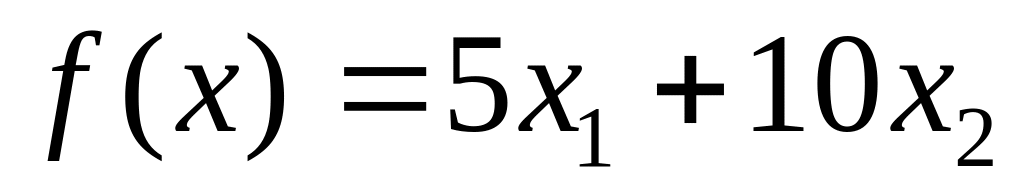
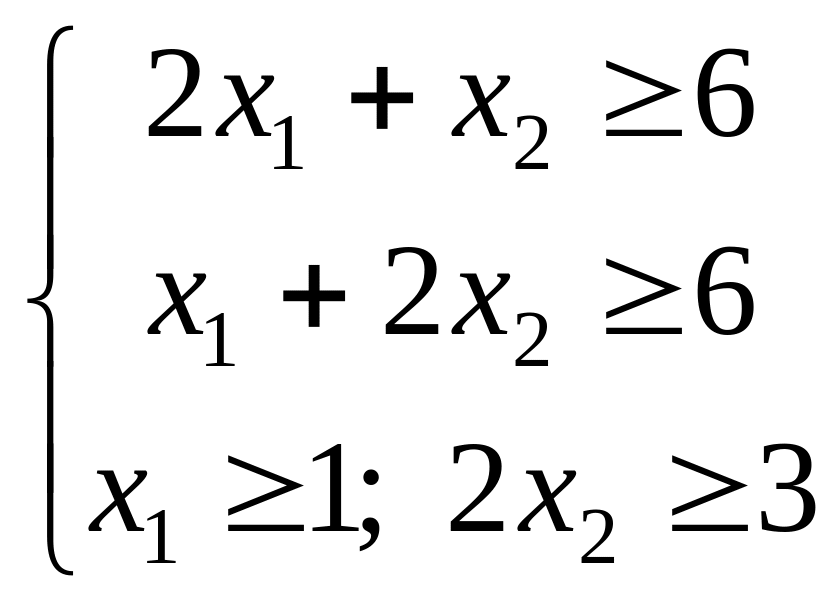
10.	11.	12.
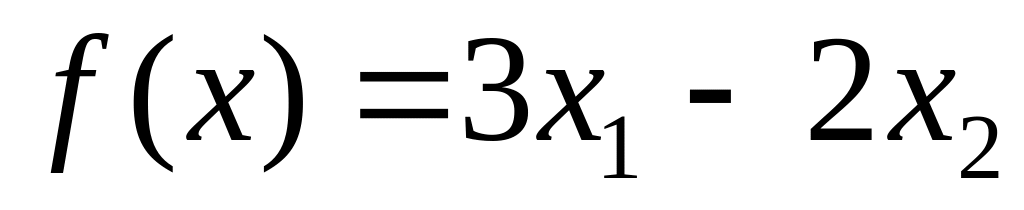
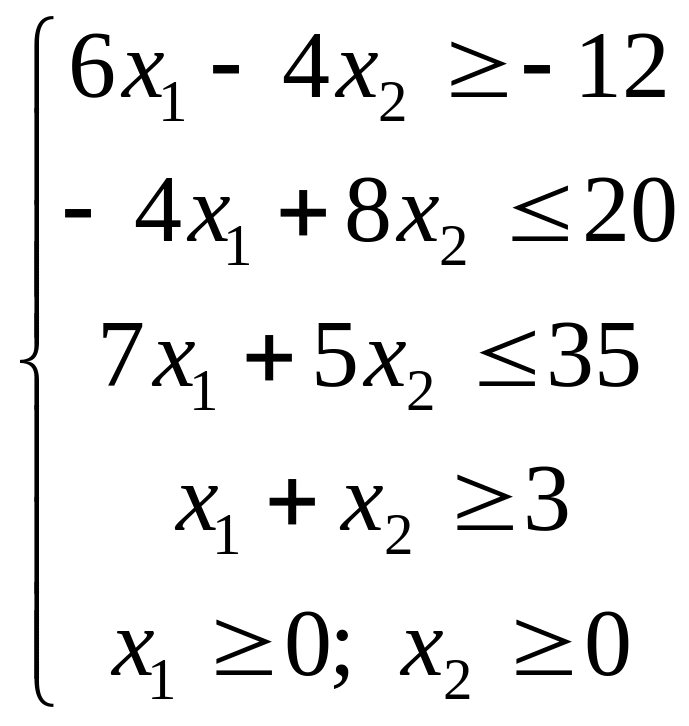
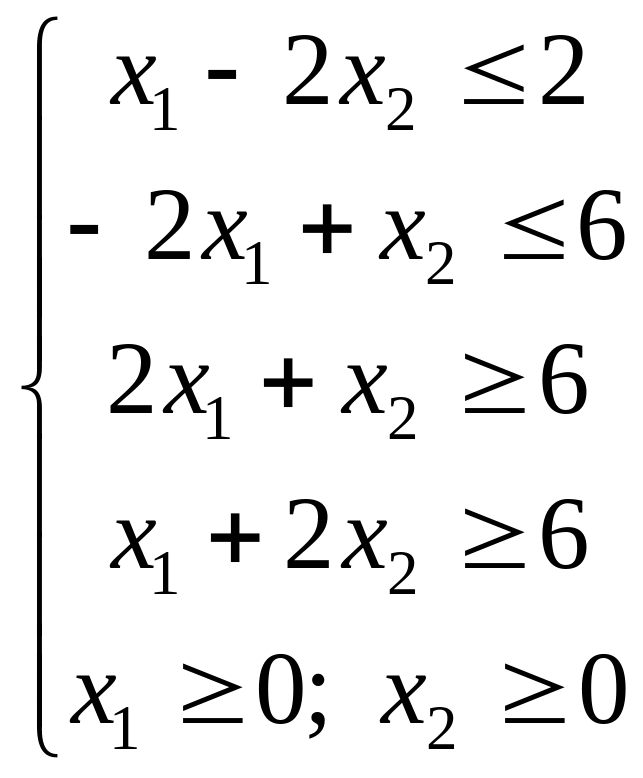
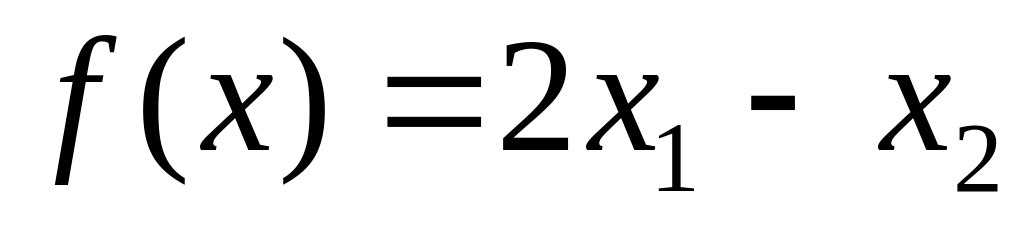
13.	14.	15. f(x) = 4x1 – 3x2 -x1 + 2x2  14 2x1 + x2  17 3x1 - x2  8 x1 + x2  4 x1  0; x2  0
16. f(x) = 2x1 + x2 x1 + x2  3 2x1 + 3x2  15 2x1 – 2,5x2  10 x1  0 0  x2  4	17.	18. f(x) = -x1 + 2x2 -x1 - 8x2  10 x1 + x2  1 x1 - 5x2  -5 3x1 + 10x2  30 x1  0; x2  0
19.	20. f(x) = x1 - 2x2 5x1 + x2  6 2x1 – 3x2  -3 2x1 + 2x2  3 x1, x2  0	21.
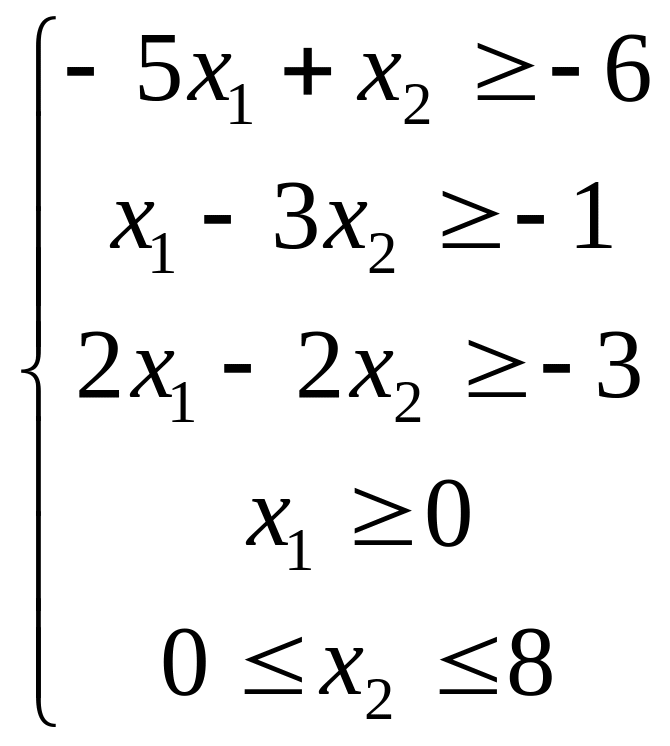
22. f(x) = -x1 + 3x2 -x1 + x2  -6 x1 + 3x2  5 x1 + x2  3 x1  0 -2  x2  4	23. f(x) = -10x1 + 2x2 2,5x1 + x2  5 4x1 + 3x2  5 -x1 + x2  -3 x1 - x2  7 0  x2  2	24. f(x) = x1 – 10x2 5x1 - x2  0,5 8x1 + x2  2 x1 + 13x2  5 x1  7 0  x2  1
25.	26. f(x) =8x1 – x2 4x1 - x2  1 -x1 + 5x2  7 x1 + x2  10 x1  0, x2  0	27. f(x) = x1 – x2 9x1 + x2  5 -x1 + 10x2  -6 x1 + 4x2  8 x1  0, x2  0

При выполнении индивидуального задангия привести номер задания, само задание, дать графическое решение и сделать по окончании выводы.