Биноминальное распределение

Пусть производится n независимых испытаний, в каждом из которых событие A может появиться, либо не появиться. Вероятность наступления события во всех испытаниях постоянна равна p (вероятность не появления q=1-p). Пусть X – число появлений события A в этих испытаниях. Найдем закон распределения величины X:

X	n	n-1	…	k	…	0
P	pn	npn-1q	…	Cnkpkqn-k	…	qn

Найдем мат.ожидание и дисперсию.

Очевидно, что общее число появлений события А складывается из чисел появлений события в отдельных испытаниях, т.е.

X1	1	0
P	p	q

, значит .

Аналогично,

, т.е. .

Пример: Проводятся 10 независимых испытаний, в каждом из которых вероятность появления события равна 0,6. Найти закон распределения, мат.ожидание и дисперсию случайной величины X – числа появления события в этих испытаниях.

Решение: n=10; p=0,6; q=0,4.

X	0	1	…	10
P	0,4n	С101 0,61 0,49	…	0,6n

• Если же в задаче количество испытаний велико, то вместо формулы Бернулли используют асимптотическую формулу Лапласа

где .

Причем, - имеются таблицы для этой функции.

• Если же в задаче количество испытаний велико, а р – мало ( 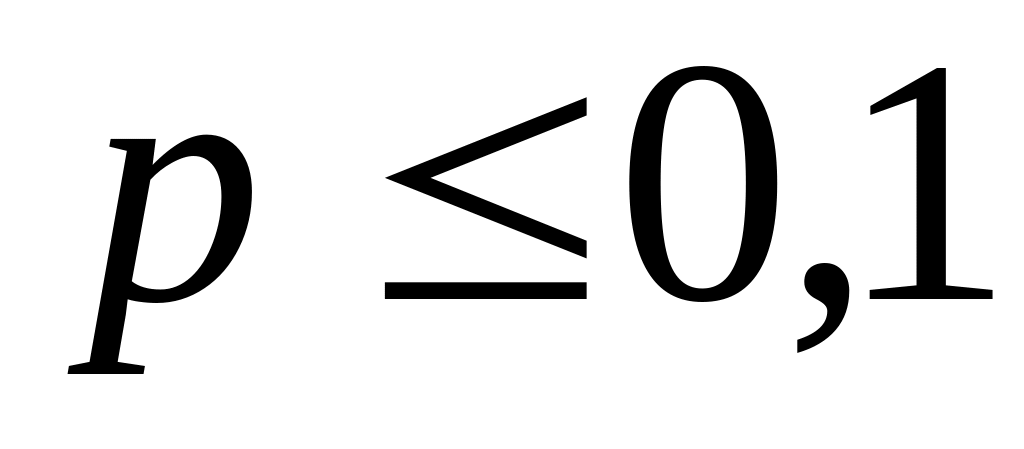), то используют асимптотическую формулу Пуассона

где . Это закон распределения Пуассона.

Пример:

Найти вероятность того, что событие A наступит ровно 80 раз в 400 испытаниях, если р=0,2.

Решение:

n=400; k=80; p=0,2; q=0,8.

По формуле Лапласа

,

По формуле Бернулли

Замечание: Если n=10; k=8; p=0,75; q=0,25, то

По формуле Лапласа ,

,

По формуле Бернулли

.

Вывод: Так как n – мало, то расхождение большое.

Пример: Завод отправил на базу 5000 доброкачественных деталей. Вероятность того, что изделие в пути повредится 0,0002. Найти вероятность того, что на базу придут 3 негодных изделия.

Решение: Если n=5000; k=3; p=0,0002, то по формуле Пуассона

где .

Значит,

Закон больших чисел

Как мы знаем, нельзя заранее предвидеть, какое из возможных событий примет случайная величина в итоге испытания. Это зависит от многих случайных причин.

Казалось бы, что поскольку о каждой случайной величине мы располагаем скромными сведениями, вряд ли можно установить закономерности поведения и суммы достаточно большого числа случайных величин.

Но оказывается, что суммарное поведение достаточно большого числа случайных величин утрачивает случайный характер и становится закономерным.

Неравенство Чебышева: (справедливо для дискретных и непрерывных случайных величин). Рассмотрим для дискретного случая.

Пусть

X	x1	x2	x3	…	xn
P	p1	p2	p3	…	pn

- вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине меньше положительного числа не меньше, чем .

Доказательство: ,

.

Найдем дисперсию

Очевидно, что все слагаемые этой суммы неотрицательные. Отбросим те слагаемые, у которых , значит сумма от этого может только уменьшиться

Но , т.е.

Значит, ч.т.д.

Теорема Чебышева:

Если попарно независимые случайные величины, причем , то для любого малого

Пояснение: Хотя отдельные независимые случайные величины могут принимать значения далекие от своих математических ожиданий – среднее арифметическое достаточно большого числа случайных величин с большей вероятностью принимает значения, близкие к постоянному числу .

Итак, среднее значение достаточно большого числа независимых случайных величин утрачивает характер случайной величины.

Теорема Бернулли ( закон больших чисел):

,

где - относительная частота, p- вероятность появления события A.

Пример: Пользуясь неравенством Чебышева, оценить вероятность того, что

, если .

Решение:

.