Случайные величины

Определение: Случайной величиной называется величина, которая в результате опыта может принимать определенное (но заранее неизвестное) значение.

Пример: 1) Число студентов на занятии по математике есть дискретная случайная величина 0,1,2,…,25 (если в группе 25 человек), но заранее неизвестно сколько их будет.

2)Скорость встречного автомобиля или ошибка взвешивания на точных весах.

В первом примере случайная величина принимает одно из значений 0,1,2,…,25 - это отдельные изолированные возможные значения.

Во втором примере, случайные величины могут принимать любое значение из промежутка (a, b).нельзя отделить одно возможное значение от другого промежутком.

Значит, целесообразно различить дискретные и непрерывные случайные величины.

Определение: Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, что возможных значений непрерывной случайной величины – бесконечно.

Дискретные случайные величины.

Случайные величины обозначаются заглавными буквами X, Y, Z.

Запись X=x означает, что случайная величина приняла значение x.

Запись P(X=x) означает вероятность того, что случайная величина X приняла значение x.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями. Его можно задать таблично, аналитически (в виде формулы) и графически.

Табличный способ (или ряд распределения)

X	x1	x2	x3	…	xn	- возможные значения
P	p1	p2	p3	…	pn	- их вероятности

Т.к. в одном испытании случайная величина принимает одно и только одно возможное значение, то события X=x₁,… X=x_n – образуют полную группу, значит, .

Пример: В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 руб. и 10 выигрышей по 1руб. Найти закон распределения случайной величины X – стоимости возможного выигрыша для владельца одного билета.

X	50	1	0
P			1- -

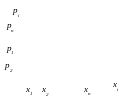
Графический ряд распределения (многоугольник или полигон распределения). В прямоугольной системе координат строятся точки и затем соединяются.

Числовые характеристики дискретной случайной величины

Закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями.

1. Математическое ожидание m(X).

Математическим ожиданием M(X) случайной величины X называется сумма произведений всех ее возможных значений на соответствующие вероятности, т.е. .

Смысл математического ожидания. Пусть произведено N независимых опытов, в каждом из которых X принимает определенное значение. Например,

x₁ появилось m₁ раз,

x₂ появилось m₂ раз,

. . .

x_n появилось m_n раз.

Ясно, что m₁+ m₂+…+ m_n=N.

Вычислим среднее арифметическое найденных случайных величин:

, но

- относительные частоты, т.е.

.

Допустим, что число испытаний достаточно велико, значит

, т.е.

,

Или

.

Значит математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины.

Пример:

1)

X	3	5	2
P	0,1	0,6	0,3

2)Найти математическое ожидание числа появлений события А в одном испытании, если вероятность появления события А равно р.

X	1	0
P	р	q

.

Прежде, чем рассматривать свойства математического ожидания, введем некоторые понятия.

Определение 1. С – постоянная дискретная случайная величина. Она принимает одно возможное значение С с вероятностью р=1.

X	С
P	1

Определение 2. СX –дискретная случайная величина, которая имеет вид и

Если

X	x1	x2	x3	…	xn
P	p1	p2	p3	…	pn

то

СX	Сx1	Сx2	Сx3	…	Сxn
P	p1	p2	p3	…	pn

Т.е. возможные значения случайной величины СХ равны Сx_i, а вероятности равны соответствующим вероятностям случайной величины Х.

Определение 3. Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина.

Определение 4. Произведение независимых случайных величин Z=XY.

Если

X	x1	x2
P	p1	p2

Y	y1	y2
P	g1	g2

то

XY	x1 y1	x2 y1	x1 y2	x2 y2	- возможные значения
P	p1 g1	p2 g1	p1 g2	p2 g2	- их вероятности

Определение5. Суммой случайных величин X и Y Z=X+Y , называют случайную величину, возможные значения которой равны суммам каждого возможного значения Х с каждым возможным значением Y. Вероятности возможных значений Z=X+Y для независимых величин X и Y равны произведениям вероятностей слагаемых, для зависимых величин – произведениям вероятности одного слагаемого на условную вероятность второго.

Если

X	x1	x2
P	p1	p2

Y	y1	y2
P	g1	g2

то

X+Y	x1 +y1	x2 +y1	x1 +y2	x2 +y2	- возможные значения
P	p11	p21	p12	p22	- их вероятности

СВОЙСТВА МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ

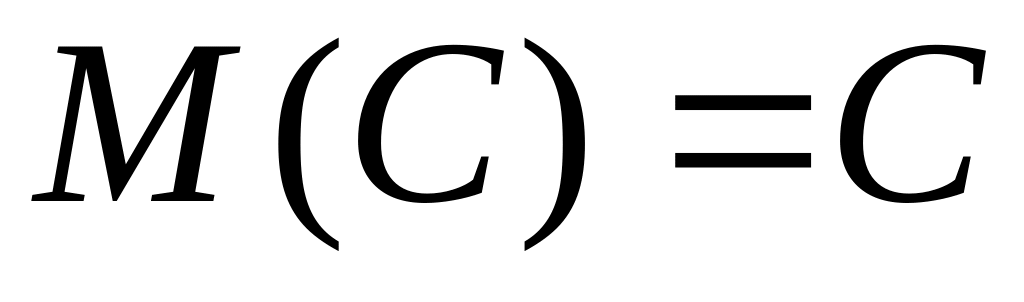1. , т.к.

Доказательство:

X	С
P	1

.

2. 

Доказательство:

Пусть

X	x1	x2	x3	…	xn
P	p1	p2	p3	…	pn

тогда

СX	Сx1	Сx2	Сx3	…	Сxn
P	p1	p2	p3	…	pn

Вычислим мат. ожидание

.

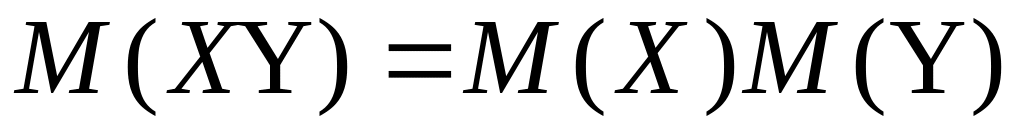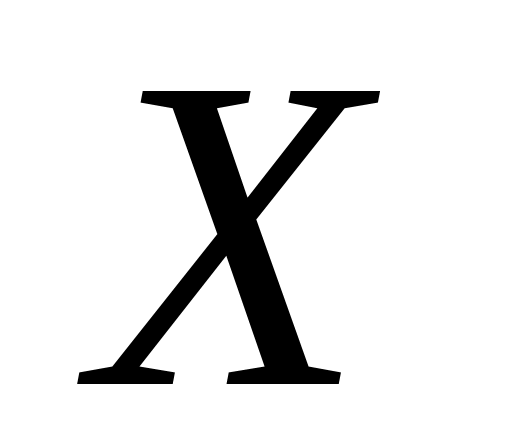3. , где и независимые случайные величины.

Доказательство:

Пусть

X	x1	x2
P	p1	p2

Y	y1	y2
P	g1	g2

тогда

XY	x1 y1	x2 y1	x1 y2	x2 y2	- возможные значения
P	p1 g1	p2 g1	p1 g2	p2 g2	- их вероятности

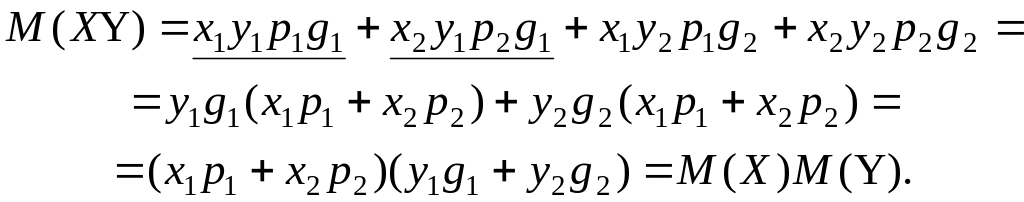
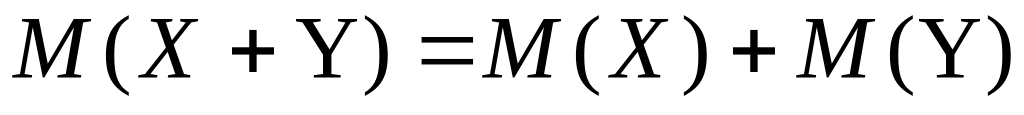4. , где и необязательно независимые случайные величины, могут быть и зависимыми.

Доказательство:

Пусть

X	x1	x2
P	p1	p2

Y	y1	y2
P	g1	g2

тогда

X+Y	x1 +y1	x2 +y1	x1 +y2	x2 +y2
P	p11	p21	p12	p22

Ясно, что

Докажем, что . Пусть событие принимает значение

x₁ +y₁ или x₁ +y₂.

Значит, вероятность - это вероятность наступления события x₁, т.е. .

Аналогично, , , .

Значит,

Следствие: .

Примеры: 1. Производится 3 выстрела с вероятностями попадания в цель ; и . Найти мат.ожидание общего числа попадания.

Решение: Пусть X₁ – число попаданий при первом выстреле,

X₂ – число попаданий при втором выстреле,

X₃ – число попаданий при третьем выстреле.

X1	1	0
P	0,4	1-0,4

X2	1	0
P	0,3	0,7

X3	1	0
P	0,6	0,4

- общее число попаданий.

попаданий.

2. Найти мат.ожидание суммы числа очков, которые могут выпасть при бросании двух игральных костей.

Решение: Пусть X₁ – число очков на первой кости,

X₂ – число очков на второй кости.

X1	1	2	3	4	5	6
P

X2	1	2	3	4	5	6
P

;

;

.