
- •2. Ток i0 силой течёт по длинному сверхпроводящему соленоиду l длиной. Найти ток I силой в соленоиде после того, как его растянули, увеличив длину на ζl величину.
- •13. Шар r радиуса находится в немагнитной среде с
- •17. Цилиндрический нерелятивистский протонный пучок r0 радиуса распространяется в вакууме в свободном пространстве. Протоны пучка
- •21. В направлении максимального излучения в вакууме на r0 расстоянии от элементарного диполя в волновой зоне излучения этого диполя известна амплитуда e0m вектора
- •22. Электрический диполь с известным и постоянным модулем pe вектора
- •36. На дифракционную решётку нормально её поверхности падает монохроматический свет с λ0 длиной волны в вакууме, равной 650 нм. За этой дифракционной решёткой находится
pe
дипольного электрического момента
вращают с известным ω
модулем
вектора ω
угловой скорости вокруг
OO′
оси, которая перпендикулярна
OO′′
оси электрического
диполя и проходит через середину прямой
линии,
22. Электрический диполь с известным и постоянным модулем pe вектора

соединяющей отрицательный и положительный заряды диполя. Найти среднюю <P> мощность излучения данного электрического диполя.
Ответ: <P> = ω4pe2/6πεε0v3, где v = 1/(εε0μμ0)1/2 - фазовая скорость электромагнитной волны в среде с ε диэлектрической проницаемостью и с μ магнитной проницаемостью;
ε0 - электрическая постоянная; μ0 - магнитная постоянная.
[6] №4.79
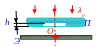
23. В опыте Ллойда монохроматическая
световая волна, исходящая из S
узкой щели, интерферирует
со световой волной, отражённой от
З
зеркала. В результате
на Э
экране образуется
система интерференционных полос. При
l
расстоянии Э
экрана и h
расстоянии З
зеркала от S
узкой щели ширина
интерференционных полос получилась,
равной Δxш.
После того, как расстояние
S узкой
щели от

З зеркала увеличили до значения h + Δh ширина Δxш′ интерференционных полос уменьшилась в η раз. Определить длину λ0 волны в вакууме монохроматической световой волны. Ответ: λ0 = 2ΔhΔxш /l(η -1).
[6] №4.81
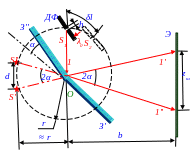
24. На ДФ диафрагму с узкой S щелью падает в вакууме монохроматическая световая волна, за которым расположено бизеркало Френеля. Угол α между З' и З'' зеркалами Френеля равен 12' , т.е.
α = 12', расстояние от линии пересечения зеркал, на которой находится O точка, до этой узкой S щели и Э экрана равны соответственно r = 10,0 см и b = 130 см. Длина волны света в вакууме монохроматической световой волны λ0 = 0,55 мкм.
Определить: а) ширину Δzш интерференционной полосы на Э экране и m число возможных интерференционных максимумов, возникающих на этом Э экране; б) сдвиг
Δz интерференционной картины на Э экране при смещении S щели по дуге окружности с центром в O точке и r = 10,0 см радиусом на длину этой дуги, равной δl = 1,0 мм; в) при какой максимальной hmax ширине S щели интерференционные полосы на Э экране будут наблюдаться достаточно отчётливо?
Ответ: а) Δzш ≈ (b + r)λ0/2rα ≈ 1,1 мм, m = (zш/Δzш) + 1 = {4brα2/[(b + r)λ0]} + 1 ≈ 9, где
zш = 2bα - ширина области, в которую попадают все отражённые лучи от З' и З'' зеркал;
б) Δz ≈ bδl/r =13 мм; в) максимальное hmax значение ширины S щели в ДФ диафрагме, до которой
можно расширять величину щели без
нарушения отчётливого изображения
интерференционных полос на Э
экране: hmax
= [1 + (r/b)]λ0/4α
≈ 43 мкм.
[6] №4.83
25. Линзу диаметром D = 5, 0 см и с фокусным расстоянием f = 25, 0 см разрезали по диаметру на две одинаковые половины, причём удалённым оказался слой толщины a = 1, 00 мм. После этого обе половины сдвинули до соприкосновения и в фокусе полученной таким образом билинзы Бийе поместили параллельно разрезу узкую щель, испускающую монохроматический свет в вакууме с λ0 = 0, 64 мкм длиной волны. За билинзой Бийе расположили экран на расстоянии
b = 50, 0 см от неё. Определить: а) ширину Δzш интерференционной полосы на экране и число
N
возможных максимумов;  б)
ширину щели hmax,
при которой полосы на экране будут
наблюдаться ещё достаточно отчётливо.
б)
ширину щели hmax,
при которой полосы на экране будут
наблюдаться ещё достаточно отчётливо.
Ответ: а) ширина интерференционных полос на Э экране Δzш ≈ λ0 f/a ≈ 0, 16 мм;
число возможных интерференционных
максимумов на Э
экране m
= (zш/Δzш)
+ 1= (ba2
/λ0
f
2)+
1 ≈
13;
б) максимальное
значение ширины щели
при которой интерференционные
полосы будут различимы согласно
критерию Релея
hmax
=
λ0
f 2/2ba
= 40 мкм.

[6] №4.88
26. На поверхности С
стекла находится П
плёнка воды. На неё падает монохроматическая
плоская световая волна с λ0
длиной волны в вакууме
под υ углом
к нормали. Найти dz/dt
скорость, с которой
уменьшается z
толщина плёнки из-за
её испарения, если при отражении
монохроматического света в фиксированном

м
где n
- показатель
преломления воды.![]()
[6] №4.95
27. Монохроматическая плоская световая волна в вакууме с длиной λ0 = 0, 55 мкм волны падает нормально на поверхность стеклянного К клина. Расстояние Δy между интерференционными максимумами, которые наблюдают в отражённом свете на поверхности этого
К клина, равно 0,
21 мм. Найти малый θ
угол между
гранями стеклянного
К клина.
Ответ: θ
= λ0/2nΔy
≈ 3',
где n
= 1, 50
- показатель преломления
стекла.

[6] №4.95
28. Плоская световая волна в вакууме с набором монохроматических компонент в некотором конечном интервале длин (λ0, λ0 + Δλ0 ) волн падает нормально на поверхность стеклянного К клина.
Расстояние Δy между интерференционными максимумами, которые наблюдают в отражённом
свете на поверхности этого К
клина, равно 0,
21 мм.
Найти степень монохроматичности
света, равное Δλ0/λ0,
если исчезновение интерференционных
полос наблюдается на l
≈
1,
5 см от вершины клина.
Ответ: Δλ0/λ0
≈
Δy
/l ≈
0.
014.

[6] №4.98
29. В схеме получения в вакууме интерференционных светлых колец Ньютона равной толщины на выпуклой поверхности стеклянной Л линзы имеется сошлифованный плоский участок
r0 = 3 мм радиуса, которым она соприкасается с верхней поверхностью Пл.2 прозрачной
пластины. Плоско - выпуклая Л
линза имеет R
= 150 см радиус кривизны. Найти rm
радиус третьего интерференционного
максимума, т.е. третьего светлого кольца,
если монохроматический параллельный
пучок света, падающий на Пл.1
прозрачную пластину, имеет λ0
длину волны в вакууме, равную
655 нм.
Ответ:
m
= 5 -
номер третьего
светлого кольца.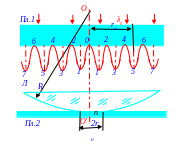
![]() где
где
[6] №4.104
30. В интерферометре Майкельсона использовалась желтая линия спектра излучения натрия, состоящая из двух близких по величине световых волн длиной λ1, λ2 в вакууме, где λ2 > λ1. Объяснить, почему при перемещении Пд. З. подвижного зеркала интерференционная картина на Э экране периодически исчезала? Найти величину Δl перемещения Пд. З. подвижного зеркала между двумя последовательными появлениями на Э экране чёткой интерференционной картины.
Ответ: перемещение Пд. З. подвижного зеркала на расстояние Δl ≈ mλ/2, где λ ≈ λ1 ≈ λ2, от предыдущего положения этого Пд. З. подвижного зеркала наблюдения, когда появилась чёткая интерференционной картина на Э экране, приводит к появлению последующей чёткой интерференционной картины, если выполняется следующее соотношение: (m+1)λ1 = mλ2,т.е. на дополнительной 2Δl длине оптического хода лучей в интерферометре Майкельсона будет укладываться целое m число λ2 длин волн и m+1 число λ1 длин волн, тогда к экрану эти λ1, λ2 длины волн
λ1
длин волн, тогда
к экрану эти λ1,
λ2
длины волн придут в одной
фазе, вследствие чего на Э
экране возникнет чёткая
интерференционная картина. С учётом
соотношения λ2
≈ λ1
+ Δλ ≈
λ+ Δλ выражение (m+1)λ1
=
mλ2
принимает следующий
вид: (m+1)λ
=m(λ+
Δλ) ↔ m
= λ/Δλ, подстановка
которого в выражение Δl
≈
mλ/2, приводит к ответу
Δl
≈
λ2/2Δλ,
где Δλ = λ2
-
λ1.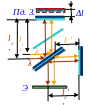

[6] №4.112
31. Между S точечным источником света и Э экраном поместили Д диафрагму с круглым отверстием, rm радиус которого можно менять. Задано a расстояние от S точечного источника света до Д диафрагмы и b расстояние от Д диафрагмы до Э экрана. Определить λ0 длину волны в вакууме,
если максимум освещенности в O
центре дифракционной картины на
Э экране
наблюдается при rm
радиусе круглого
отверстия, а следующий максимум
освещенности в O
центре дифракционной картины на Э
экране
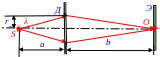
наблюдается при увеличении радиуса круглого отверстия до величины rm+2.
Ответ:
![]()
[6] №4.117
32. Монохроматическая
плоская световая волна с λ0
длиной волны в
вакууме падает нормально
на достаточно большую стеклянную П
пластину, на обратной
стороне которой сделана круглая выемка,
глубину h
которой можно менять.
Из O
точки
наблюдения выемка открывает первые полторы зоны Френеля. Определить h1 глубину выемки, при которой будет максимум освещенности в O центре дифракционной картины на
Э экране, определить h2 глубину выемки, при которой будет минимум освещенности в O центре дифракционной картины на Э экране, а также определить h3 глубину выемки, при которой освещенность в O центре дифракционной картины на Э экране будет равной освещенности падающего света.
О

где n = 1, 50 - показатель преломления стекла; m = 0, 1, 2, …
[6] №4.133
33. Монохроматическая
плоская световая волна с λ0
длиной волны в
вакууме падает нормально
на длинную по OX
оси и узкую d
шириной по OZ
оси щель, сделанной
в достаточно большой Д
диафрагме. Определить
при дифракции Фраунгофера зависимость
Iυ
интенсивности световой волны на
Э экране
от υ угла к
главной оптической оси Л
линзы, а также определить υmin
угловое положение дифракционных
минимумов.
где k
= 1,
2,
3,
…, …; Id
- интенсивность световой волны после
прохождения параллельным пучком одной
щели d
шириной в центре Э
экрана, т.е. на OX
оси.
Ответ: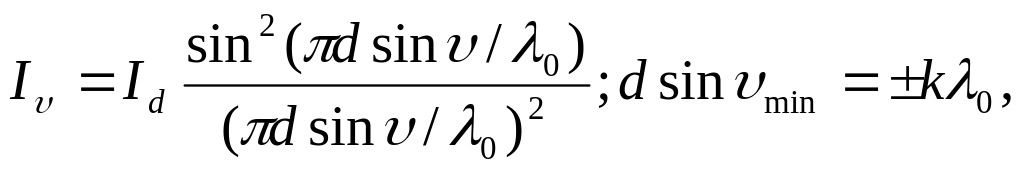
[6] №4.138
34. Монохроматическая плоская
световая волна с длиной λ0
волны в вакууме падает нормально
на три длинных по OX
оси и одинаково узких d
шириной по OZ
оси щели, сделанных в достаточно
большой Д
диафрагме. Изобразить при дифракции
Фраунгофера две примерные графические
зависимости Iυ
интенсивности световой волны на
Э экране от υ
угла к главной оптической оси Л
линзы для случаев, когда отношение h
периода решётки к
одинаковой d
ширине щелей равно двум
и когда равно трём.
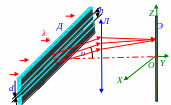
Ответ: на перпендикулярах, направленных от каждой из трёх щелей к Э экрану, т.е. под υ0 = 0 углом, будут находиться центральные дифракционные максимумы, расстояния между которыми в случае h/d = 2 будет равно 2d, а в случае h/d = 3 будет равно 3d; угловая ширина δυ этих центральных дифракционных максимумов, которые определяются δυ = λ0/d выражением, в случае h/d = 2 и в случае h/d = 3 одинакова, поскольку d ширин по OZ оси щели постоянна.
[6] №4.142
35. Монохроматическая плоская световая волна с длиной λ0 = 530 нм волны в вакууме падает в 1 - ом случае нормально, а во 2 - ом случае под υ углом к n нормали ДР дифракционной решётки,
период которой равен h
= 1, 5
мкм. Найти φ1max,
φ2max
углы относительно
n
нормали к ДР
дифракционной решётке,
под которыми образуются на
Э
экране дифракционные
максимумы наибольшего порядка в 1
- ом и во 2
- ом случаях.
Ответ: 1)
sinφ1max
= ± m1maxh/λ0,
где m1max
< h/λ0
-
наибольший порядок
дифракционного максимума, который
определяют округлением до ближайшего
целого числа, меньшего отношения h/λ0,
поэтому m1max
= 2
и φ1max
= 45º,
φ1max
= - 45º,
т.е. дифракционные максимумы наибольшего
2 -го
порядка в 1
- ом случае расположены
симметрично

относительно центрального 0 -го порядка дифракционного максимума, находящегося на OY оси;
2)
![]() ,
где m2max
< h/λ0
(1+ sinυ)
- наибольший порядок
дифракционного максимума, который
определяют округлением до ближайшего
целого числа, меньшего отношения h/λ0
(1+ sinυ),
поэтому m2max
= 5 и φ2max
= 64º, φ2max
= - 64º, т.е.
дифракционные максимумы наибольшего
5 -го
порядка во 2
- ом случае расположены
симметрично относительно OY
оси, но не симметрично
относительно центрального 0
-го порядка
дифракционного максимума, находящегося
под φ0
= - υ
= - 60º углом к OY
оси.
,
где m2max
< h/λ0
(1+ sinυ)
- наибольший порядок
дифракционного максимума, который
определяют округлением до ближайшего
целого числа, меньшего отношения h/λ0
(1+ sinυ),
поэтому m2max
= 5 и φ2max
= 64º, φ2max
= - 64º, т.е.
дифракционные максимумы наибольшего
5 -го
порядка во 2
- ом случае расположены
симметрично относительно OY
оси, но не симметрично
относительно центрального 0
-го порядка
дифракционного максимума, находящегося
под φ0
= - υ
= - 60º углом к OY
оси.
[7] №31.28
