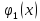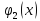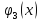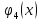Задание №1

Цены двух видов товаров равны соответственно P₁ = 27 и P₂ = 21 денежных единиц. Определить, при каких количествах x и y продаж этих товаров прибыль будет максимальной, если функция издержек имеет вид

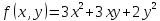
Решение

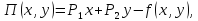
где П(х, у) — прибыль

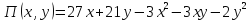
Для начала найдём стационарную точку (подозрительную на экстремум). Для этого приравняем первые частные производные функции прибыли к 0 и решим полученную систему уравнений.

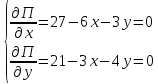
Умножив второе уравнение на 2 и вычтя из него первое, получим

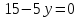
Отсюда y = 3. Подставив полученное значение во второе уравнение системы, получим, что у = 3. Таким образом, точка (3; 3) является подозрительной на экстремум. Чтобы проверить наличие и характер экстремума, составим матрицу вторых производных W функции прибыли в стационарной точке и найдём её определитель.

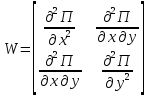
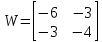
det W = -6*(-4) – (-3)*(-3) = 15 > 0

Определитель матрицы W положительный, значит, в стационарной точке экстремум. 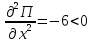, значит, в этой точке максимум.

Значение функции прибыли: П(3, 3) = 27*3+21*3–3*3² –3*3*3–2*3²=72 ден.ед.

Ответ: 3 единицы первого товара и 3 единицы второго товара. Максимальная прибыль составит 72 ден.ед.

Задание №2

Предположим, что для изготовления продукции Р1 и Р2 требуется использование трёх видов ресурсов R1, R2, R3. Количество ресурсов и нормы их расхода на изготовление единицы каждого вида продукции известны и задаются в таблице

Виды ресурсов	Количество ресурсов	Р1	Р2
R1	65	2.5−0.015х1	4.5−0.03х2
R2	70	3	1
R3	100	2	3

Прибыль, получаемая предприятием от реализации единицы продукции Р1 и Р2, составляет соответственно 4−0.15х₁ и 3−0.1х₂ Требуется составить такой план выпуска продукции видов Р1 и Р2, при котором прибыль предприятия от реализации продукции оказалась бы максимальной.

Решение

Запишем целевую функцию прибыли z и систему ограничений по ресурсам.

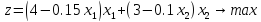
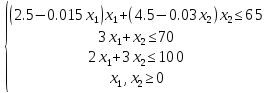
Для начала найдём экстремальную точку. Если она принадлежит области допустимых решений, заданной ограничениями, необходимо будет проверить характер этой точки и завершить решение. Для этого частные производные приравняем нулю и решим полученную систему.

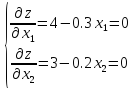
Отсюда 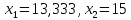, z=49,167.

Проверим на выполнение ограничений.

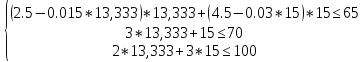
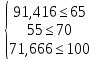
Первое ограничение нарушено, экстремальная точка выходит за область допустимых решений. Решаем графическим способом.

Построим графики ограничений и линии уровня целевой функции z. Они представлены на рисунке 1. Областью допустимых решений задачи является фигура OABC.

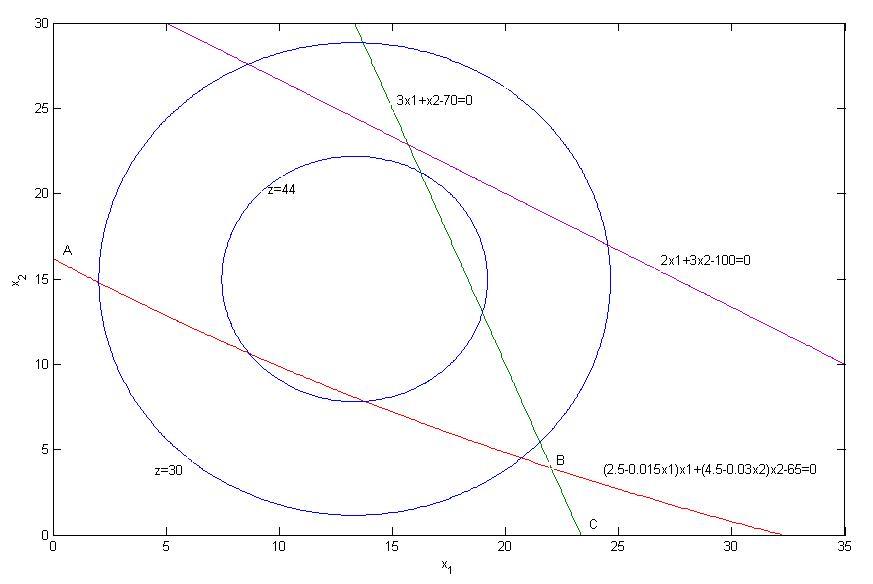
Рисунок 1 — Область допустимых решений задачи

Очевидно, что при увеличении значения целевой функции крайняя точка, когда линия уровня функции ещё будет касаться области допустимых решений, будет лежать на линии 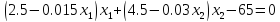(первое ограничение). Соответственно, градиенты целевой функции и первого ограничения в этой точке будут лежать на одной прямой, то есть, их координаты будут пропорциональны. Запишем координаты градиентов и составим систему уравнений.

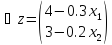
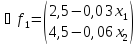
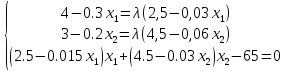
Преобразуем первое уравнение.

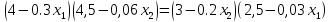
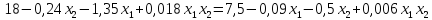
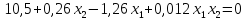
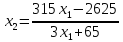
Система примет вид

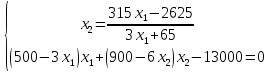
Теперь подставим первое уравнение во второе.

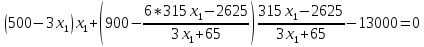
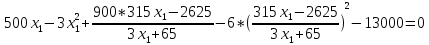
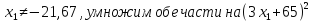
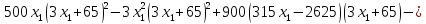
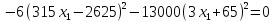
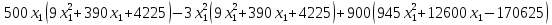
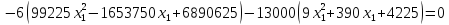
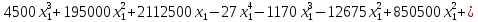
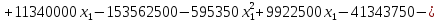
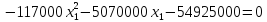
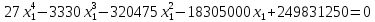
Для решения данного уравнения воспользуемся методом Ньютона. По графику на рис. 1 видно, что корень принадлежит интервалу [10; 14].

Для того, чтобы решить уравнение методом Ньютона, необходимо проверить несколько условий:

1. Функция f(x) определена и дважды дифференцируема на данном интервале.

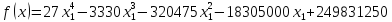
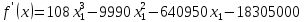
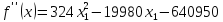
Условие выполняется.

2. Интервалу принадлежит только один простой корень уравнения.

Условие выполняется.

3. Производные 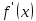и 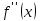на интервале сохраняют знак,

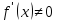
Если знаки в начале и конце интервала будут совпадать, значит, на интервале знак сохраняется.

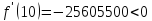
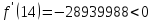
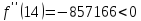
Производные сохраняют знак на интервале.

Возьмём начальное приближение 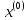так, чтобы выполнялось условие

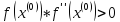Например, 14 ()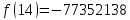

Вычисления будем производить по формуле:

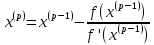
Зададим точность 0,0001.

В итоге получилось

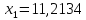
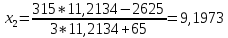
Проверим решение на соответствие ограничениям (знак равенства в первом, потому что оптимальная точка лежит на этой линии, как было установлено)

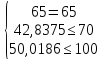
В данной точке значение целевой функции

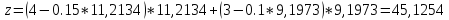
Ответ:

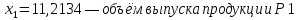
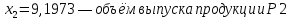
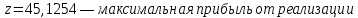
Задание №3

Известно, что, если k-му предприятию выделить 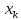единиц ресурсов, то количество произведённой продукции будет равно 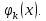Требуется распределить А единиц ресурсов между всеми предприятиями так, чтобы выпуск продукции был максимальным.

x ед. ресурсов
1	2	4	3	3
2	4	4	5	4
3	8	6	7	7
4	8	8	9	10
5	9	10	10	10
6	10	11	11	12

Решение:

Будем решать задачу методом динамического программирования. Обозначим 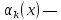количество ресурсов, которое достанется k-му предприятию, 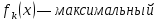суммарный выпуск продукции на предприятиях c 1 по k, находится по формуле

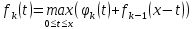
Общий ход решения будет представлен в таблице 1.

Сначала возьмём только первое предприятие. ,

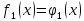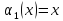
Затем рассмотрим вместе 1 и 2 предприятия.

Распределяем один ресурс:

1→1 предприятие, 0→2 предприятие; выпуск = 2

0→1 предприятие, 1→2 предприятие; выпуск = 4 — максимальное значение

Распределяем два ресурса:

2→1 предприятие, 0→2 предприятие; выпуск = 4

1→1 предприятие, 1→2 предприятие; выпуск = 6 — максимальное значение

0→1 предприятие, 2→2 предприятие; выпуск = 4

Распределяем три ресурса:

3→1 предприятие, 0→2 предприятие; выпуск = 8 — максимальное значение

2→1 предприятие, 1→2 предприятие; выпуск = 8 — максимальное значение

1→1 предприятие, 2→2 предприятие; выпуск = 6

0→1 предприятие, 3→2 предприятие; выпуск = 6

2