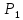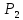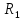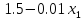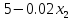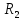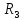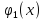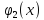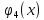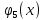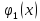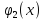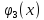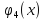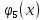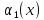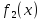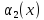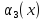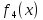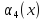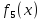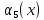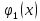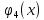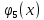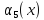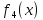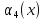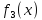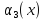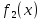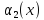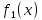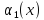Математическое моделирование / РГР по Матмод Вариант 5
.docxМинистерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Новосибирский государственный технический университет»
Факультет бизнеса
Кафедра экономической информатики
Расчетно-графическая работа
по дисциплине «Математическое моделирование»
Вариант №5
Выполнила:
Студентка группы ФБИ-22
Преподаватель:
Соболева О.Н.
Новосибирск 2015
Задание №1
Цены
двух видов товаров равны соответственно
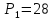и
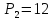денежных единиц. Определить, при каких
количествах x
и y
продаж этих товаров прибыль будет
максимальной, если функция издержек
имеет вид
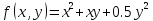
Решение:
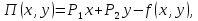
где
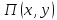– прибыль
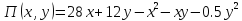
Для начала найдём стационарную точку (подозрительную на экстремум). Для этого приравняем первые частные производные функции прибыли к 0 и решим полученную систему уравнений.
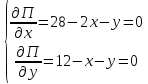
Из первого уравнения вычтем второе уравнение, получим
Отсюда
.
Подставив полученное значение в первое
уравнение системы,
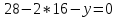
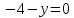
получим,
что
.
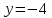Таким образом, точка (16;-4) является
подозрительной на экстремум. Чтобы
проверить наличие и характер экстремума,
составим матрицу вторых производных W
функции прибыли в стационарной точке
и найдём её определитель.
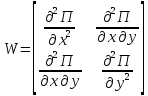
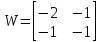
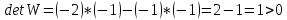
Определитель
матрицы W
положительный, значит, в стационарной
точке экстремум.
,
значит, в этой точке максимум.
Значение функции прибыли:
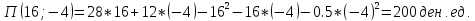
Решим данную задачу с помощью MatLab.
На рисунке 1 представлена функция для целевой функции.
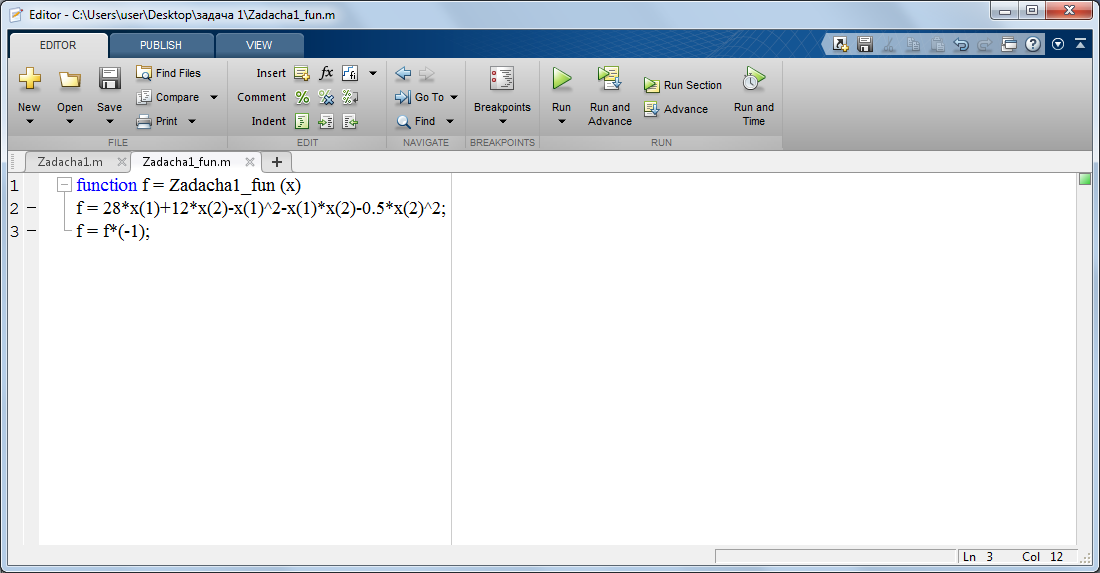
Рисунок 1 – Функция Zadacha1_fun
На рисунке2 представлен текст головной программы.
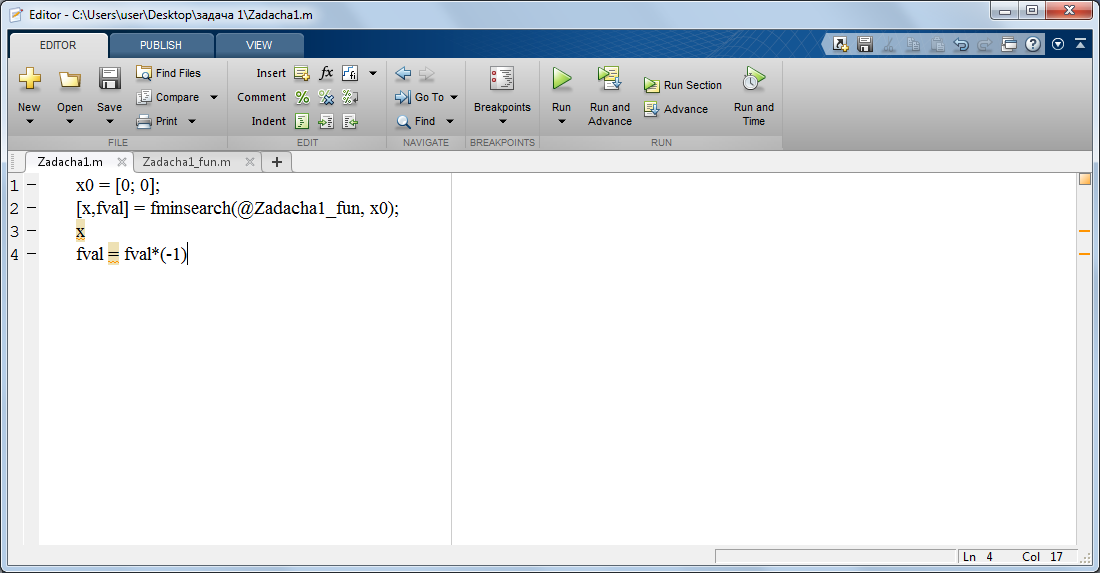
Рисунок 2 – Головная программа
На рисунке 3 представлен результат выполнения головной программы.
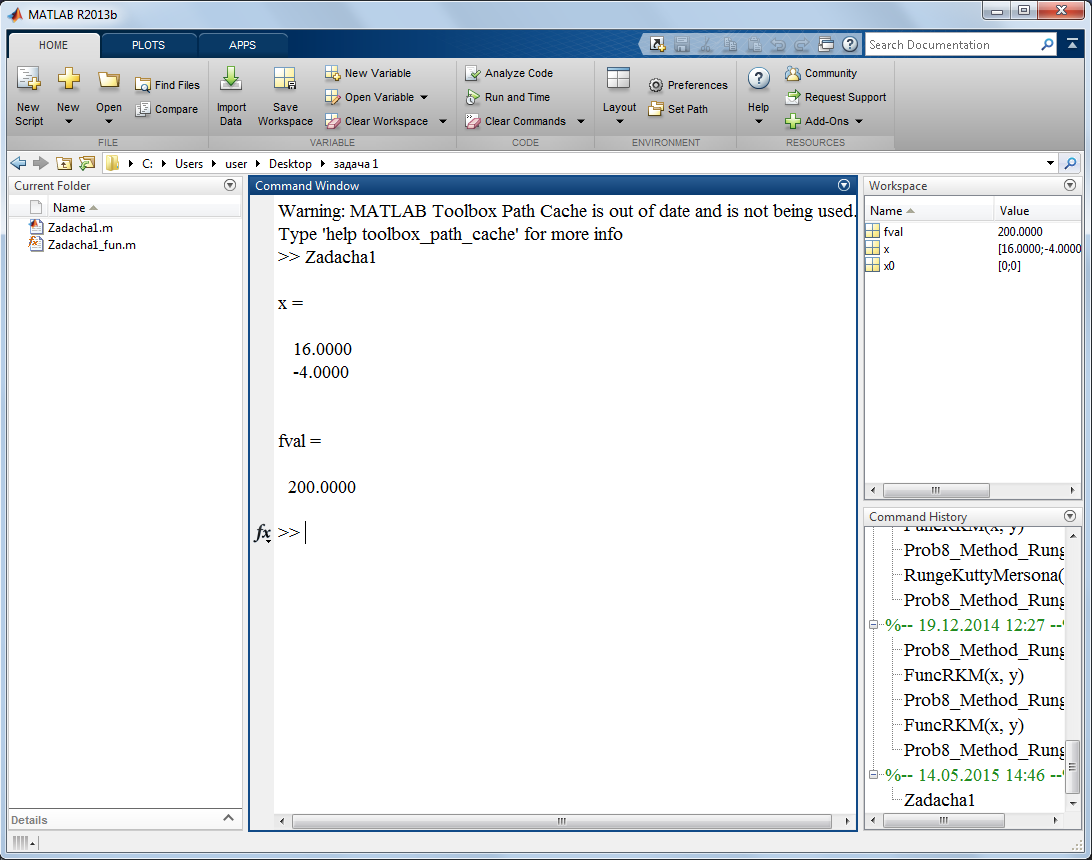
Рисунок 3 – Результат
Ответ: 16 единиц первого товара и -4 единицы второго товара. Максимальная прибыль составит 200 ден.ед.
Задание №2
Предположим,
что для изготовления продукции
и
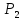требуется использование трёх видов
ресурсов
.
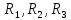Количество ресурсов и нормы их расхода
на изготовление единицы каждого вида
продукции известны и задаются в таблице
1.
Таблица 1 – Данные задания №2
|
Виды ресурсов |
Количество ресурсов |
|
|
|
|
90 |
|
|
|
|
70 |
3 |
1 |
|
|
100 |
2 |
3 |
Прибыль,
получаемая предприятием от реализации
единицы продукци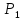и
и
,
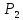составляет соответственно
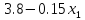и
.
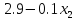Требуется составить такой план выпуска
продукции видов
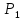и
,
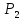при котором прибыль предприятия от
реализации продукции оказалась бы
максимальной.
Решение:
Запишем целевую функцию прибыли z и систему ограничений по ресурсам.
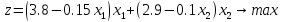
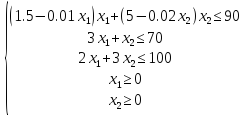
Для начала найдём экстремальную точку. Если она принадлежит области допустимых решений, заданной ограничениями, необходимо будет проверить характер этой точки и завершить решение. Для этого частные производные приравняем нулю и решим полученную систему.
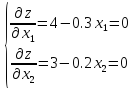
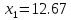
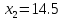
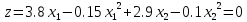
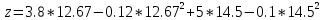
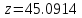
Проверим на выполнение ограничений.
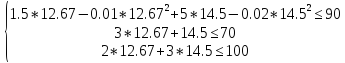
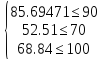
Ни одно ограничение не выходит за область ограничения.
Чтобы проверить наличие и характер экстремума, составим матрицу вторых производных W функции прибыли в стационарной точке и найдём её определитель.
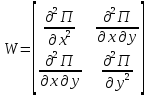
W отрицательно-определенная матрица, следовательно вогнутая функция.
Точка (12.67;14.5) точка максимума.
Задание №3
Известно,
что если k-ому
предприятию выделить
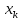единиц
ресурсов, то количество произведенной
продукции будет равно
.
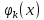Требуется распределить А единиц ресурсов
между всеми предприятиями так, чтобы
выпуск продукции был максимальным.
Обозначим
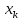количество ресурсов, которое нужно
выделить k-ому
предприятию.
Таблица 2 – Данные задания №3
|
X ед. ресурсов |
|
|
|
|
|
|
1 |
4 |
5 |
6 |
4 |
3 |
|
2 |
5 |
4 |
3 |
5 |
4 |
|
3 |
6 |
6 |
8 |
7 |
8 |
|
4 |
7 |
8 |
9 |
9 |
8 |
|
5 |
9 |
9 |
9 |
10 |
10 |
Решение:
Будем решать задачу методом динамического программирования. Обозначим
– количество
ресурсов, которое достанется k-му
предприятию,
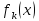– максимальный
суммарный выпуск продукции на предприятиях
c
1 по k,
находится по формуле:
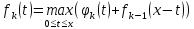
Общий ход решения будет представлен в таблице 3.
Сначала возьмём только первое предприятие.
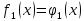
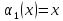
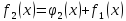
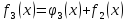
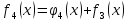
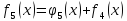
Таблица 4 – Прямой ход
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
4 |
5 |
6 |
4 |
3 |
4 |
1 |
5 |
1 |
6 |
1 |
6 |
0 |
6 |
0 |
|
2 |
5 |
4 |
3 |
5 |
4 |
5 |
2 |
5+4 9 |
1 |
6+5 11 |
1 |
10 |
1 |
3+6 9 |
1 |
|
3 |
6 |
6 |
8 |
7 |
8 |
6 |
3 |
5+5 10 |
1 |
6+9 15 |
1 |
4+10 14 |
1 |
3+10 13 |
1 |
|
4 |
7 |
8 |
9 |
9 |
8 |
7 |
4 |
6+5 11 |
1 |
6+10 16 |
1 |
4+15 19 |
1 |
3+14 17 |
1 |
|
5 |
9 |
9 |
9 |
10 |
10 |
9 |
5 |
7+5 4+8 12 |
1,4 |
8+9 6+17 17 |
1,3 |
4+16 20 |
1,2 |
3+19 22 |
1 |
Максимальный выпуск продукции = 3 + 4 + 6 + 5 + 4 = 22.
Пятому предприятию – 1 единица ресурса, выпуск = 3;
Четвертому предприятию – 1 единица ресурса, выпуск = 4;
Третьему предприятию – 1 единица ресурса, выпуск = 6;
Второму предприятию – 1 единица ресурса, выпуск = 5;
Первому предприятию – 1 единица ресурса, выпуск = 4.
Таблица 5 – обратный ход
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
4 |
5 |
6 |
4 |
3 |
3 |
1 |
4 |
1 |
6 |
1 |
6 |
0 |
6 |
0 |
|
2 |
5 |
4 |
3 |
5 |
4 |
4 |
2 |
4+3 7 |
1 |
6+4 10 |
1 |
5+6 11 |
1 |
11 |
0 |
|
3 |
6 |
6 |
8 |
7 |
8 |
8 |
3 |
5+3 4+4 8 |
1,2,3 |
6+7 13 |
1 |
5+10 15 |
1 |
4+11 15 |
0,1 |
|
4 |
7 |
8 |
9 |
9 |
8 |
8 |
4 |
4+8 12 |
1 |
6+8 14 |
1 |
5+13 18 |
1 |
4+15 19 |
1 |
|
5 |
9 |
9 |
9 |
10 |
10 |
10 |
5 |
5+8 13 |
2 |
6+12 18 |
1 |
5+14 19 |
1 |
4+18 22 |
1 |
Максимальный выпуск продукции = 4 + 5 + 6 + 4 + 3 = 22.
Первому предприятию – 1 единица ресурса, выпуск = 4;
Второму предприятию – 1 единица ресурса, выпуск = 5;
Третьему предприятию – 1 единица ресурса, выпуск = 6;
Четвертому предприятию – 1 единица ресурса, выпуск = 4;
Пятому предприятию – 1 единица ресурса, выпуск = 3.