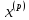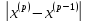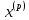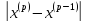Численные методы / РГР ЧМ 16 вариант
.docxМинистерство образования и науки Российской Федерации
Федеральное агентство по образованию
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Факультет бизнеса
Кафедра экономической информатики

Расчетно-графическая работа
по дисциплине «Численные методы»
Вариант 16
Выполнила:
Факультет бизнеса
Группа: ФБИ-22
Преподаватель: проф. Соболева О.Н.
Новосибирск
2014
Задание №1
Запишите порядок выполняемых вами операций, оцените погрешности их результатов, вычислите и запишите искомое значение. Определите число верных знаков.
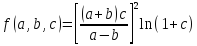
a=0,2456±0,0005;b=0,20078±0,00003;c=0,008±0,00013.
Решение
Приближенные значения исходных данных:
a=0,2456; b=0,20078; c=0,008.
Абсолютные погрешности исходных данных:
∆a=0,0005; ∆b=0,00003; ∆c=0,00013.
Относительные погрешности исходных данных:
δa=∆a/a=0,0005/0,02456=0,00203;
δb=∆b/b=0,00003/0,20078=0,00015;
δc=∆c/c=0,00013/0,008=0,01625.
Порядоквыполняемыхопераций:
-
a+b=0,44638; ∆(a+b)=∆a+∆b=0,00053; δ(a+b)=∆(a+b)/(a+b)=0,00119.
-
(a+b)*c=0,00357;∆((a+b)*c)=|a+b|*∆c+|c|*∆(a+b)=0,000058+0,0000042=
=0,000062; δ((a+b)*c)= ∆((a+b)*c)/ (a+b)*c=0,01744.
-
a-b=0,04482; ∆(a-b)=∆a+∆b=0,00053; δ(a-b)=∆(a-b)/(a-b)=0,011825.
-
(a+b)*с/(a-b)=0,07967; ∆ ((a+b)*с/(a-b))= ((a-b)*∆((a+b)*c)+(a+b)*с*
*∆(a-b))/ (a-b)^2=0,00233; δ(( a+b)*с/(a-b))= δ((a+b)*c)+ δ(a-b)= =0,01744+0,011825=0,02926.
-
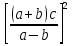 =0,006348;
∆(
=0,006348;
∆(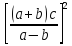 )=2*
)=2*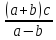 *∆
((a+b)*с/(a-b))=0,000372;
*∆
((a+b)*с/(a-b))=0,000372;
δ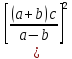 )=2*δ((
a+b)*с/(a-b))=0,058525.
)=2*δ((
a+b)*с/(a-b))=0,058525.
-
1+с=1,008; ∆(1+с)=∆с=0,00013; δ(1+с)=∆(1+с)/(1+с)=0,000129.
-
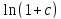 =0,00797;
∆f(x)~f’(x)∆x;∆
=0,00797;
∆f(x)~f’(x)∆x;∆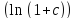 =ln’(1+с)*
∆(1+с)=(1/(1+с))* ∆(1+с)=0,99206*0,00013=0,0000128; δ(
=ln’(1+с)*
∆(1+с)=(1/(1+с))* ∆(1+с)=0,99206*0,00013=0,0000128; δ(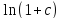 )=
∆
)=
∆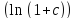 /
/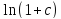 =0,01618.
=0,01618. -
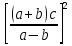 *
*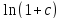 =0,00005059;
∆(
=0,00005059;
∆(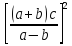 *
*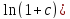 =
|
=
|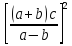 |*∆
|*∆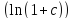 +
|
+
|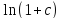 |*
∆(
|*
∆(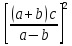 )=0,006348*0,0000128+0,00797*0,000372=0,000003046;
)=0,006348*0,0000128+0,00797*0,000372=0,000003046;
δ
(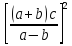 *
*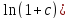 =
(∆(
=
(∆(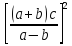 *
*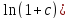 )/
)/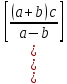 *
*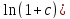 =0,060211.
=0,060211.
Определение числа верных знаков:
F=0,00005059;
∆F=0,000003046=0,3*10-5;
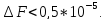
9:
10-8 0,5*10-8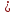 0,3*10-5
0,3*10-5
5:
10-7 0,5*10-7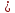 0,3*10-5
0,3*10-5
0:
10-6 0,5*10-6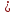 0,3*10-5
0,3*10-5
5:
10-5 0,5*10-5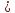 0,3*10-5
0,3*10-5
Ответ: Число верных знаков m=1. F=0,00005059.
Задание №2
Выяснить погрешность задания исходных данных, необходимую для получения результата с m верными значащими цифрами.
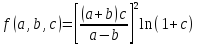
a=0,
2456; b=0,20078; c=0,008,
Решение
Из
предыдущего задания:
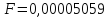 ,
верные знаки: 5,0,5,9.
,
верные знаки: 5,0,5,9.
Тогда
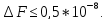
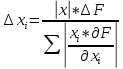
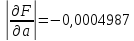 ;
;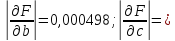 0,018944.
0,018944.
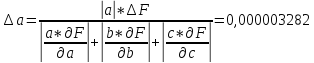 ;
;
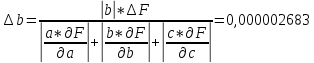 ;
;
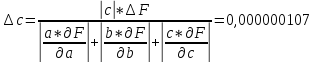 ;
;
Ответ: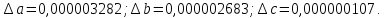
Задание №3
Решить
СЛАУ методом Гаусса и с точностью до
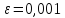 методом
простой итерации.
методом
простой итерации.
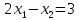 ;
;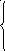
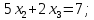
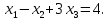
Решение методом Гаусса.
Запишем систему в виде расширенной матрицы и приведем матрицу к треугольному виду с помощью элементарных преобразований:

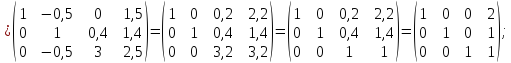
Получена эквивалентная система:
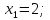
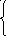
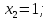
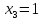 .
.
Ответ: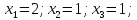
Решение методом простой итерации
Матрица с диагональным преобладанием.
Выразим
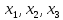 из первого, втрого и третьего уравнений
соответственно:
из первого, втрого и третьего уравнений
соответственно:
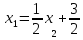 ;
;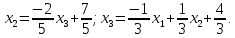
Тогда матрица примет вид:
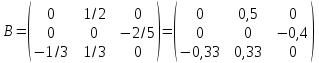 ;
;
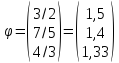
Норма
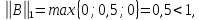 значит,
матрица сходится.
значит,
матрица сходится.
Зададим начальное приближение:
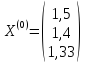 ;
;
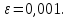
Выполним
расчеты по формуле:
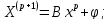
-
 *
*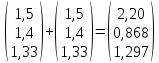 ;
;
 ;
;
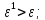
-
 *
*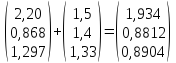 ;
;
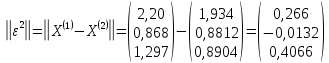 ;
;
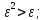
-
 *
*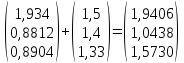 ;
;
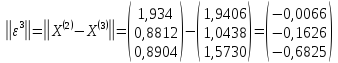 ;
;
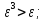
-
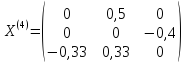 *
*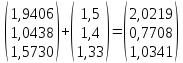 ;
;
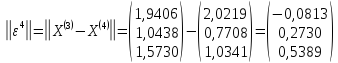 ;
;
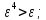
-
 *
*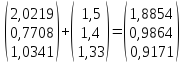 ;
;
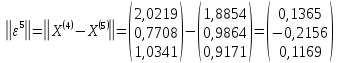 ;
;
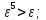
-
 *
*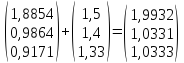 ;
;
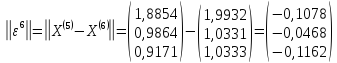 ;
;
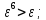
-
 *
*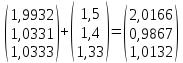 ;
;
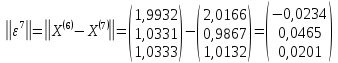 ;
;
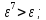
-
 *
*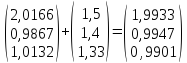 ;
;
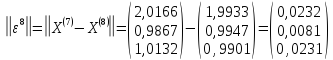 ;
;
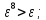
-
 *
*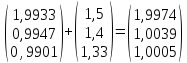 ;
;
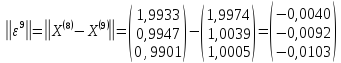 ;
;
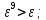
-
 *
*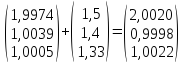 ;
;
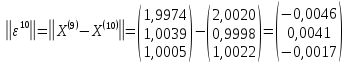 ;
;
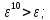
-
 *
*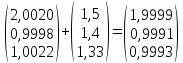 ;
;
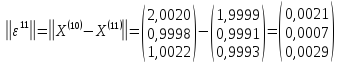 ;
;
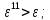
-
 *
*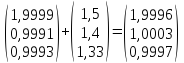 ;
;
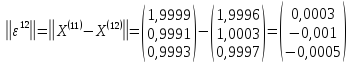 ;
;
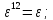
Ответ:
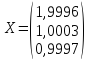 .
.
Задание №4
Методом
вращения с точностью
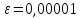 вычислить собственные значения и
собственные векторы симметрической
матрицы A.
вычислить собственные значения и
собственные векторы симметрической
матрицы A.
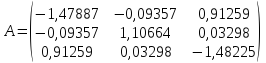
Решение
Положим:
 .
Выделим максимальный по модулю элемент
над главной диагональю
.
Выделим максимальный по модулю элемент
над главной диагональю
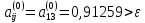 ;
;
Найдем угол поворота:
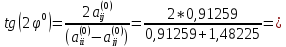 539,99408;
539,99408;
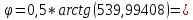 1,56894*0,5=0,78447;
1,56894*0,5=0,78447;
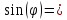 0,70645;
0,70645;
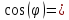 0,70776;
0,70776;
Сформируем матрицу вращения:
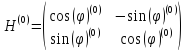

-
Выполним первую итерацию:
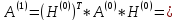
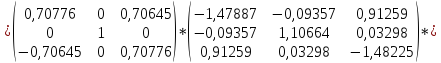
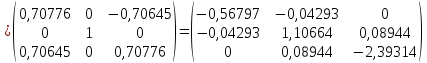
Т.к.
над главной диагональю максимальный
по модулю элемент
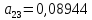 больше
больше
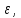 то
переходим к следующей итерации:
то
переходим к следующей итерации:
-
Найдем угол поворота:
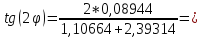 0,05111;
0,05111;
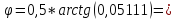 0,05107*0,5=0,02553;
0,05107*0,5=0,02553;
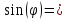 0,02553;
0,02553;
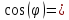 0,99967;
0,99967;
-
Сформируем матрицу вращения:

-
Выполним вторую итерацию:

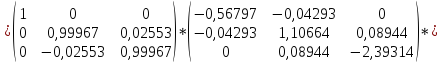
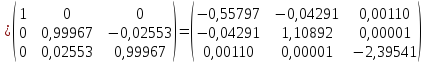
Т.к.
над главной диагональю максимальный
по модулю элемент
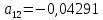 больше
больше
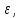 то
переходим к следующей итерации:
то
переходим к следующей итерации:
-
Найдем угол поворота:
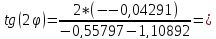 0,05118;
0,05118;
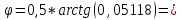 0,05114*0,5=0,02557;
0,05114*0,5=0,02557;
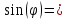 0,02556;
0,02556;
 0,99967;
0,99967;
-
Сформируем матрицу вращения:
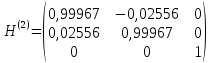
-
Выполним третью итерацию:
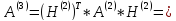
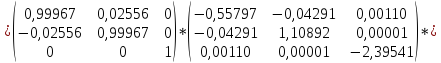
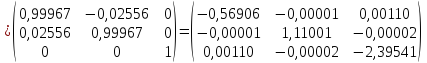
Т.к.
над главной диагональю максимальный
по модулю элемент
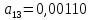 больше
больше
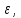 то
переходим к следующей итерации:
то
переходим к следующей итерации:
-
Найдем угол поворота:
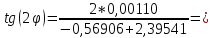 0,00120;
0,00120;
 0,00120*0,5=0,0006;
0,00120*0,5=0,0006;
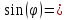 0,
00059;
0,
00059;
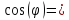 0,99999;
0,99999;
-
Сформируем матрицу вращения:

-
Выполним четвертую итерацию:
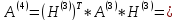

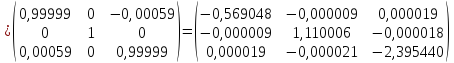
Т.к.
над главной диагональю максимальный
по модулю элемент
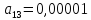 равен
равен
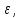 то
собственные
числа:
то
собственные
числа: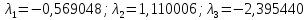 .
.
Найдем
собственные вектора:
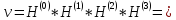
=

 =
=
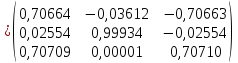
Ответ: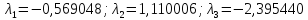 ;
;
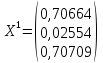 ;
;
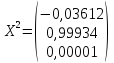 ;
;
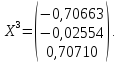
Задание №5
Найти
методом скалярных произведений с
точностью
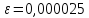 максимальное
по модулю собственное число
максимальное
по модулю собственное число
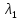 матрицы А и соответствующий ему
собственный вектор
матрицы А и соответствующий ему
собственный вектор
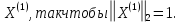
Проверить,
вычислив невязку
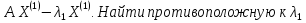 границу спектра собственных чисел.
границу спектра собственных чисел.
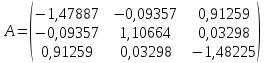
Решение
Начальное
приближение:
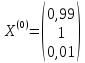 ;
;
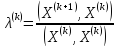
 ;
;
 ;
;
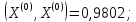
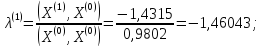
 ;
;
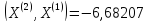 ;
;
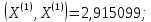
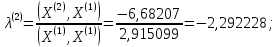
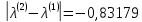 ;
;
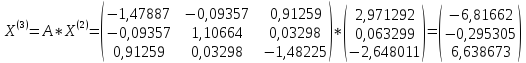 ;
;
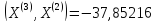 ;
;
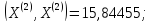
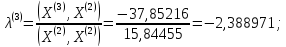
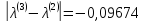 ;
;
 ;
;
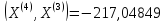 ;
;
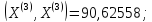
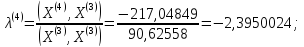
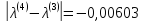 ;
;
 ;
;
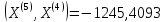 ;
;
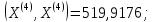
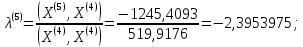
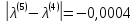 ;
;
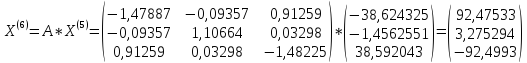 ;
;
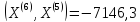 ;
;
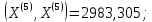
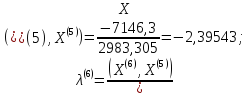
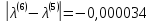 ;
;
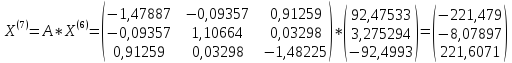 ;
;
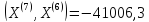 ;
;
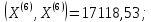
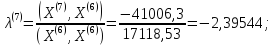
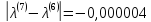 <
< .
.
Максимальное
по модулю собственное число:
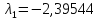 .
.
Невязка: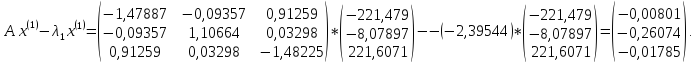
Найдем
противоположную к
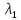 границу спектра собственных чисел. Для
этого построим матрицу
границу спектра собственных чисел. Для
этого построим матрицу
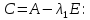
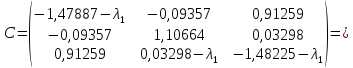
 ;
;
Произведем
аналогичные вычисления, взяв начальное
приближение
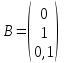 .
.
 ;
;
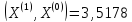 ;
;
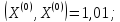

 ;
;
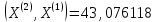 ;
;
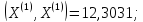
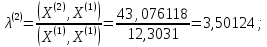
 ;
;
 ;
;
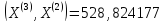 ;
;
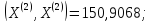
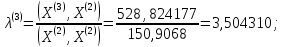
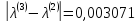 ;
;
 ;
;
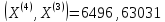 ;
;
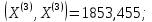
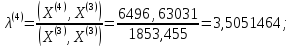
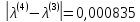 ;
;
 ;
;
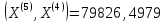 ;
;
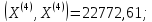
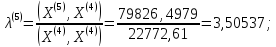
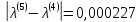 ;
;
 ;
;
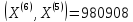 ;
;
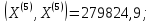
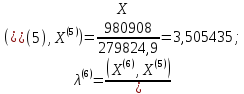
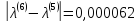 ;
;
 ;
;
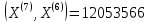 ;
;
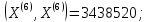
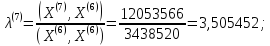
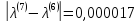 <
<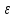 .
.
Искомое
собственное значение:
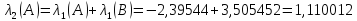 .
.
Ответ: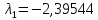 ,
,
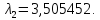
Задание №6
Методами
простых итераций и Ньютона найти корни
уравнения с точностью
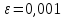 :
: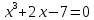 .
.
Для отделения корней преобразуем уравнение к равносильному виду
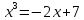 и
найдем точки пересечения графиков
и
найдем точки пересечения графиков
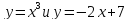 .
Корень уравнения принадлежит отрезку
[1,2].
.
Корень уравнения принадлежит отрезку
[1,2].
Решение методом простых итераций
Корень
уравнения принадлежит отрезку
[1,2].Преобразуем уравнение к виду
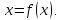 Для
этого запишем его в форме
Для
этого запишем его в форме
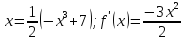
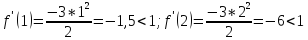 ,
следовательно, функцияне удовлетворяет
условию сходимости, сделаем другое
преобразование:
,
следовательно, функцияне удовлетворяет
условию сходимости, сделаем другое
преобразование:

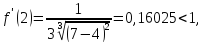 следовательно,функция
удовлетворяет условию сходимости.
следовательно,функция
удовлетворяет условию сходимости.
Зададим
начальное приближение
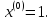 Выполним
расчеты по формуле:
Выполним
расчеты по формуле:
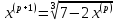 ,
p=0,1,2,…
.Результаты
расчетов:
,
p=0,1,2,…
.Результаты
расчетов:
|
p |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
1 |
1,4422 |
1,6025 |
1,5598 |
1,5714 |
1,5683 |
1,5691 |
1,5689 |
1,5689 |
|
|
- |
-0,5578 |
0,1603 |
-0,0427 |
0,0116 |
-0,0031 |
0,0009 |
-0,0002 |
0,0001 |
Ответ: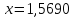 .
.
Решение методом Ньютона
Корень уравнения принадлежит отрезку [1, 2].
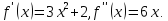 Зададим
начальное приближение
Зададим
начальное приближение
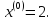 В
этой точке
В
этой точке
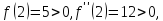 следовательно,
следовательно,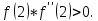 Выполним расчеты по формуле
Выполним расчеты по формуле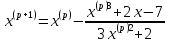 :,
p=0,1,2,…
Результаты
расчетов:
:,
p=0,1,2,…
Результаты
расчетов:
|
p |
0 |
1 |
2 |
3 |
4 |
|
|
2 |
1,6429 |
1,5716 |
1,5689 |
1,56895 |
|
|
- |
-0,3571 |
-0,0713 |
-0,0026 |
-0,000003 |
Ответ: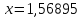 .
.
Задание №7
Выписать
интерполяционный многочлен Ньютона
для узловых значений
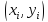 ,
заданных функцией
,
заданных функцией
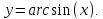 Найти
погрешность в точке
Найти
погрешность в точке
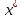 = 0.1,
= 0.1,
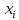 =
-0.5,-0.4,-0.3,-0.1,0,0.2
=
-0.5,-0.4,-0.3,-0.1,0,0.2
Решение
Значения
функции в точках
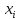 =
-0.5,-0.4,-0.3,-0.1,0,0.2
=
-0.5,-0.4,-0.3,-0.1,0,0.2
|
i |
0 |
1 |
2 |
3 |
4 |
5 |
|
xi |
-0,5 |
-0,4 |
-0,3 |
-0,1 |
0 |
0,2 |
|
f(xi) |
-0,5236 |
-0,412 |
-0,305 |
-0,1 |
0 |
0,2014 |
Вычислим
коэффициенты из формулы:
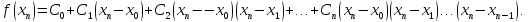
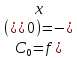 0,5236;
0,5236;
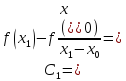 1,1208;
1,1208;
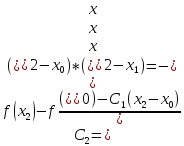 0,0026
0,0026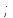
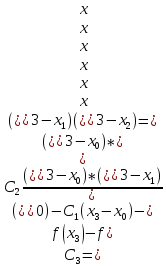 -1,0239;
-1,0239;
Аналогично
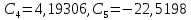 .
.
Построим интерполяционный полином Ньютона по формуле:
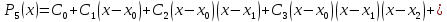
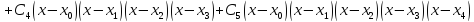
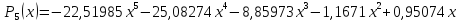
Вычислим
значение функции в точке
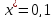 :
:
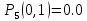 718098.
Значение функции
718098.
Значение функции
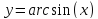 в этой же точке:
в этой же точке:
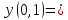 0,1001674.
0,1001674.
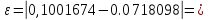 0,028358.
0,028358.
Ответ:
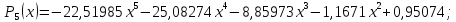
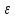 =0,028358.
=0,028358.
Задание №8
Вычислить
решение методом Рунге-Кутты-Мерсона с
точностью
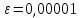 .
Построить график решения в Matlab.
.
Построить график решения в Matlab.
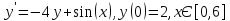
Головная программа
clc
% Метод Рунге-Кутты-Мерсона
options = odeset ('RelTol', 1e-5);
[T,Y] = ode45(@MyFunction,[0 6], 1, options);
plot(T,Y(:,1),'-')
Функция
functiondy = MyFunction(x,y)
dx = zeros(3,1);
k(1) = -4;
dy(1) = k(1)*y+sin(x);
График представлен на рисунке 1.
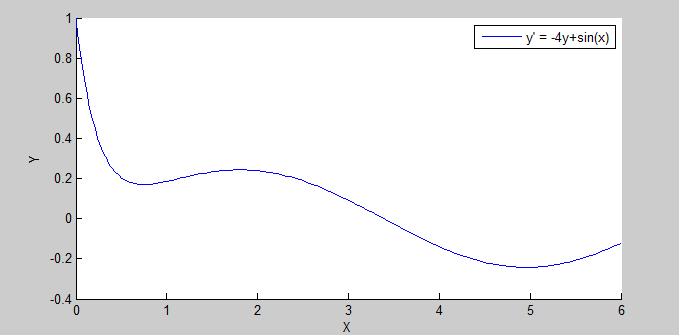
Рисунок 1