
Численные методы / РГР ЧМ 10 вариант
.docxЗадание №6
Методами
простых итераций и Ньютона найти корни
уравнения с точностью
 :
:
 .
.
Решение методом простых итераций
Корень уравнения принадлежит отрезку [5; 5.3].
f(5)
=
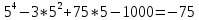 .
.
f(5.3)
=
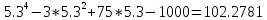 .
.
Преобразуем
уравнение к виду
 Для
этого сначала запишем его в форме
Для
этого сначала запишем его в форме
 .
.
Возьмем производную:

Найдем решение в точках на концах отрезка:
 следовательно,
функция не удовлетворяет условию
сходимости, сделаем другое преобразование:
следовательно,
функция не удовлетворяет условию
сходимости, сделаем другое преобразование:

Возьмем производную:

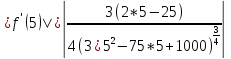 =
0.082666394 <1
=
0.082666394 <1
 =
0.080503594 <1
=
0.080503594 <1
Т.к. значения производной в точках на концах отрезка по модулю меньше единицы, следовательно, функция удовлетворяет условию сходимости.
Зададим
начальное приближение
 Выполним расчеты по формуле:
Выполним расчеты по формуле:
 ,
p=0,1,2,…
. Результаты
расчетов в таблице 3:
,
p=0,1,2,…
. Результаты
расчетов в таблице 3:
Таблица 4.
|
P |
0 |
1 |
2 |
3 |
4 |
5 |
|
x(p) |
5.15 |
5.131367 |
5.132888 |
5.132764 |
5.132774 |
5.132773 |
|
|x(p+1)-x(p)| |
- |
0.018633 |
0.001522 |
0.000124 |
0.00001 |
0.000001 |
Ответ:
 5,132773.
5,132773.
Решение методом Ньютона

Корень уравнения принадлежит отрезку [5; 5.3].
 Зададим
начальное приближение
Зададим
начальное приближение
 В
этой точке
В
этой точке
 следовательно,
следовательно,
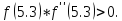 Выполним расчеты по формуле:
Выполним расчеты по формуле:
 ,
p=0,1,2,…
,
p=0,1,2,…
Результаты расчетов в таблице 5.
Таблица 5.
|
P |
0 |
1 |
2 |
3 |
4 |
|
x(p) |
5.15 |
5.132852 |
5.132773 |
5.132773 |
5.132773 |
|
|x(p+1)-x(p)| |
- |
0.0171484 |
7.8929*10(-5) |
1.625*10(-9) |
0 |
Ответ:
 5.132773.
5.132773.
Задание №7
Выписать
интерполяционный многочлен Ньютона
для узловых значений
 ,
заданных функцией
,
заданных функцией
 Найти
погрешность в точке
Найти
погрешность в точке
 = -0.4,
= -0.4,
 =
0,0.1,0.2,0.4,0.5,0.8
=
0,0.1,0.2,0.4,0.5,0.8
Решение
Таблица 6.
|
i |
0 |
1 |
2 |
3 |
4 |
5 |
|
xi |
0 |
0.1 |
0.2 |
0.4 |
0.5 |
0.8 |
|
f(xi) |
0 |
0.001745 |
0.003491 |
0.006981 |
0.008727 |
0.013962 |
Вычислим коэффициенты по формулам:
 0;
0;
 0.01745
0.01745
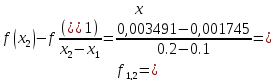 0,01746
0,01746
 0.01745;
0.01745;
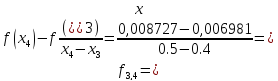 0.01746;
0.01746;
 0,01745;
0,01745;
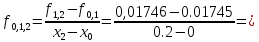 0.00005
0.00005
 0,0000333
0,0000333
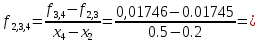 0,0000333
0,0000333
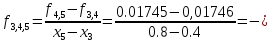 0,000025
0,000025
 0.0002083
0.0002083
 0,0001665
0,0001665
 0,0000972
0,0000972
 0,0007495
0,0007495
 0,0003766
0,0003766
 0.001407625
0.001407625
Построим интерполяционный многочлен Ньютона по формуле:








 0.001464
0.001464
Вычислим
значение функции в точке
 :
:
 6829228.
Значение функции
6829228.
Значение функции
 в этой же точке:
в этой же точке:
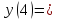 0,0697565.
Погрешность:
0,0697565.
Погрешность:
 0,001464.
0,001464.
Ответ:

 погрешность:
0, 001464.
погрешность:
0, 001464.
Задание №8
Вычислить
решение методом Рунге-Кутты-Мерсона с
точностью
 .
Построить график решения в Matlab.
.
Построить график решения в Matlab.

Текст программы:
function dy = vdp3000(x,y)
dy = zeros(1,1); % a column vector
dy=(0.6-(y^2))*cos(x)+0.2*y;
[X,Y] = ode45(@vdp3000,[0 1],0);
plot(X,Y(:,1),'-o')
График
решения представлен на рисунке 1.
Рисунок 1. График решения уравнения y’
Новосибирск, 2013
