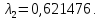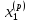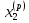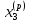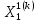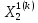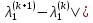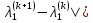Численные методы / РГР ЧМ 10 вариант
.docxМинистерство образования и науки Российской Федерации
Федеральное агентство по образованию
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Факультет бизнеса
Кафедра экономической информатики
Расчетно-графическая работа
по дисциплине «Численные методы»
Вариант 10
Выполнила:
Суслина Д. В.
Группа:
ФБИ-11
Проверила:
Соболева О.Н.
Задание №1
Записать порядок выполняемых вами операций, оценить погрешность их результатов, вычислить и записать искомое значение. Определить число верных знаков.
.
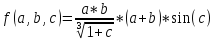
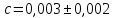Решение
-
Приближенные значения исходных данных:
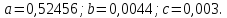
Абсолютные погрешности исходных данных:
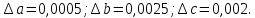
Найдем относительные погрешности исходных данных по формуле:
(1.1)
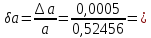0,00095318;
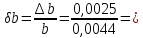0,568181818;
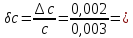0,666666667.
-
Порядок выполняемых операций:
Выполняем действия в соответствии с формулами для определения погрешности результатов арифметических операций:
Погрешность суммы:
(1.2)
Пусть
,
тогда
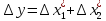
Погрешность разности:
(1.3)
Пусть
,
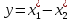тогда
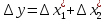
Погрешность произведения:
(1.4)
Пусть
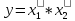, известны
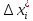и
,
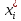i=1,2
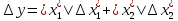
Погрешность частного:
(1.5)
Пусть
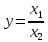, тогда
Из формул (1.2) – (1.5) выводятся формулы для соответствующих относительных погрешностей:
-
a*b = 0.52456*0.0044 = 0.0023081
|a|*
a
+ |b|*
b
=
0.0013136;
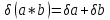= 0.5691350
-
1+с = 1,003
;
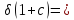
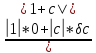
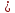0,0019940108
-
(1+с)^(1/3) = 1,000999002
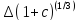=((1+с)^(1/3))’*
=
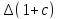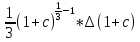= 0.000663347;
=
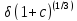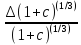= 0,000662685
-
(a+b) = 0.52896
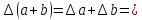0.003;
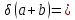
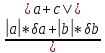
0.005671506
-
Sin(c) = 0.002999996
=
(sin(c))’*
= 0.001999991;
=
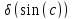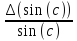= 0.666664667
-
L=
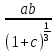= 0.002305761
=
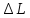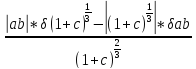= 0.000274535;
=
=
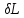0,569797683
-
D=L*(a+b)=0.001219655
=
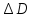|L|*
L
+ |a+b|*
(a+b)
= 0.000122135;
=
=
0.575469189
-
F=D*sin(c) = 0.00000365
=
1.242133856
=
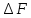F*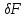
= 0.000004545
-
Определение числа верных знаков:
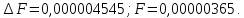
Пусть А – точное число, тогда а – приближенное число.
Определим веерные знаки с помощью формулы:
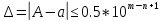
m – старший десятичный разряд числа.
.
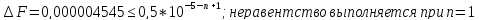Верные знаки: 3.
Ответ:
Число
верных знаков n=1.
.
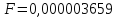Задание №2
Выяснить погрешность задания исходных данных, необходимую для получения результата с m верными значащими цифрами.
;
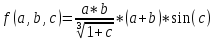
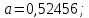
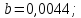
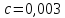m
= 4
Решение
Из
предыдущего задания:
,
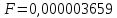при m
= 4 верные знаки: 3;6;5;9.
Тогда
Для определения числа верных знаков воспользуемся определением и оценкой для абсолютной погрешности функции.
(1.6)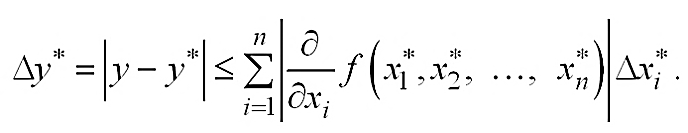
= 0.00001389
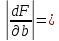
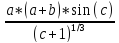= 0.000831582
= 0.001218434
=
=
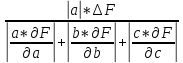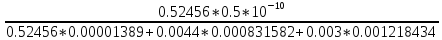= 0.000017962
=
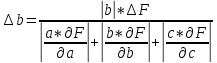0.000000151
=
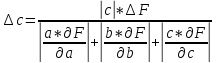0.000000103
Ответ:
Задание №3
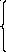Решить
СЛАУ методом Гаусса и с точностью до
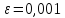методом
простой итерации.
;
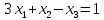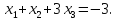
Решение методом Гаусса.
-
Запишем систему в виде расширенной матрицы и приведем матрицу к треугольному виду с помощью элементарных преобразований:
=>
=>
=> =>
=>
=>
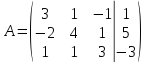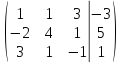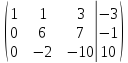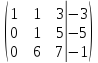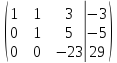По матрице А составим уравнение:
=
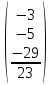
Отсюда:
=
-1,26087;
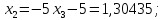
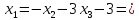-0.52174
Ответ:
-0.52174,
,
-1,26087.
Решение методом простой итерации
-
Исходная матрица имеет диагональное преобладание:
=
-
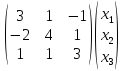Выразим
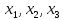из первого, втрого и третьего уравнений
соответственно:
;
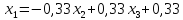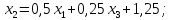
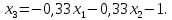
Тогда матрица примет вид:
;
-
Норма
значит
матрица сходится.
-
Зададим начальное приближение:
;
-
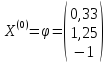Выполним расчеты по формуле:
*
;
;
*
;
;
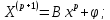
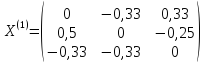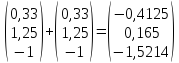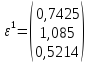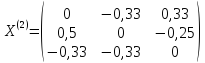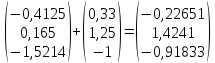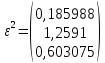Результаты дальнейших итераций занесем в таблицу (Таблица 1).
Таблица 1.
|
p |
|
|
|
|
|
3 |
-0.443 |
1.366325 |
-1.3952 |
0.476879 |
|
4 |
-0.5813 |
1.377301 |
-1.3047 |
0.138304 |
|
5 |
-0.55506 |
1.285522 |
-1.26268 |
0.091779 |
|
6 |
-0.51091 |
1.28814 |
-1.24105 |
0.044153 |
|
7 |
-0.50463 |
1.30481 |
-1.25649 |
0.016670 |
|
8 |
-0.51523 |
1.311805 |
-1.26406 |
0.010594 |
|
9 |
-0.52003 |
1.308401 |
-1.26287 |
0.004807 |
|
10 |
-0.51852 |
1.3057 |
-1.26016 |
0.002710 |
|
11 |
-0.51673 |
1.30578 |
-1.25977 |
0.001785 |
|
12 |
-0.51663 |
1.306575 |
-1.26039 |
0.000795 |
Ответ:
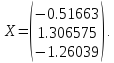0,001792089615762 =
Задание №4
Методом
вращения с точностью
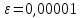вычислить собственные значения и
собственные векторы симметрической
матрицы A.
-
Положим:
.
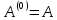Выделим максимальный по модулю элемент
над главной диагональю
; -
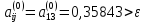Найдем угол поворота:
117,8852162;
0,781156851;
0,7041014;
0,7100099;
-
Сформируем матрицу вращения:
-
Выполним первую итерацию:
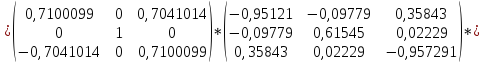
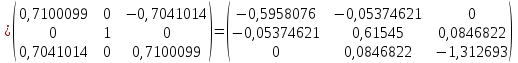
Так
как над главной диагональю максимальный
по модулю элемент
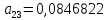больше
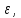то
переходим к следующей итерации:
-
Найдем угол поворота:
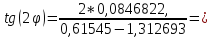0,087838;
0,043807;
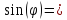0,0437926;
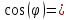0,9990406;
-
Сформируем матрицу вращения:
-
Выполним вторую итерацию:
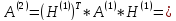
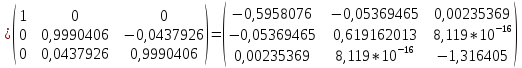
Так
как над главной диагональю максимальный
по модулю элемент
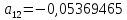больше
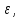то
переходим к следующей итерации:
-
Найдем угол поворота:
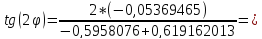0,088388459;
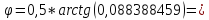0,044079677;
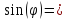0,044065403;
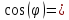0,999028648;
-
Сформируем матрицу вращения:
-
Выполним третью итерацию:
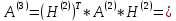
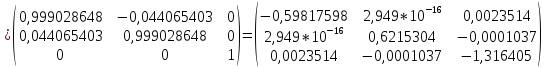
Так
как над главной диагональю максимальный
по модулю элемент
больше
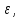то
переходим к следующей итерации:
-
Найдем угол поворота:
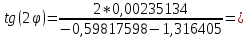0,006547767;
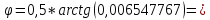0,003273837;
0,
003273831;
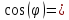0,999994641;
-
Сформируем матрицу вращения:
-
Выполним четвертую итерацию:
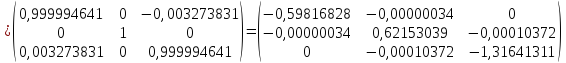
Так
как над главной диагональю максимальный
по модулю элемент
больше
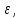то
переходим к следующей итерации:
-
Найдем угол поворота:
0,000107037;
0,0000532;
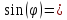0,0000532;
0,9999999;
-
Сформируем матрицу вращения:
-
Выполним пятую итерацию:
Максимальный
по модулю элемент
ательно,
для решения задачи потребовалось 5
итераций.
Собственные
числа: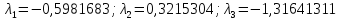
.
Найдем
собственные вектора:
=
*
=
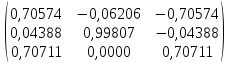
Ответ:
;
;
;
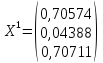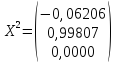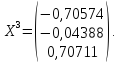
Задание №5
Найти
степенным методом с точностью
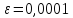максимальное по модулю собственное
число
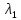матрицы А
и
соответствующий ему собственный вектор
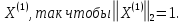
Проверить
вычислив невязку
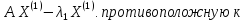
границу спектра собственных чисел.
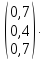
Выбираем начальное приближение собственного вектора
=
Чтобы вычислить собственный вектор воспользуемся формулой:
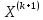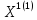=A
=
A
=
*
=
=
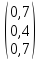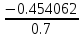= 4.643236
Выполним следующую итерацию:
=
A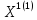
=
*
=
=
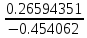= -0.5857
Так
как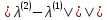
-0.5857
- 4.643236| = 5.228934 >
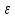, то процесс вычисления необходимо
продолжить. Результаты вычислений в
таблице 2.
Таблица 2.
|
P |
|
|
|
|
| |
|
3 |
-0.184062866 |
0.074144931 |
-0.125555724 |
-0.69211 |
0.024792 |
|
4 |
0.122828867 |
0.060833369 |
0.055872402 |
-0.66732 |
0.024792 |
|
5 |
-0.102758597 |
0.026673858 |
-0.008104621 |
-08366 |
0.16928 |
|
6 |
0.092231629 |
0.026284537 |
-0.028478723 |
-0.89756 |
0.060957 |
|
7 |
0.100509642 |
0.006522696 |
0.060906891 |
-1.16207 |
0.072313 |
|
8 |
0.116798779 |
-0.146345708 |
0.1870506936 |
-1.27819 |
0.025212 |
|
9 |
-0.146345708 |
-0.004165796 |
0.132366326 |
-1.25297 |
0.090908 |
|
10 |
0.187056936 |
0.014697753 |
-0.17926064 |
-1.27819 |
0.025212 |
|
11 |
-0.243620113 |
-0.013242285 |
0.238979028 |
-1.30238 |
0.024199 |
|
12 |
0.318686104 |
0.021000489 |
-0.31638884 |
-1.30813 |
0.005742 |
|
13 |
-0.418594141 |
-0.025291861 |
0.417570529 |
-1.3135 |
0.005373 |
|
14 |
0.550314029 |
0.034676093 |
-0.550336963 |
-1.31467 |
0.001172 |
|
15 |
-0.72411246 |
-0.044740819 |
0.724854609 |
-1.31582 |
0.001145 |
|
16 |
.0952967855 |
0.05943223 |
-0.954437696 |
-1.31605 |
0.000233 |
|
17 |
-1.254383535 |
-0.077887577 |
1.256571629 |
-1.31629 |
0.000242 |
|
18 |
1.651191757 |
0.102739238 |
-1.65429516 |
-1.31634 |
0.000046 |
Невязка:
-1,
31634)*
;
Максимальное
по модулю собственное число:
-
.
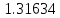Найдем
противоположную границу спектра
собственных чисел. Для этого построим
матрицу
;
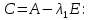
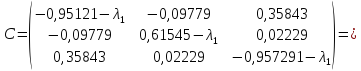
Произведем
аналогичные вычисления, взяв начальное
приближение
=
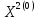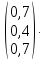
Таблица 3.
|
P |
|
|
|
|
| |
|
1 |
0,467376 |
0,719866 |
0,5111513 |
1,799665 |
1,799565 |
|
2 |
0,283469 |
1,356319 |
0,3670958 |
1,884127 |
0,084462 |
|
3 |
0,102447 |
2,600585 |
0,2636416 |
1,917385 |
0,033258 |
|
4 |
-0,122408 |
5,019643 |
0,1893473 |
1,930197 |
0,012813 |
|
5 |
-0,467698 |
9,713087 |
0,1359982 |
1,935015 |
0,004818 |
|
6 |
-1,0718675 |
18,81241 |
0,0976978 |
1,936811 |
0,001795 |
|
7 |
-2,1960188 |
36,44862 |
0,0702175 |
1,937478 |
0,000667 |
|
8 |
-4,3409752 |
70,6274 |
0,0505323 |
1,937725 |
0,000247 |
|
9 |
-8,4735614 |
136,8629 |
0,0364926 |
1,937816 |
0,000092 |
Искомое
собственное значение:
+
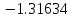1,937816=
0,621476
Ответ:
,
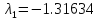