Розділ 9
9.1.
Тоді
9.2.
Скористаємось теоремою Пуассона:
а)
б)
в)
г)
9.3. а) 0,18045; б) 0,32332; в) 0,13534.
9.4. а)
б)
в)
г)
9.5.
9.6.
і
Розпишемо першу нерівність
Після скорочення дістанемо
тобто
Аналогічно розписуючи другу нерівність,
дістанемо
9.7.
9.8. а)
б)
9.9. 24 або 25.
9.10.
при великих
Тут використовувались комбінаторна
тотожність
і формула Стірлінга
9.11.
Скористатися теоремою Пуассона.
а)
б)
в)
9.12.
Аналогічно задачі 9.11:
9.13. 0,43348.
9.14. Скористатися локальною теоремою Муавра—Лапласа.
а) 0,0532; б) 0,0219.
9.15. В
силу інтегральної теореми Муавра—Лапласа
Значення
з точністю
9.16. а) 0,0005; б) 0,9510; в) 0,9043.
9.17.
9.18.
9.19.
9.20.
Тут використали такі рівності:
9.21. Необхідність. Нехай має геометричний розподіл, тоді
.
Достатність.
Нехай виконується рівність задачі.
Позначимо
.
Тоді
Отже,
Нехай
тоді
що і треба було довести.
9.
22.
9.
23.
9.24.
і
9.25.
9.26.
а)
;
б) див. задачу 9.23.
9.27.
9.28.
Розподіл Паскаля є геометричним
розподілом з
Тоді
9.29.
Розділ 10
10.1. в), г), д).
10.2.
10.3.
а) Не може бути щільністю; б)
10.4.
10.5.
Рівномірний розподіл на
10.6.
а)
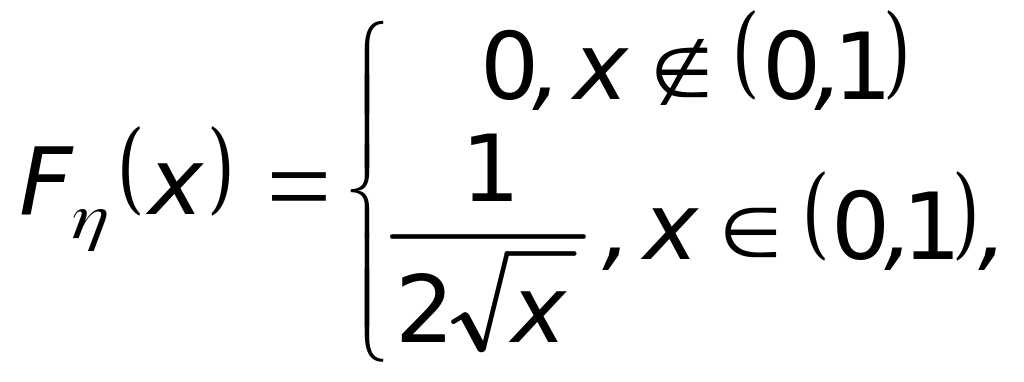
б)
в)
10.7. Рівномірний розподіл на
10.8.
а)
б)
10.9.
а)
б)
в)
10.10.
Рівномірний розподіл на
10.11. Рівномірний розподіл на
10.12.
10.13.
10.14.
Нехай
Тоді
=
.
Якщо ж,
то
10.15.
Рівномірний розподіл на
.(Див. задачу 10.7).
10.16.
10.17.
10.18.
10.19.
10.20.
10.21.
а)
б)
в)
10.22.
а)
б)
10.23.
а)
б)
10.24.
10.25.
10.26.
10.27.
а)
б)
10.28.
10.29.
.
10.30.
Скористаємося нерівністю
10.31.
10.36.
10.37.
а)
б)
в)
10.38.
а)
б)
10.39.
10.42.
а)
б)
в) не існує.
10.43.
Позначимо
Тоді
10.44—10.45. Доведення провести, використовуючи метод математичної індукції.
10.46.
10.48.
10.49.
10.50.
а) 0;
б)
10.51.
10.52. а) так; б) не завжди; наприклад,
а
Ці
випадкові величини попарно некорельовані,
але
Розділ 11
11.1. а), б), г), е), є) – виконуються; в), д) – не виконуються.
11.2.
11.3.
за ймовірністю в силу ЗВЧ. Тут використали
те, що
і
за ймовірністю.
11.4.
11.5.
Нехай
— послідовність незалежних однаково
розподілених випадкових величин з
рівномірним розподілом на
.
В силу ЗВЧ
за ймовірністю і
за ймовірністю для будь-якої неперервної
функції. Згідно з теоремою Лебега, якщо
— обмежена функція, то
Але
11.6.
11.7.
11.8. –1.
11.9. Закон великих чисел та центральна гранична теорема виконуються.
11.10.
При
при
При
,
а при
обмежена при
Аналогічно
при
а при
,
і при
обмежена.
Оскільки
при
,
то
і умова Ляпунова виконана. При
не виконується умова рівномірної
малості.
При
також
11.11. Не виконується.
11.12.
Розділ 12
12.1. а) 2,2,2,3,3,3,4,4,4,4,5,5,7,10,10;
б
)
2 3
4 5
7 10
3 3 4 2 1 2
12.2. а)
б)
12.3.
.
Розділ 13
13.1.
13.2.
13.3.
13.4.
Скористатися тим, що
13.5.
Скористатися тим, що
має розподіл
13.6.
Скористатися тим, що
має розподіл
13.7.
13.8.
Незміщеними і спроможними оцінками
будуть статистики
і
незміщеною і спроможною оцінкою для
буде статистика
Використати результати задачі 12.4.
13.9.
13.10.
13.11.
Показати, що
Розділ 14
14.1.
Скористатися тим, що
14.6.
14.7.
14.8.
має розподіл Пуассона з параметром
14.9.
14.10.
.
Розділ 15
15.1. — незміщена та спроможна оцінка.
15.2.
— незміщена і спроможна оцінка.
15.3.
де
15.4.
Оцінка максимальної правдоподібності
—
15.5.
— незміщена й ефективна оцінка.
15.6.
де
Ці оцінки спроможні. У числовому прикладі
15.7.
15.8.
15.11.
— незміщена й ефективна оцінка.
15.12.
— спроможна оцінка.
Розділ 16
16.1.
16.2.
16.3.
16.4.
16.5. a)
б)
16.6. а)
16.7.
16.8.
16.10.
16.11.
Розділ 17
17.1. а)
гіпотеза приймається.
17.3.
б)
гіпотеза приймається;
д)
гіпотеза
приймається.
17.4.
гіпотеза приймається.
17.5.
гіпотеза приймається.
17.6.
гіпотеза однорідності приймається.
17.7.
гіпотеза однорідності приймається.
17.8.
гіпотеза незалежності відхиляється.
17.9.
гіпотеза незалежності
відхиляється.
17.10.
гіпотеза незалежності приймається.
17.11.
гіпотеза однорідності приймається.
17.12.
гіпотеза приймається.