Розділ 21. Елементи аналізу часових рядів. Виділення тренду, згладжування, прогноз

Адитивна модель часового ряду

де

— детермінована складова (тренд),

— сезонні коливання,

— нерегульований або залишковий компонент (випадкова складова),

Мультиплікативна модель:

Виділення тренду. Нехай — незалежні випадкові величини з

Для виділення тренду застосовується метод найменших квадратів. Наприклад, якщо то і знаходити з

Аналогічно використовується метод найменших квадратів у випадку поліноміального тренду:

Зважене згладжування. або

де — наперед задане число.

Експоненціальне згладжування. Цей метод дає змогу аналізувати часовий ряд і отримувати прогнози без попереднього задання форми тренду. Вимагається лише, щоб у множині дослідження тренд змінювався досить поступово.

де або

Прогнози:

Метод згладжування Холта—Вінтерса. Нехай — трендова компонента, а — приріст. Тоді

Прогноз часового ряду:

Нехай тепер — стаціонарний процес.

Модель авторегресії AR(p):

Коефіцієнти можна оцінити методом найменших квадратів. Наприклад, для AR(1) маємо:

і прогноз .

Модель рухомого середнього МА(q):

Модель ARMA(p, q):

Міри точності прогнозів. Якщо — часовий ряд, а — прогнозне значення, то

— середньоквадратична похибка прогнозу за n кроків.

— середня абсолютна похибка.

— корінь із середньоквадратичної похибки у відсотках від фактичних значень.

— середня абсолютна похибка у відсотках.

Приклад розв’язання задачі

Задача 1. У таблиці наведено щорічні значення виробництва пива у США за 1970—1989 рр. Методом експоненціального згладжування (w=0,7 та ) та методом Холта—Вінтерса ( та ) побудувати прогнози значень виробництва пива на 1987—1989 рр, використовуючи дані за 1970—1986 рр. Підрахувати похибки

Розв’язок. Спочатку підрахуємо експоненціально згладжені значення E₁, E₂, …, E_t для років 1970—1986.

Для

Інші значення подано в таблиці.

Для

Інші значення подано в таблиці.

Рік	Виробництво пива	Експоненціально згладжене значення,	Експоненціально згладжене значення,
1970	133,1	133,10	133,10
1971	137,4	134,39	136,11
1972	141,3	136,46	139,74
1973	148,6	140,10	145,94
1974	156,2	144,93	153,12
1975	160,6	149,63	158,36
1976	163,7	153,85	162,10
1977	170,5	158,85	167,98
1978	179,1	164,92	175,76
1979	184,2	170,71	181,67
1980	194,1	177,72	190,37
1981	193,7	182,52	192,70
1982	196,2	186,62	195,15
1983	195,4	189,26	195,33
1984	192,2	190,14	193,14
1985	194,3	191,39	193,95
1986	194,4	192,29	194,27
1987	195,9
1988	197,4
1989	197,8

Використовуючи експоненціальне згладжування, отримаємо такі прогнозні значення.

Для

похибка прогнозу

похибка прогнозу

похибка прогнозу

Для

похибка прогнозу

похибка прогнозу

похибка прогнозу

Тепер обчислимо значення за методом Холта—Вінтерса за 1970—1986 рр.

Для та

Інші значення та подано в таблиці.

Для та

Інші значення та подано в таблиці.

Рік	Виробництво пива
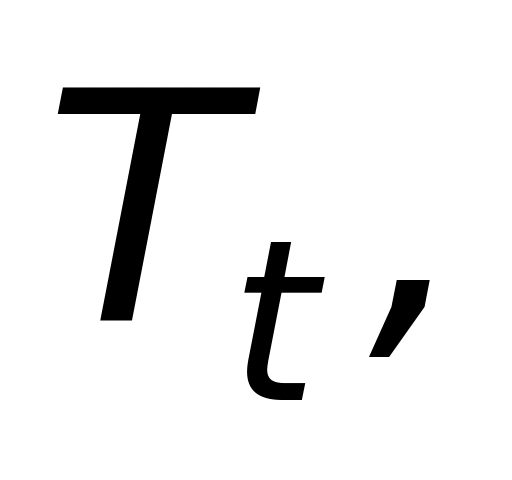
1970	133,1
1971	137,4	137,40	4,30	137,40	4,30
1972	141,3	141,42	4,22	141,58	4,22
1973	148,6	147,71	4,84	146,64	4,80
1974	156,2	155,10	5,61	152,87	5,80
1975	160,6	160,63	5,58	159,25	6,21
1976	163,7	164,45	5,05	164,93	5,84
1977	170,5	170,20	5,26	170,69	5,78
1978	179,1	178,01	6,03	177,26	6,33
1979	184,2	184,15	6,06	183,78	6,46
1980	194,1	192,93	6,88	191,40	7,27
1981	193,7	195,53	5,59	197,18	6,23
1982	196,2	197,68	4,56	201,24	4,72
1983	195,4	197,45	3,12	202,79	2,50
1984	192,2	194,71	1,36	201,36	–0,25
1985	194,3	194,83	0,99	199,07	–1,68
1986	194,4	194,83	0,69	196,49	–2,31
1987	195,9
1988	197,4
1989	197,8

Далі будуємо прогнози за методом Холта—Вінтерса.

Для та

похибка прогнозу

похибка прогнозу

похибка прогнозу

Для та

похибка прогнозу

похибка прогнозу

похибка прогнозу

Тепер підрахуємо похибки прогнозів.

Для експоненціального згладжування при

Для експоненціального згладжування при

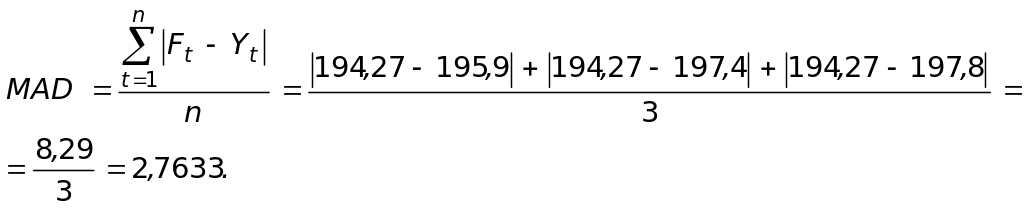
Для методу Холта—Вінтерса при та

Для методу Холта—Вінтерса при та

Слід зазначити, що обидва значення для прогнозів за методом експоненціального згладжування та лежать між значеннями для прогнозів за методом Холта—Вінтерса ( та ). Аналогічно, для прогнозів за методом експоненціального згладжування та лежать між для прогнозів за методом Холта—Вінтерса та

Можна сказати, що існує трендовий компонент у часовому ряду виробництва пива. Дані збільшуються кожного року з 1970 по 1980 рр, потім зростають та спадають протягом декількох років і знову збільшуються з 1985 року. Здається, що модель Холта—Вінтерса з параметрами та є найкращою для прогнозування обсягів виробництва пива. Ця модель має найменшу похибку.

Задачі

21.1. У таблиці наведено квартальні значення експорту послуг України за 1996—1998 роки. а) Методом експоненціального згладжування (=0,8); б) методом Холта—Вінтерса ( ) побудувати прогнози значень експорту послуг на 1998 рік, використовуючи дані за 1996—1997 роки. Підрахувати похибки

Статті платіжного балансу	1996 р.				1997 р.				1998 р
	І кв.	II кв.	III кв.	IV кв.	I кв.	II кв.	III кв.	IV кв.	І кв.	II кв.	III кв.	IV кв.
Баланс товарів та послуг	–702	65	–22	–463	–741	–354	–249	–192	–722	–261	–364	140
Експорт товарів та послуг	4667	5486	5068	5125	4744	5040	5205	5366	4421	4727	4147	4326
Імпорт товарів та послуг	5369	5421	5090	5588	5485	5394	5454	5558	5143	4988	4511	4186
Експорт товарів	3544	4208	3905	3890	3527	3858	3945	4088	3443	3750	3174	3332
Імпорт товарів	5050	5019	4624	5150	4983	4882	4830	4928	4459	4270	3868	3686
Баланс послуг	804	876	697	797	715	670	636	648	294	259	330	494
Експорт послуг	1123	1278	1163	1235	1217	1182	1260	1278	978	977	973	994
Імпорт послуг	319	402	466	438	502	512	624	630	684	718	643	500

21.2. У таблиці наведено квартальні значення імпорту послуг з України за 1996—1998 рр. Методами: а) експоненціального згладжування (=0,8); б) Холта—Вінтерса ( ) побудувати прогнози значень імпорту послуг на 1998 рік, використовуючи дані за 1996—1997 рр. Підрахувати похибки

21.3. У таблиці наведено квартальні значення балансу товарів та послуг з України за 1996—1998 рр. Методами: а) експоненціального згладжування (=0,8); б) Холта—Вінтерса ( ) побудувати прогнози значень балансу товарів та послуг на 1998 рік, використовуючи дані за 1996—1997 рр. Підрахувати похибки

21.4. У таблиці наведено квартальні значення експорту товарів України за 1996—1998 рр. Методами: а) експоненціального згладжування (=0,8); б) Холта—Вінтерса ( ) побудувати прогнози значень експорту товарів на 1998 рік, використовуючи дані за 1996—1997 рр. Підрахувати похибки

21.5. У таблиці наведено квартальні значення імпорту товарів України за 1996—1998 рр. Методами: а) експоненціального згладжування (=0,8); б) Холта—Вінтерса ( ) побудувати прогнози значень товарів послуг на 1998 рік, використовуючи дані за 1996—1997 рр. Підрахувати похибки

21.6. Припускаючи, що дані часових рядів стаціонарні, побудувати AR(1) для: а) експорту послуг; б) імпорту послуг; в) експорту товарів; г) імпорту товарів; д) балансу товарів та послуг. Побудувати прогноз на 1998 рік, використовуючи дані за 1996—1997 роки. Підрахувати похибки

21.7. Виділити лінійний тренд для імпорту послуг.