Розділ 16. Надійні інтервали

Нехай  — вибірковий вектор об'єму n, — розподіл вектора , який залежить від невідомого параметра . При інтервальному оцінюванні невідомого параметра  шукають такі дві статистики і в яких і для яких при заданому виконується умова:

Тоді інтервал називається (1–-надійним інтервалом, імовірність 1– — рівнем надійності, а і — нижньою та верхньою межами надійності.

Інтервал — асимптотично найкоротший (1–-надійний інтервал. Значення величин подано у таблиці 4 додатка.

Надійні інтервали для нормального розподілу

1. Надійний інтервал для математичного сподівання при відомій дисперсії:

2. Надійний інтервал для дисперсії якщо математичне сподівання a відоме:

де числа і такі, що

і (таблиця 5 додатка).

3. Надійні інтервали для дисперсії a та у випадку, якщо обидва параметри невідомі:

,

де знаходиться з таблиці Стьюдента (табл. 6 додатка) так, щоб де - число степенів свободи, і (таблиця 5 додатка).

Приклад розв'язання задачі

Задача 1. Нехай =(₁, ₂, …, _n) — вибірковий вектор з генеральної сукупності з розподілом Пуассона з параметром . Побудувати (1–-надійний інтервал.

Розв’язок. За умовою задачі

— реалізація вектора .

Оцінка максимальної правдоподібності знаходиться з рівняння:

і

Тоді (1–-надійний інтервал для параметра буде таким:

Задачі

16.1. Побудувати надійний інтервал для параметра  біноміального розподілу

16.2. Проведено 100 незалежних спостережень, у результаті яких подія A спостерігалась 40 разів. Визначити надійний інтервал для ймовірності виникнення події A при 1– = 0,95, якщо число виникнень події A має біноміальний розподіл.

16.3. На телефонній станції проводились спостереження за числом нeправильних з’єднань за хвилину. Спостереження протягом години дали такі результати:

xk	0	1	2	3	4	5	7
mk	8	17	16	10	6	2	1

Припускаючи, що число правильних з’єднань за хвилину має пуассонівський розподіл, знайти надійний інтервал для математичного сподівання розподілу з надійністю 0,99.

16.4. Побудувати надійний інтервал для параметра  нормального розподілу

16.5. Побудувати надійний інтервал для параметра  за вибіркою =(₁, ₂, …, _n) з генеральної сукупності з розподілом:

а) б)

16.6. Знайти надійні інтервали для параметрів a і ² нормального розподілу за вибіркою:

а) 0,6; 2,4; 2,1; 1,4; 1,2; 4,8; 0,9; 1,1; 3,5; 3,0; 0,5; 2,5.

б) 0,2; 0,5; 1,0; 1,5; 0,8; 1,0; 2,0.

Для параметра a: 1–=0,95; для ²: 1–=0,9.

16.7. Знайти надійний інтервал для математичного сподівання нормального розподілу якщо

16.8. Знайти надійний інтервал для дисперсії нормального розподілу якщо

16.9. За вибіркою з нормального розподілу

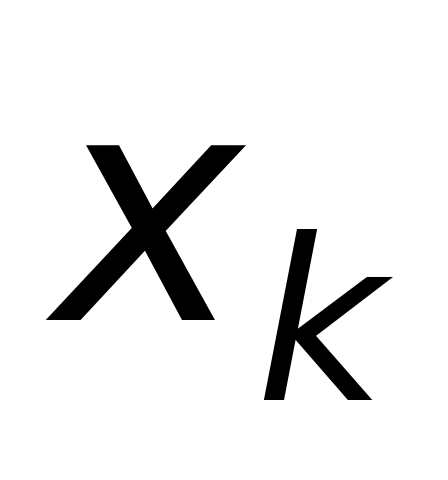
	-2	1	2	3	4	5
	4	3	4	6	2	1

з надійністю 0,95 знайти інтервальні оцінки для параметра a, якщо:

а) ²=4; б)  — невідоме.

Знайти також надійний інтервал для ², якщо:

а) a=2; б) a — невідоме; 1–=0,9.

16.10. Побудувати надійний інтервал для параметра  за вибіркою ₁,₂,…,_n з генеральної сукупності з щільністю

16.11. Для з’ясування використання програмного забезпечення Microsoft у місті довільно

вибрано 100 фірм. Обстеження показало, що 80 фірм використовують програмне

забезпечення. Побудувати 0,95-надійний інтервал для частки фірм, що використовують програмне забезпечення Microsoft у місті.