Розділ 12. Вибірка та її основні характеристики. Емпірична функція розподілу, гістограма
Випадковою
вибіркою об’єму n
(чи вибіркою) називається випадковий
вектор 1,
2,
…, n,
де i
— незалежні і однаково розподілені
Іноді кажуть, що вибірка 1,
2,
…, n
добута з генеральної
сукупності випадкової величини з
функцією розподілу F(x).
Реалізацію вибірки будемо позначати
відповідно X=(x1,
x2,
…, xn).
Розташуємо
величини x1,
x2,
…,xn
у порядку зростання: x(1)x(2)
…x(n),
де
друга
за величиною серед
Позначимо через (k)
випадкову величину, яка для кожної
реалізації X
вибірки
набуває значення x(k),
k=1,2,
…,n.
Отримали нову послідовність випадкових
величин (1),
(2),
…, (n),
які називаються порядковими статистиками.
Причому вони задовольняють нерівність:
Ця послідовність називається варіаційним рядом вибірки.
Позначимо
через n(x)
випадкову величину, рівну числу елементів
вибірки 1,
2,
…, n),
значення яких менші x,
і позначимо,
Функція
називається емпіричною
функцією розподілу. Її
можна використовувати як оцінку функції
Легко бачити, що
— випадкова величина, яка набуває
значення {1;
2;
…;
1}
з імовірністю:
Для кожної реалізації X вибірки функція задовольняє всі властивості функції розподілу: змінюється від 0 до 1, неперервна зліва, неспадна.
Якщо всі компоненти вектора X різні, то
Якщо деякі компоненти вектора X повторюються, то реалізацію вибірки зручніше задавати таблицею (статистичний ряд):
-
Значення
y1
y2
…
ys
Частота
m1
m2
…
ms
,
де y1, y2, …, ys — різні значення даних варіаційного ряду x(1)x(2) …x(n), а mi — кількість повторів значення yi у цьому ряді, i=1, 2, …, s. Легко бачити, що m1+m2+…+ms=n. Тоді
Теорема
Гливенка.
Теорема Колмогорова. Якщо F(x) — неперервна, тоді для будь-якого t>0
Теорема
Колмогорова показує, що оцінка F*n(x)
дає рівномірну оцінку з точністю до
величини порядку
Нехай
тепер
неперервна випадкова величина з щільністю
p(x).
Для оцінки p(x)
з реалізації X=(x1,
x2,
…, xn)
вибірки
розіб’ємо множину значень
на s
інтервалів довжини hi,
i=1,
2,
…, s.
Нехай
–
середина i-го
інтервалу,
– кількість елементів xj,
j=1,
2,
…, n,
які потрапили в i-ий
інтервал. Тоді
–
оцінка щільності в точці
.
Прямокутники з основами hі
і висотами
,
i=1,
2,
…, s
у прямокутній системі координат
називаються гістограмою
вибірки. Якщо на
гістограмі ординати відповідні
послідовно з’єднати відрізками прямих,
то здобута ламана буде
полігоном частот.
Полігон частот є також статистичним
аналогом теоретичної щільності. Для
інтервальних оцінок
.
Приклад розв’язання задачі
Задача 1. Побудувати полігон частот та емпіричну функцію розподілу для вибірки, представленої статистичним рядом:
-
1
4
6
10
25
15
Р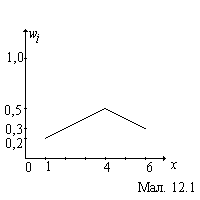
озв’язок.
На малюнку 12.1
зображено полігон частот, а на малюнку
12.2
— емпіричну функцію розподілу.
Задачі
12.1. Записати вибірку 4, 2, 10, 3, 5, 4, 4, 10, 7, 3, 2, 4, 3, 5, 2 у вигляді: а) варіаційного; б) статистичного ряду.
12.2. Побудувати емпіричну функцію розподілу та полігон частот для вибірки, поданої у вигляді таблиці частот:
а)
-
yі
2
5
7
8
mі
1
3
2
8
б)
-
yі
0
1
2
3
4
5
7
mі
8
17
16
10
6
2
1
12.3. Побудувати емпіричну функцію розподілу, гістограму та полігон частот вибірки, поданої у вигляді таблиці частот:
а)
-
Інтервал
[–3;–2)
[–2;–1)
[–1;0)
[0;1)
[1;2)
[2;3)
[3;4)
[4;5)
mі
3
10
15
24
25
13
7
3
б)
-
Інтервал
[0,2;2,2)
[2,2;4,2)
[4,2;6,2)
[6,2;8,2)
[8,2;12,2)
mі
70
20
4
3
3
12.4. Нехай
=(1,
2,
…, n)
— вибірка з рівномірного на відрізку
[a,
b] розподілу. Довести, що сумісна щільність
розподілу (1)
та (n)
має вигляд
Знайти
