Розділ 10. Неперервні випадкові величини

Нехай (, , P) — ймовірнісний простір. Випадковою величиною називається функція (w) на , яка вимірна відносно -алгебри , тобто така функція, коли при кожному дійсному x

Функцією розподілу випадкової величини (w) називається функція

Функція розподілу F(х) має властивості: а) неперервна зліва; б) неcпадна на (–, +); в) F(–) =0, F (+) = 1.

Для кожної функції F (x), що має ці властивості, можна побуду­вати ймовірнісний простір (, , Р) і випадкову величину (w) на ньому, яка має функцією розподілу F(х).

Якщо F (х) — функція розподілу випадкової величини , то

P{ax<b}=F(b)–F(a), (a < b).

Щільність розподілу випадкової величини . Якщо функцію розподілу F(x) випадкової величини  можна подати у вигляді

F(x)=

то кажуть, що випадкова величина  має щільність розподілу p(x), і таку випадкову величину називають неперервною. Майже при всіх x виконується рівність F'(x) = p(x). Щільність розподілу p(x) — невід'ємна функція і

.

Виконується рівність:

P{a<b}= .

Рівномірний розподіл. Випадкова величина  має рівномірний розподіл на відрізку [a, b], якщо

Нормальний розподіл N(a, ²). Випадкова величина має нормальний N(a, ²) розподіл, якщо

.

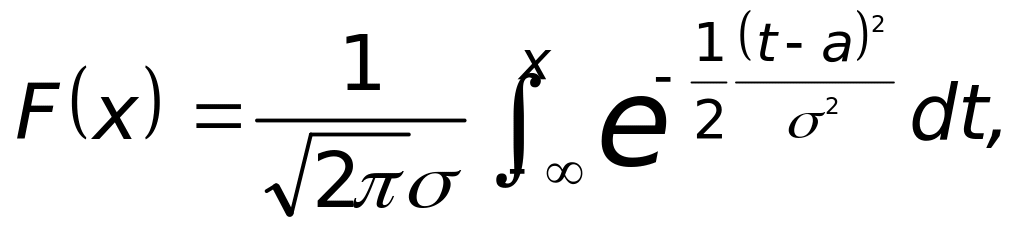
Показниковий розподіл. Випадкова величина  має показниковий розподіл з параметром , якщо

Функція розподілу випадкового вектора (₁, ₂, …, _n) — це ймовірність .

Незалежні випадкові величини. Випадкові величини ₁, ₂, …, _n незалежні, якщо

.

Математичне сподівання випадкової величини. Нехай (w) — випад­кова величина на ймовірнісному просторі (, , P).

Випадкова величина (w) має математичне сподівання, якщо існує інтеграл

Якщо F(x) — функція розподілу , а p(x) — щільність неперервної випадковоі величини, то

де (x) — борелівська функція і

Для математичного сподівання неперервної випадкової величини справджуються всі властивості математичного сподівання дискретної випадкової величини.

Дисперсія випадкової величини. Неперервна випадкова величина (w) має дисперсію

Нерівність Чебишева.

Правило 3. де

Аналогічно дискретним випадковим величинам вводяться коефіцієнти кореляції і коваріації випадкових величин.

Приклад розв’язання задач

Задача 1. Нехай F(x), p(x) — відповідно функція розподілу і щільність випадкової величи­ни . Знайти функцію розподілу і щільність розподілу ви­падкової величини =e^.

Розв’язок. При x0 P{e^<x}=0; при x>0 маємо

F_(x)=P{e^<x}=P{<lnx}=F(lnx).

Отже,

Задача 2. Випадкові величини ₁ та ₂ незалежні рівномірно розподілені на відрізку [0, 1]. Знайти функцію розподілу випадкової величини =₁+₂.

Розв’язок. Функція розподілу випадкових величин ₁ та ₂ має вигляд:

Помітимо, що при та при

Якщо то

а при

Отже,

Задачі

1. Які з поданих нижче функцій є функціями розподілу:

а) F(x)=3/4+(1/2)arctgx?

б) ? в) ?

г) ? д) ?

2. Щільність розподілу випадкової величини  дорівнює p(x)=ae^-|x| (>0). Обчислити: а) коефіцієнт a; б) функ­цію розподілу ; в) M, D; г) побудувати графіки щіль­ності розподілу і функції розподілу.

3. Нижче подано функції, що залежать від певних параметрів. Визначити, при яких значеннях параметрів ці функції будуть щільностями розподілів.

а) б)

4. Нехай F(x) — функція розподілу випадкової величи­ни . Знайти функцію розподілу і щільність розподілу ви­падкової величини =–.

5. Нехай  — випадкова величина, рівномірно розподі­лена на [–1, 1]. Знайти розподіл випадкової величини =||.

6. Випадкова величина  рівномірно розподілена на відрізку [0, 1]. Знайти щільності розподілу випадкових величин: а)  = ²; б)  = 1/ в) =e^ і побудувати графіки їх.

7. Нехай  — випадкова величина з неперервною функцією розподілу F(x) і =F(). Обчислити функцію розподілу .

8. Випадкова величина  має щільність розподілу (розподіл Коші). Обчислити ймовірності: а) б)

9. Випадкова величина  має показниковий розподіл з параметром  Обчислити ймовірності: а) P{ > 3}; б) P{>6/>3}; в) P{ > t+3/>t}.

10. Щільність розподілу випадкової величини  дорівнює: . Знайти розподіл випадкової величини =arctg.

11. Випадкова величина  рівномірно розподілена на відрізку [0, 2]. Знайти функцію розподілу випадкової величини = |– 1|.

12. Випадкова величина  має щільність розподілу . Обчислити щільність розподілу випадкової величини =².

13. Випадкова величина  рівномірно розподілена на відрізку Знайти щільність розподілу випад­кової величини  = sin.

14. Випадкова величина  має розподіл Коші з щіль­ністю . Знайти щільність розподілу випадкової величини

15. Випадкова величина  має показниковий розподіл iз щільністю Знайти функцію розподілу і щільність імовірності випадкової величини

16. Нехай — випадкова величина, яка рівномірно роз­поділена на (0,1). Знайти функцію розподілу випадкової величини  = . Обчислити M.

17. Нехай  — рівномірно розподілена на [0,1] випадко­ва величина. Знайти функцію розподілу випадкової величи­ни  =

18. Нехай  має показниковий розподіл з параметром . Обчислити: M^k, D, P{>1}.

19. Нехай  рівномірно розподілена на [a, b]. Обчислити: M, D.

20. Нехай  нормально розподілена з параметрами (a, ²). Обчислити M, D, M|–a|.

21. Щільність розподілу випадкової величини  дорівнює:

а) знайти сталу a; б) знайти функцію розподілу F(x) і побудувати графіки функцій p(x) та F(x); в) обчислити

22. Щільність розподілу випадкової величини , дорівнює:

а) знайти сталу a; б) знайти функцію розподілу F(x) і побудувати графіки функцій p(x) та F (x).

23. Щільність розподілу випадкової величини  дорівнює:

а) знайти функцію розподілу та побудувати її графік; б) обчислити ймовірність P{–1 <  < 0,5}.

24. Щільність розподілу випадкової величини  дорівнює:

Знайти M, D, обчислити ймовірність того, що відхилення  від математичного сподівання не перевищить 0,5.

25. Знайти математичне сподівання і дисперсію випадкової величини , що має щільність розподілу:

26. Щільність розподілу випадкової величини  дорівнює:

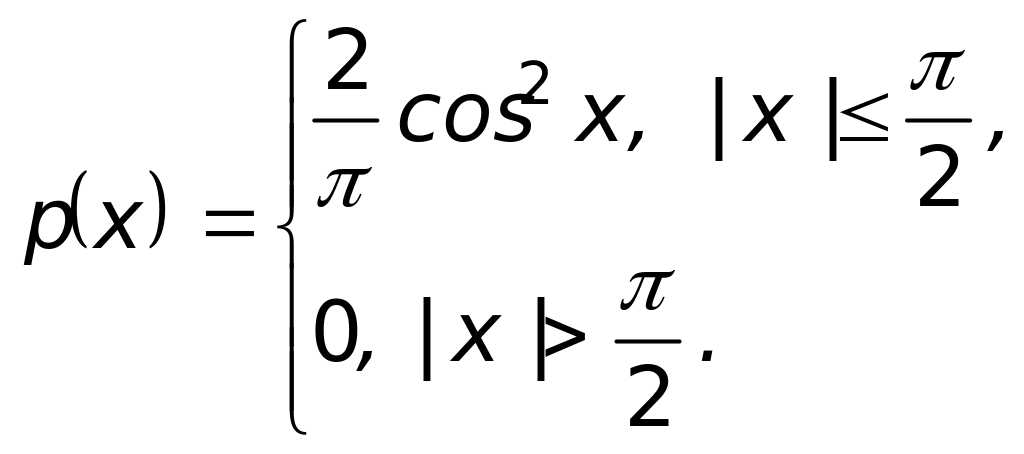
Знайти M, D.

27. Випадкова величина  рівномірно розподілена на [0,1]. Обчислити:

a) б) Ме^.

28. Нехай — випадкова величина з щільністю розподілу Обчислити

29. Нехай M=1, D=0,04. Оцінити ймовірність того, що 0,5<<1,5.

30. Математичне сподівання річної кількості опадів у даній місцевості дорівнює 55 см. 0цінити ймовірність того, що в цій місцевості випаде за рік не менше 175 см опадів.

31. Середнє річне число сонячних днів у даній місцевості дорівнює 75. Оцінити ймовірність того, що протягом року в цій місцевості буде не більше 200 сонячних днів.

32. Нехай ₁ та ₂ — незалежні випадкові величини і =₁+₂. Довести, що: а) б) якщо існують щільності розподілу, то

33. Нехай ₁ та ₂ — незалежні випадкові величини і =₁–₂. Довести, що: а) б) якщо існують щільності розподілу ₁ та ₂, то

34. Нехай ₁ та ₂ — незалежні випадкові величини і =₁₂. Довести, що: а) б) якщо випадкові величини ₁ та ₂ мають щільність розподілу, то

35. Нехай ₁ та ₂ — незалежні випадкові величини і Довести, що: а) б) якщо випадкові величини ₁ та ₂ мають щільність розподілу, то

36. Нехай ₁ та ₂ — незалежні випадкові величини, рівномірно розподілені на Знайти щільність розподілу випадкової величини  = ₁+₂.

37. Випадкові величини ₁ та ₂ незалежні і рівномірно розподілені на відрізку [0,1]. Знайти щільність розподілу випадкових величин: а)  = ₁₂; б) =₁–₂; в) =|₁–₂|.

38. Нехай  і  — незалежні випадкові величини, які мають показниковий розподіл з параметром . Обчислити: а) щільність розподілу – ; б) щільність розподілу |– |.

39. Випадкові величини  та  незалежні, причому Обчислити розподіл добутку .

40. Нехай  і  — незалежні випадкові величини, які мають щільність розподілу

Довести, що випадкова величина  має нормальний розподіл.

41. Випадкові величини  та  нормально розподілені N(0, ²) і незалежні. Довести, що відношення має розподіл Коші.

42. Нехай  і  — незалежні випадкові величини, які мають показниковий розподіл з параметром . Обчислити: а) функцію розподілу б) щільність розподілу в) ма­тематичне сподівання

43. Випадкові величини ₁ та ₂ незалежні і мають нормальні розподіли N(a₁, ₁²) і N(a₂, ₂²). Довести, що випадкова величина =₁ +₂ має нормальний розподіл N(a₁+a₂, ₁²+₂²).

44. Розподіл Ерланга. Нехай {_k, 1kn} — незалежні однаково розподілені за показниковим розподілом з параметром >0 випадкові величини. Довести, що вели­чина S_n = ₁ + ₂ + … + _n має таку щільність розподілу:

45. Розподіл з n степенями свободи. Нехай ви­падкові величини ₁,..., _n незалежні і мають нормальний роз­поділ N(0, l). Довести, що щільність розподілу випадкової величини = дорівнює

46. Нехай ₁,..., _m, ₁, …, _n — незалежні випадкові величини, які мають нормальний розподіл N(0, 1). Знайти щільність розподілу випадкової величини

47. Розподіл Стьюдента. Нехай , ₁, …, _n — незалежні випадкові величини, які мають нормальний розподіл. Довести, що щільність розподілу випадкової величи­ни дорівнює n — число степенів свободи.

48. Знайти щільність розподілу суми ₁+₂, якщо ₁ та ₂ незалежні, ₁ має нормальний розподіл на [0,1], а ₂ рівномірно розподілена на [0,2].

49. Знайти щільність розподілу суми незалежних випадкових величин ₁ та ₂, якщо ₁ має рівномірний розподіл на [–1, 1], a ₂ має показниковий розподіл з параметром .

50. Випадкова величина має рівномірний розподіл на відрізку [–a; a]. Знайти коефіцієнт кореляції між: а)  та ²; б)  та ³.

51. Випадкові величини  та  незалежні і мають однаковий розподіл, M=M=a, D=D=². Знайти

52. Нехай   та  попарно некорельовані випадкові величини. Чи можна стверджувати, що некорельованими будуть випадкові величини: а)  та +? б)  та ?