2.2. Минимизация фал методом Квайна-Мак-Класски.
Данный метод основывается на задании входящих в ДСНФ функции элементарных произведений в виде двоичных чисел, называемых номерами соответствующих наборов. Кроме номера каждому произведению присваивается определенный индекс, под которым понимается число единиц в двоичном представлении данного набора. Например:
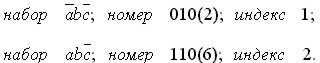
В результате реализации данного метода ФАЛ разлагается на простые импликанты. Под простой импликантой функции понимается всякое элементарное произведение, принимающее единичное значение на всех наборах аргументов, что и исходная ФАЛ, при исключении из которого хотя бы одного аргумента, уже не будет выполнятся данное условие.
Алгоритм Квайна-Мак-Класски формулируется следующим образом: для того, чтобы два числа m и n являлись номерами двух склеивающихся между собой наборов, необходимо и достаточно, чтобы индексы данных чисел отличались на единицу, сами числа отличались на степень числа два и число с большим индексом было больше числа с меньшим индексом.
Реализацию алгоритма рассмотрим на примере минимизации ФАЛ
На первом этапе минимизации определяем номера и индексы каждого набора, записывая ФАЛ в виде
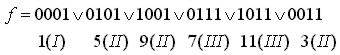
Группируем наборы располагая их в порядке возрастания индексов
Минимизация ФАЛ методом Квайна-Мак-Класски.
На следующем этапе производим склеивание различных наборов, руководствуясь приведенной выше формулировкой алгоритма. Подлежащие склеиванию пары чисел указаны стрелками. При склеивании не совпадающие в числах разряды отмечаются прочерками. Например склеивание чисел 0001 и 0011 дает число 00-1. Результат склеивания выписывается в следующий столбец таблицы 2.1., так же разделяемый на строки с индексами, отличающимися на единицу. После склеивания всех групп первого столбца таблицы переходят ко второму столбцу, вписывая результат склеивания в третий столбец. При объединении наборов второго и последующих столбцов таблицы, возможно склевать только числа содержащие прочерки в одноименных разрядах. Склеивание продолжается до тех пор, пока образование нового столбца станет невозможным.
По окончании склеивания приступают к построению импликантной таблицы (см. табл. 2.2.), записывая в нее в качестве простых импликант наборы, содержащиеся в последнем столбце табл. 2.1. В качестве простых импликант в табл. 2.2. так же вписываются наборы из других столбцов табл. 2.1. не принимавшие участия в склеивании. Если импликанта, содержащаяся в I-той строке таблицы, составляет некоторую часть конституенты I-го столбца на пересечении I-той строки и I-го столбца ставится символ *. С целью получения минимальной формы ФАЛ из табл. 2.2. необходимо выбрать минимальное число строк, чтобы для каждого столбца, среди выбранных строк нашлась хотя бы одна, содержащая в этом столбце символ *.
Импликантная таблица минимизируемой ФАЛ.
Полученная после минимизации ФАЛ записывается в следующем виде:
2.3 Синтез логических устройств в заданном базисе
Применение теорем Де Моргана
Двойное инвертирование для применения терем Де Моргана
Синтезированная функция может содержать только заданный элемент и инвертор.
Например, задана функция, привести её к заданному базису:
На практике обычно задается базисный элемент и количество входов, например, 2И-НЕ, или 5ИЛИ-НЕ. Здесь может быть несколько вариантов:
Число входов равно количеству переменных
Число входов больше количества переменных
Число входов меньше количества переменных
Рассмотрим второй и третий случаи
2. Лишние входы необходимо изолировать, рассмотрим обобщенную таблицу истинности:
х1 |
х0 |
х1 х0 |
х1 + х0 |
х1|х0 |
х1↓х0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
Для штриха Шеффера, «0» на входе однозначно определяет «1» на выходе, а для стрелки Пирса «1» на входе однозначно определяет «0» на выходе, следовательно:
Штрих Шеффера: «0» - активный логический уровень, «1» - пассивный.
Стрелка Пирса: «1» - активный логический уровень, «0» - пассивный
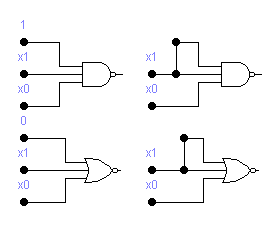
Следовательно для изоляции лишних выводов можно идти следующими путями:
На лишние выводы подавать пассивные логические уровни.
на несколько входов подавать один и тот же логический уровень, согласно правилу «х+х+…+х=х»
2. Если число входов больше заданного, то необходимо сократить количество переменных, здесь опять возможны два случая, когда члены исходной ФАЛ содержат общие элементы и есть возможность вынести их за скобку. И второй, когда не содержат и тогда необходимо применять специальное правило. Рассмотрим подробнее оба случая.
Первый:
Второй,
применяем следующее правило:
для
примера рассмотрим формулу (24.1)
