1.2. Способы задания фал.
Для описания ФАЛ используют различные способы. Обычно применяют их последовательно для получения ФАЛ.
Описание функции в словесной форме
Описание функции в виде таблиц истинности
Описание функции в виде алгебраического выражения
Запись в виде последовательности десятичных чисел
кубические комплексы
1. Словесное описание ФАЛ
Некоторое устройство, имеющее три контакта на входе, срабатывает в том случае, когда на любых двух контактах одновременно присутствует напряжение, определяющее логическую единицу.
2. Описание ФАЛ в виде таблицы истинности. Таблица, содержащая все возможные комбинации входных переменных и соответствующие им значения выходных переменных называется таблицей истинности или комбинационной таблицей. Таблица содержит (п+1) столбец, где п – количество входных переменных и (2п+1) строк. Для некоторого заданного словесного описания таблица будет выглядеть следующим образом
-
х2
х1
х0
у
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
1
1
1
0
1
1
1
1
1
3. Описание функции в виде алгебраического выражения. Для этого используются две стандартные формы её представления.
1. Дизъюнктивная нормальная форма ДНФ
2. Конъюнктивная нормальная форма КНФ
дизъюнктивная нормальная форма
1). Находим конституанты единицы, т. е. для значений выходной переменной равной единице записываем логические произведения соответствующих входных переменных, причем значения входных переменных равные нулю записываются с инверсией.
2). Записываем логические суммы полученных конституент единицы.
В
итоге получаем:
конъюнктивная нормальная форма
1). Находим конституанты нуля, т. е. для значений выходной переменной равной нулю записываем логические суммы соответствующих входных переменных, причем значения входных переменных равные единице записываются с инверсией.
2). Записываем логические произведения полученных конституант нуля
В
итоге получаем:
По полученным ФАЛ можно построить логическую схему.
получится следующая схема (рис.2).
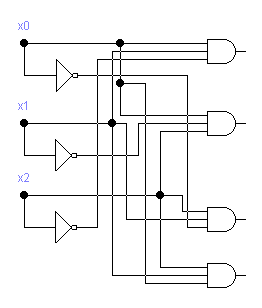
Последовательность десятичных чисел
Последовательно записываются десятичные эквиваленты кодов соответствующих конституант нуля или единицы, знак «Σ» используется для ДНФ, знак «П» для КНФ, в нашем примере:
Σ((0,1,1);(1,0,1);(1,1,0),(1,1,1))= Σ(3,5,6,7)
П((0,0,0);(0,0,1);(0,1,0);(1,0,0))=П(0,1,2,4)
кубические комплексы
строятся для количества переменных не более трех, то есть строится куб, его вершины обозначаются всеми наборами переменных, а существующие в заданной задаче наборы выделяются.
В нашем примере
