- •Электроника
- •Руководство и задания на выполнение расчетно-графической работы
- •Расчет вторичного источника питания
- •1. Требования к содержанию и оформлению ргр
- •1.1 Задание на ргр
- •1.2 Оформление ргр
- •1.3 Структура расчетно-пояснительной записки
- •2. Методические указания к выполнению работы
- •2.1 Общие сведения об источниках питания
- •Структурная схема источника питания
- •2.2. Расчет стабилизатора на интегральной микросхеме
- •Расчетная схема стабилизатора на микросхеме серии кр142
- •Параметры микросхем серии кр 142
- •2.3. Расчет стабилизатора с усилителем тока на транзисторе
- •2.4. Расчет емкостного фильтра
- •2.5. Расчет выпрямителя
- •2.5.1 Однополупериодный выпрямитель
- •2.5.1.1 Расчет выпрямителя
- •2.5.1.2. Расчет трансформатора
- •2.5.2 Двухполупериодный выпрямитель со средней точкой трансформатора
- •2.5.2.1 Расчет выпрямителя
- •2.5.1.2. Расчет трансформатора
- •2.5.3 Однофазный мостовой выпрямитель (схема Гретца)
- •2.5.3.2. Расчет трансформатора
- •2.5.4 Однофазный мостовой выпрямитель с удвоением напряжения (схема Латура)
- •2.6 Выбор деталей выпрямителей
- •2.7. Расчет параметров трансформатора или выбор стандартного
- •2.7.1 Упрощенный расчет однофазных трансформаторов
- •2.8. Расчет коэффициента полезного действия
- •2.9. Составление принципиальной электрической схемы
- •Ворпросы к защите ргр
- •Рекомендуемая литература
- •Параметры полупроводниковых стабилитронов
- •Параметры транзисторов
- •Стандартные ряды сопротивлений резисторов
- •Параметры полупроводниковых диодов
- •Параметры полупроводниковых диодных сборок (мостовой выпрямитель)
- •Конденсаторы с оксидным диэлектриком
- •Задание
- •Теоретические сведения для выполнения ргр
- •Пример выполнения работы Введение
- •Варианты заданий
- •Список рекомендованной литературы
- •Расчетно-графическая работа по цифровой электронике Анализ и синтез дискретных устройств
- •Теоретическое введение
- •1.1 Реализация функций алгебры логики на контактных реле и бесконтактных логических элементах
- •1.2. Способы задания фал.
- •1.3. Формы представления фал
- •1.4. Основные законы и тождества алгебры логики
- •2.1. Минимизация фал методом карт Карно
- •2.2. Минимизация фал методом Квайна-Мак-Класски.
- •2.3 Синтез логических устройств в заданном базисе
- •2.4. Синтез различных комбинационных схем
Расчетно-графическая работа по цифровой электронике Анализ и синтез дискретных устройств
В кратком изложении содержатся основные сведения о формах предоставления, способах задания реализации функций алгебры логики на основе контактных и бесконтактных элементов. Без доказательств приведены основные законы и тождества алгебры логики.
На конкретных примерах рассматриваются, используемые в инженерной практике, методы минимизации функций, основанные на применении законов и тождеств алгебры логики, карт Карно и Алгоритма Квайна-Мак-Класски.
Описываются методы логического проектирования комбинационных схем. По каждому разделу излагаемого материала приведены варианты заданий для выполняемой студентами контрольной работы и список рекомендуемой литературы.
Предназначено для выполнения расчетно-графической работы по дисциплине «Электроника».
Теоретическое введение
1.1 Реализация функций алгебры логики на контактных реле и бесконтактных логических элементах
Функции и аргументы в алгебре логики (АЛ) определены на множестве {0, 1} и следовательно, могу принимать только два значения. Истинному значению ставится в соответствие символ «1», а ложному «0». Как и в обычной алгебре функции и аргументы в АЛ обозначаются буквами выбранного алфавита. Различные комбинации значений аргументов называются наборами. Для каждого набора аргументов можно задать два значения ФАЛ, следовательно для n аргументов можно получить (2)n различных функций. С целью получения новых функций можно использовать принцип суперпозиции, позволяющий подставлять одни функции вместо аргументов в другие функции. Система ФАЛ позволяющая получать любые, сколь угодно сложные функции называется функционально полной системой, а набор элементов реализующих данные функции – функционально полным набором или базисом. При построении дискретных устройств наибольшее распространение получили, функции реализующие операции, представленные в табл. 1.1.
Таблица 1.1.
Реализация и обозначение основных логических функций.
Дизъюнкция, Логическое сложение или она еще называется функция –ИЛИ– реализует функцию логического сложения.
Это функция n-переменных, принимает значение логической единицы, когда хотя бы одна из переменных равна единице, обозначается знаками: + и ν
х1 |
х0 |
х1+х0(х1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
Условное обозначение:
Отечественное международное


f
Логическое умножение. Функция – И, n-переменных, реализует функцию логического умножения. Уровень логической 1 на его выходе появляется только в том случае, если на оба его входа подается уровень логической единицы (табл. 2). Эта операция справедлива тоже для произвольного количества переменных. Она соответствует математической операции пересечения множеств. Число переменных также обозначается цифрой. В приведенном примере выполняется операция 2И. Математически она соответствует операции пересечения множеств.
х1 |
х0 |
х1х0(х1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Условное обозначение:
о течественное
международное
течественное
международное


Логическое
отрицание.
Функция – НЕ или инвертор. Изменяет
состояние входного сигнала на
противоположное. Для её обозначения
используют черту над соответствующим
выражением. Операция определяется
следующими постулатами:
![]() Инвертор производит действие только
над одной переменной.
Инвертор производит действие только
над одной переменной.
У словное
обозначение:
словное
обозначение:
О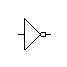 течественное
международное
течественное
международное
Стрелка Пирса или функция ИЛИ-НЕ: это операция отрицания логической суммы
Условное
обозначение
![]()
Международное отечественное

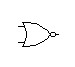
Штрих Шеффера или функция И-НЕ: это операция отрицания логического произведения
Условное обозначение: x1|x0
отечественное международное

![]()
Используя эти элементы можно получить любую из основных логических функций
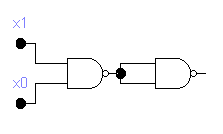
На элементе И-НЕ
Н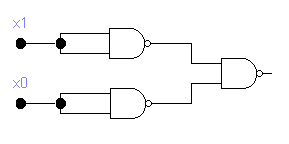 Е
ИЛИ
И
Е
ИЛИ
И
![]()
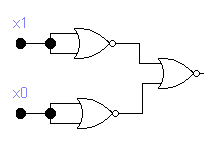
На элементе ИЛИ-НЕ
НЕ ИЛИ И