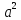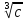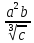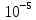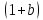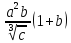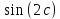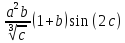Численные методы / Курсовая работа по ЧМ вариант 39
.docxМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Курсовая работа
по дисциплине «Численные методы»
Вариант № 39
Выполнил:
Студент Ермилин М.В.
Группа ФБИ-91
Факультет Бизнеса
Шифр 090309304
Преподаватель: Соболева О.Н.
Дата сдачи
Дата защиты
Новосибирск, 2012
Курсовое задание
Вариант 39
Задание 1. Запишите порядок выполняемых вами операций, оцените погрешности их результатов, вычислите и запишите искомое значение. Определите число верных знаков.
Задание 2. Выясните погрешность задания исходных данных, необходимую для получения результата с m верными значащими цифрами
1.
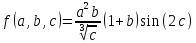
a=0.2456±0.0005; b=0.00078±0.00003; c=0.008±0.004
2.m=4 a=0.2456; b=0.00078; c=0.008
Если трансцендентные функции (sin,ln и т.п.) вычисляются с помощью
библиотек компьютерных средств (Pascal, Delphi, MatLab и пр.) или
калькулятора, погрешность метода можно пренебречь (но не погрешностью
исходных данных или округления).
Задание 3
Исследование метода Холецкого для нахождения собственных значений для
произвольной самосопряженной матрицы.
Для вычислений подберите тесты с известными собственными значениями. Погрешность нужно оценивать по любой норме разности между точными и вычисленными значениями. Симметричные матрицы подбирать разного вида: хорошо и плохо обусловленные, разной размерности, плотные и разреженные.
Задание 1.
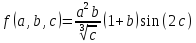
a=0.2456±0.0005; b=0.00078±0.00003; c=0.008±0.004
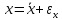
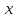 -
точное значение
-
точное значение
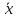 -
приближенное значение
-
приближенное значение
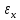 -абсолютная
погрешность
-абсолютная
погрешность
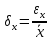 -
относительная погрешность
-
относительная погрешность
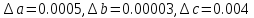
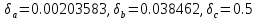
Операции
|
|
2*0.00203583=0.00407166 |
0.00407*0.2456^2=2.456* |
|
|
0.04253 |
2.00115* |
|
|
0.16667 |
0.03333 |
|
|
0.2092 |
4.92133* |
|
|
3* |
22.99766* |
|
|
0.20923 |
4.92588* |
|
|
7.99898* |
0.49996 |
|
|
0.70919 |
2.6713* |
Воспользуемся универсальными оценками:
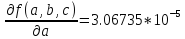
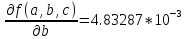
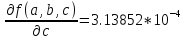
Предельная абсолютная погрешность:
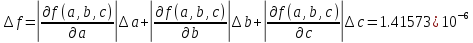
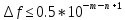
m - число верных знаков
n – старший разряд приближенного значения
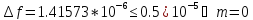
Задание 2.
m=4 a=0.2456; b=0.00078; c=0.008
f(a,b,c)=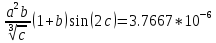
Пологаем верными 4 цифры, тогда
Относительная
погрешность
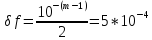
Абсолютная
погрешность
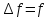 *
*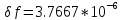 *
*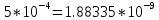
Принцип равных вливаний
a*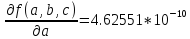
b*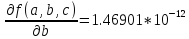
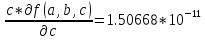
a*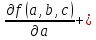 b*
b*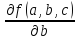 +
+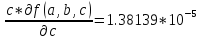
Допустимая погрешность данных
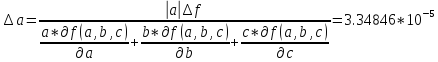
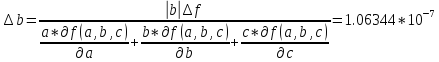
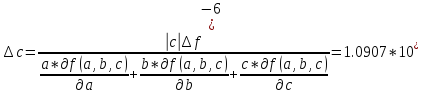
Задание 3
Исследование метода Холецкого для нахождения собственных значений для
произвольной самосопряженной матрицы.
Для вычислений подберите тесты с известными собственными значениями. Погрешность нужно оценивать по любой норме разности между точными и вычисленными значениями. Симметричные матрицы подбирать разного вида: хорошо и плохо обусловленные, разной размерности, плотные и разреженные.
Пусть А-симметричная,
положительная матрица. Тогда она
представима в видеA=L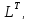 где:
где:
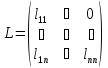 ,
,
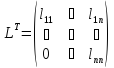
Элементы матрицы L можно вычислить, начиная с верхнего левого угла по формулам:
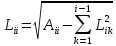
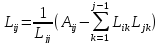
Выражение под корнем всегда >0, если А-действительная положительная матрица.
Существует обобщение этого разложения на случай комплекснозначных матриц. Если А-положительно-определенная эрмитовая матрица, то существует разложение, где L-нижняя треугольная матрица с положительными действительными элементами на диагонали, а L*-эрмитово-сопряженная к ней матрица.
Для комплекснозначных эрмитовых матриц используются формулы:
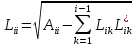
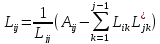
Нахождение собственные значений в MATLAB
Функция holec реализует разложение Холецкого.
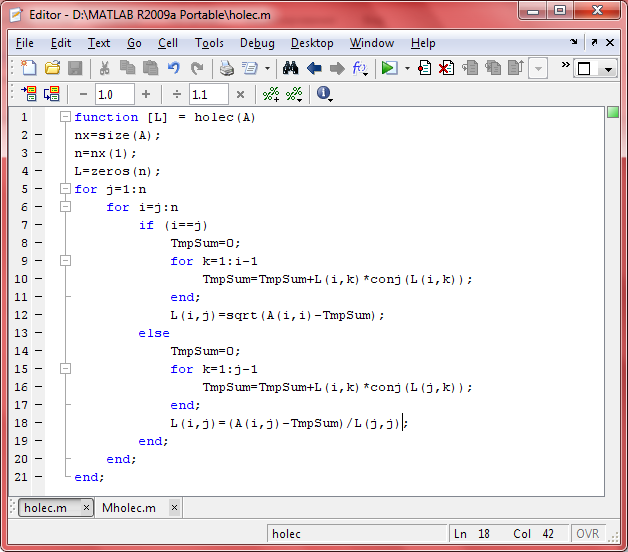
Пример:
Действительная матрица
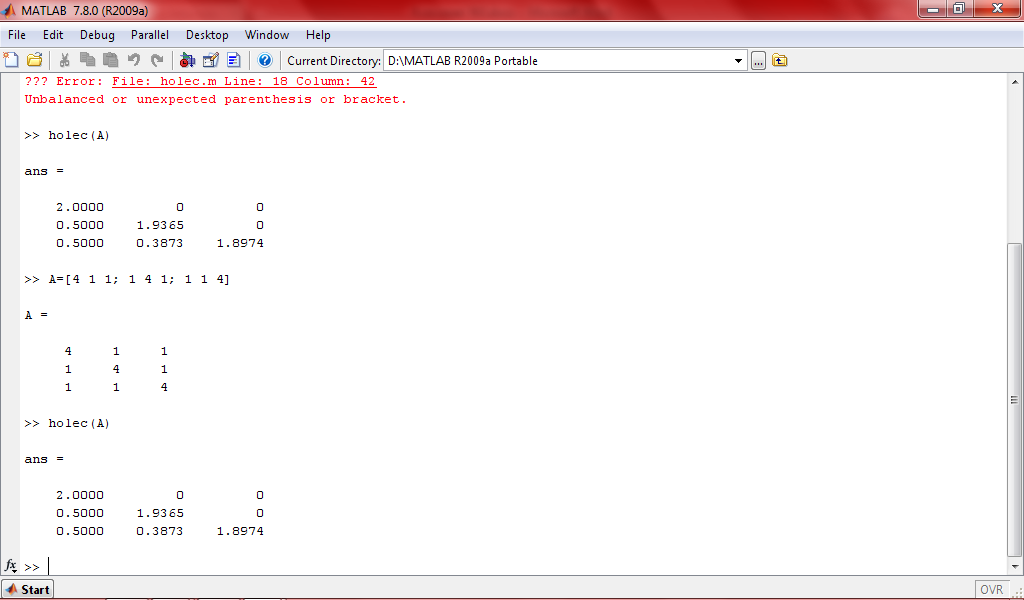
Комплекснозначная матрица
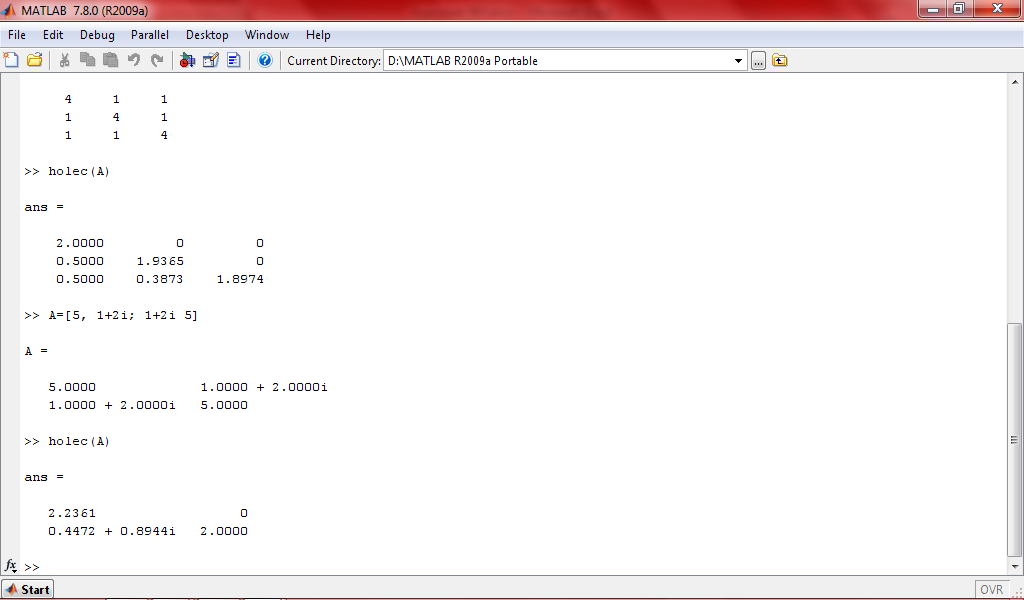
Головная программа. Функция для нохождения собственных значений методом Холецкого.
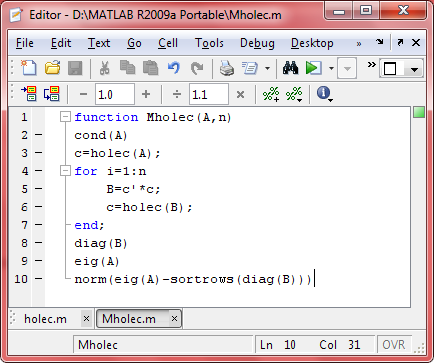
Cond(A)-проверка кондиции А
Diag(B)-вывод диагонали матрицы В
Eig(A)-вывод реальных собственных значений А
Norm(eig(A)-diag(B))-вычисление разности собственных значений матрицы А, вычисленных с помощью стандартной функции eig и нашей программой
Пример:
По степени обусловленности
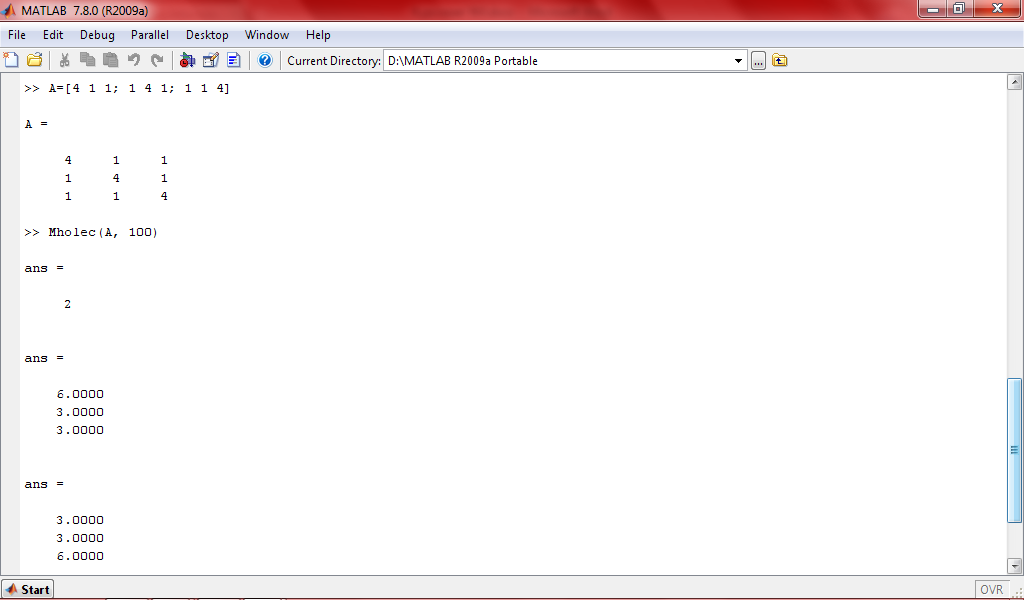
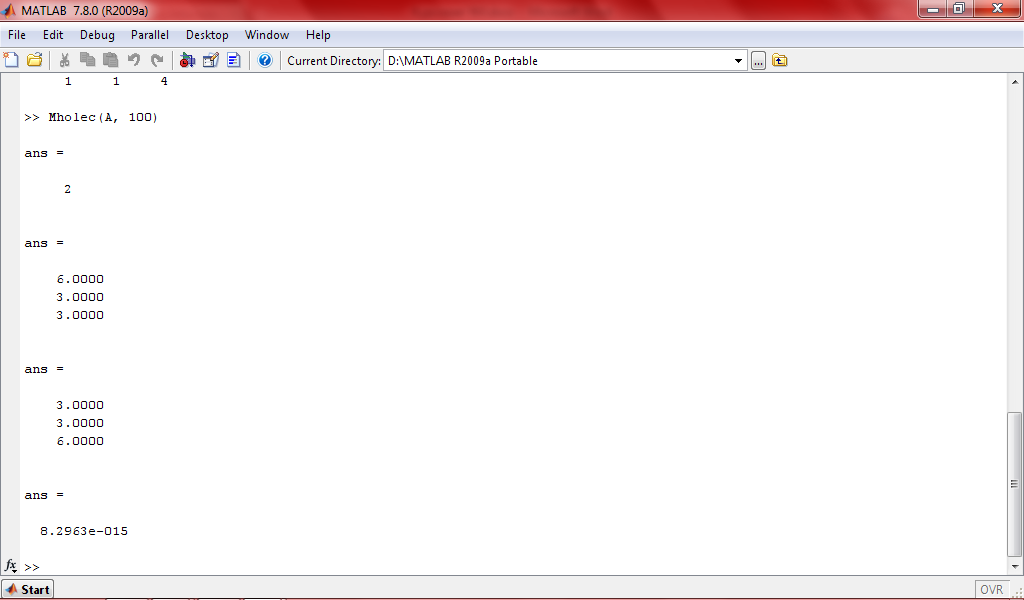
Число обусловленности 2-хорошо обусловленная матрица
Точность вычисления
8.2963*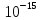
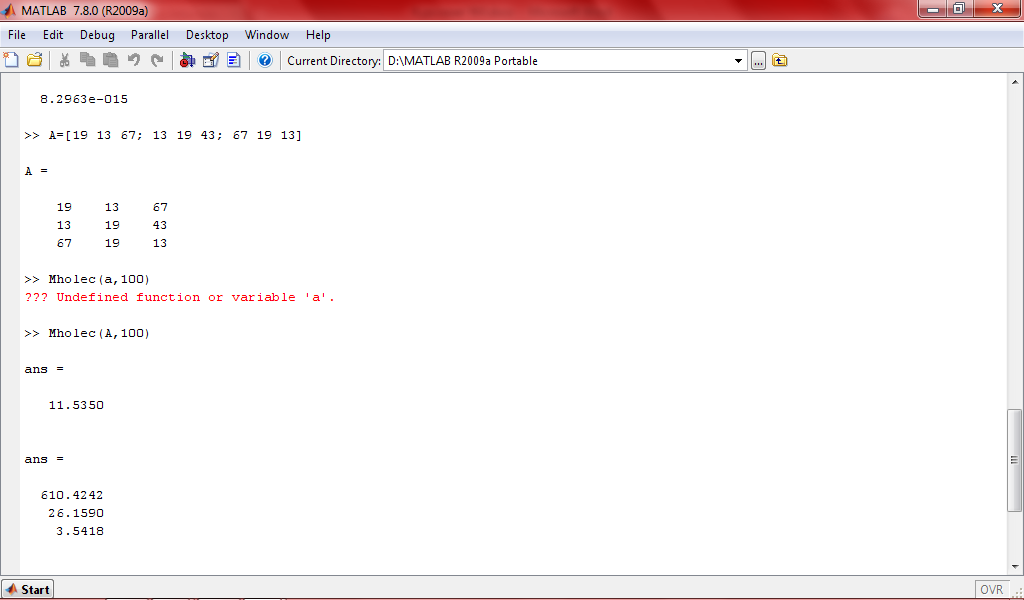
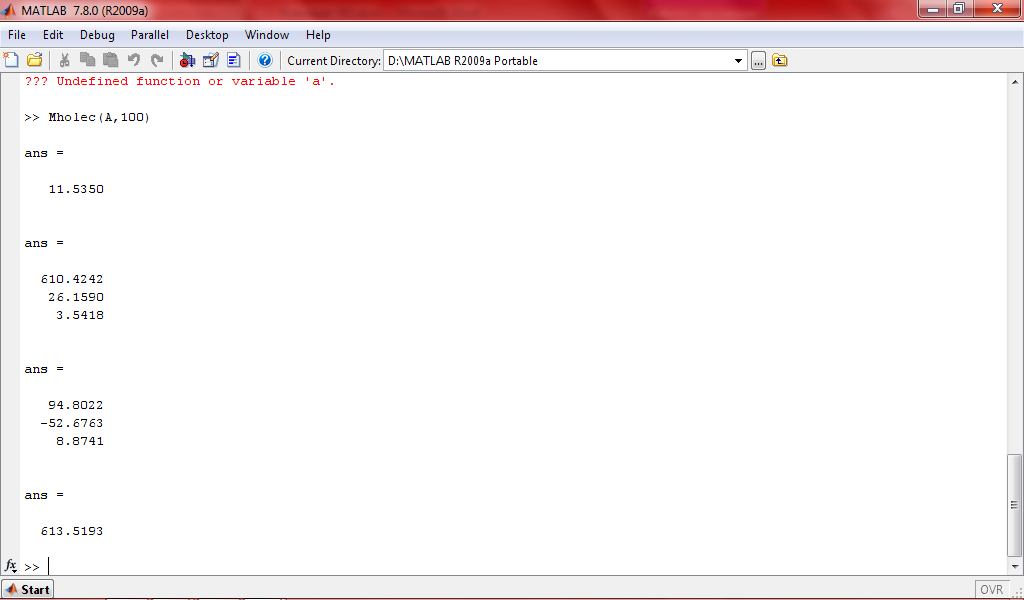
Число обусловленности 11.53-плохо обусловленная матрица
Точность вычислений – 613.519
Вывод: Метод хорошо себя проявляет на хорошо обусловленных матрицах.
По размерности
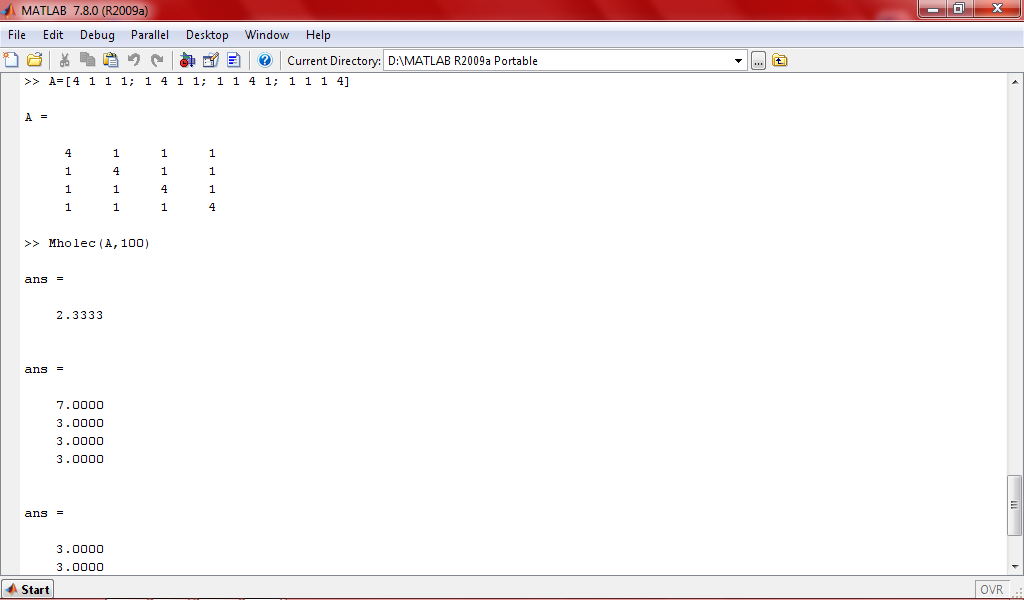
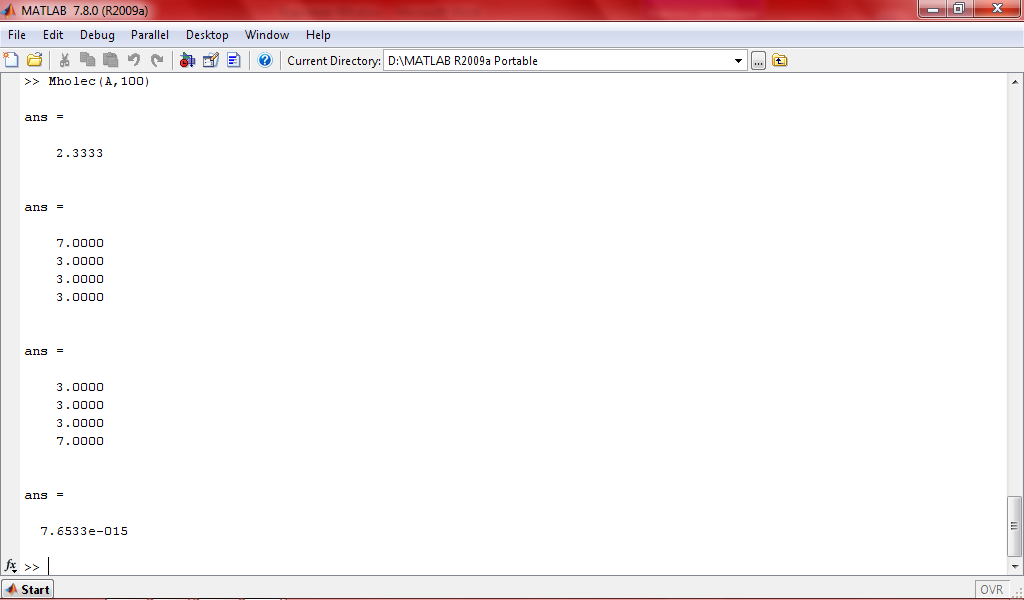
Точность вычислений
– 7.6533*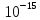
Вывод: С увеличением размерности, точность вычислений увеличивается.
Плотная матрица
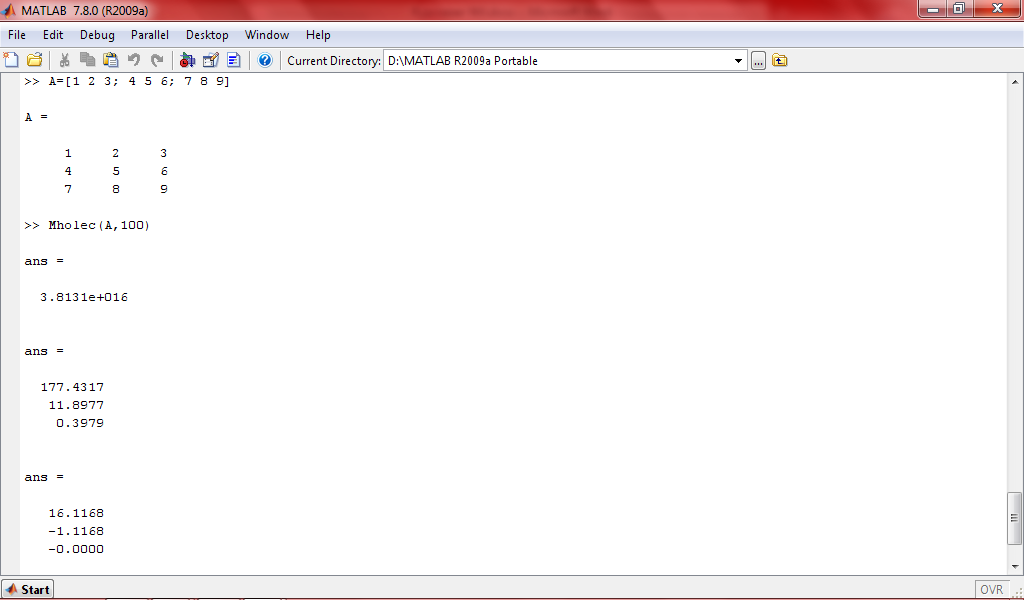
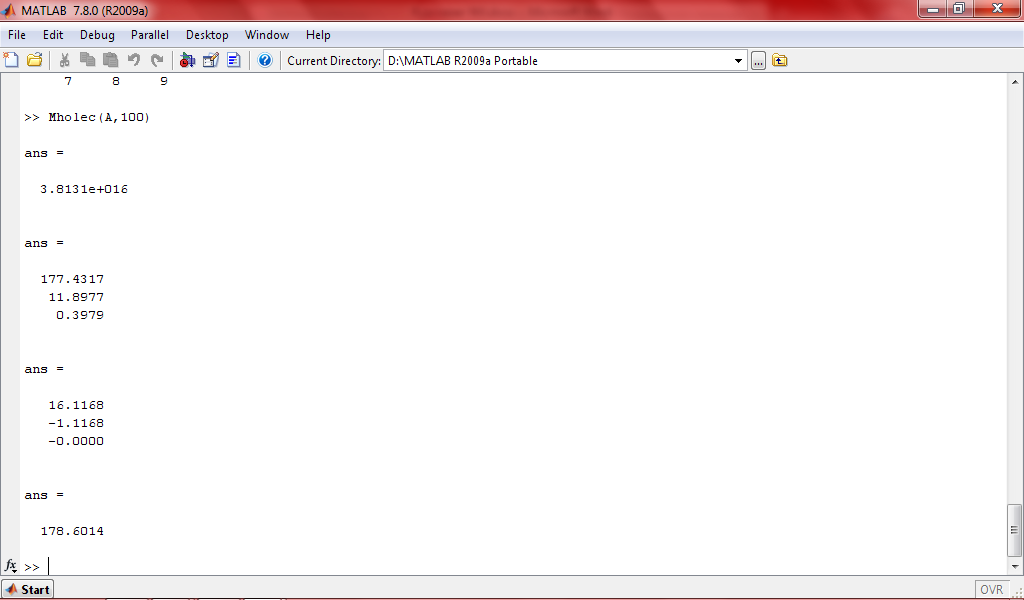
Точность вычислений 178.6
Разреженая матрица
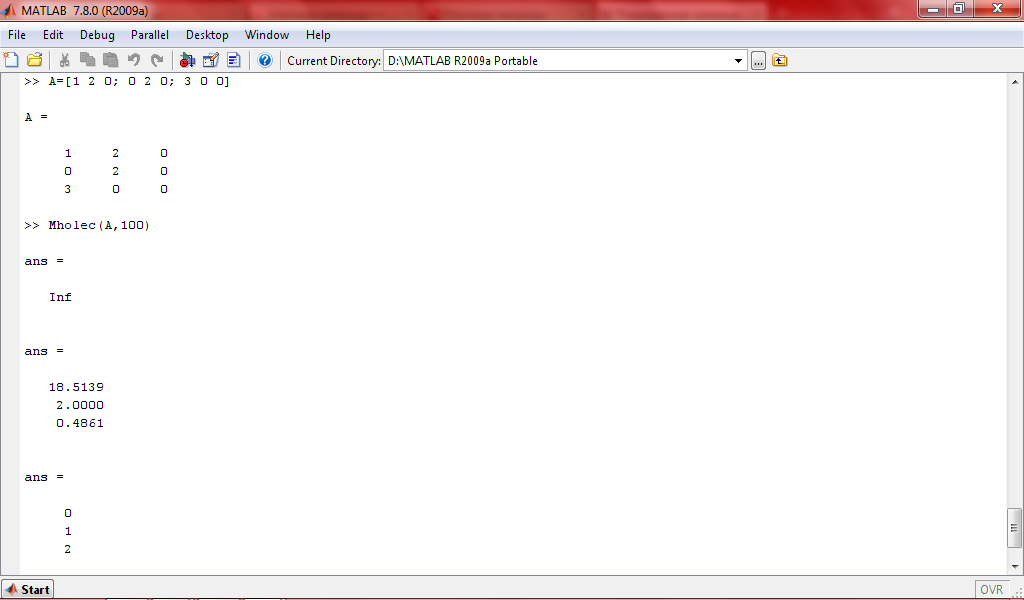
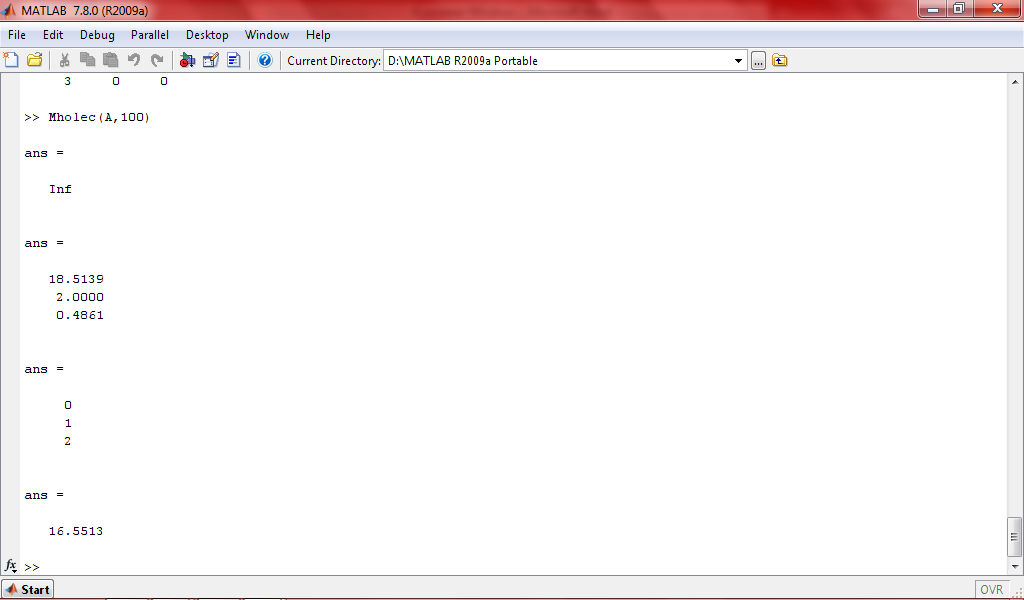
Точность вычислений – 16.55
Вывод: точность вычислений по методы Холечкого разреженых матриц выше, чем плотных.