Лабораторна робота n61. Вивчення законів теплового випромінювання.

(проф. Стаднік Б.М., доц. Холод В.П.)

Мета роботи: вивчення основних закономірностей теплового випромінювання і визначення сталої Стефана-Больцмана.

Теоретичні відомості.

Випромінювання тілами електромагнітних хвиль, що здійснюється за рахунок перетворення внутрішньої енергії тіла в енергію випромінювання, називається тепловим (або температурним) випромінюванням. Теплове випромінювання відбувається за будь-якої температури, але при звичайних температурах випромінюються здебільшого інфрачервоні хвилі, які не викликають зорового відчуття. Інтенсивність теплового випромінювання зростає із збільшенням температури. Тому цей вид випромінювання може перебувати у стані термодинамічної рівноваги з випромінюючими тілами. Розглянувши адіабатичну систему, в якій відбувається обмін енергією через випромінювання, можна впевнитися, що порушення термодинамічної рівноваги в такій системі суперечить другому закону термодинаміки. Тому теплове випромінювання є рівноважним.. Приведемо основні визначення.

Інтегральна енергетична світимість тіла це енергія, що випромінюється з одиниці площі тіла за одну секунду всіма довжинами хвиль. Енергетична світимість тіла є функцією температури і вимірюється у .

Спектральна випромінювальна здатність тіла є потік енергії, що випромінюється одиницею площі поверхні тіла при температурі в інтервалі довжин хвиль , дорівнює В малому інтервалі величину можна вважати пропорційною ширині інтервалу довжин хвиль :

(61.1)

Коефіцієнт пропорційності , що залежить від довжини хвилі і температури, і називається спектральною випромінювальною здатністю тіла є функцією розподілу енергії в спектрі тепло­вого випромінювання тіла. Розмірність є Вт/м³ . Енергетична світимість зв'язана з випромінювальною здатністю співвідношенням:

(61.2)

Спектральна поглинальна здатність тіла. Нехай на елементарну площу поверхні тіла при температурі Т падає потік електромагнітної енергії , причому довжини хвиль випромінювання лежать у вузькому спектральному інтервалі . Частина цього потоку буде поглинатися тілом, а решта відбивається поверхнею і проходити через тіло. Безрозмірна величина:

(61.3)

називається поглинальною здатністю тіла. Вона є функцією довжини хвилі і температури. Поглинальна здатність тіла показує, яка частка енергії електромагнітних хвиль ( в інтервалі від до ), що падає на одиницю поверхні тіла за одиницю часу, поглинається тілом.

Закон Кірхгофа: відношення випромінювально•здатності тіла до його поглинальної здатності не залежить від природи тіла і є універсальною функцією довжини хвилі і температури:

(61.4)

де функція Кірхгофа.

Абсолютно чорним називається тіло, яке здатне при будь-якій температурі поглинати повністю випромінювання будь-якої довжини хвилі, що падає на нього, тобто це є тіло, поглинальна здатність якого . Абсолютно чорних тіл у природі немає, однак такі тіла, як сажа, чорний оксамит і деякі інші у певному інтервалі довжин хвиль за свої ми властивостями близькі до абсолютно чорного тіла. Для абсолютно чорного тіла, відповідно до (61.4) маємо: , тобто знаходження виду функції Кірхгофа зводиться до визначення випромінювальної здатності (закону випромінювання) абсолютно чорного тіла. При вирішенні ції задачі класична фізика натрапила на нездоланні труднощі. Намагаючись пояснити закони температурного випромінювання абсолютно чорного тіла, Релей і Джінс в 1895 р. запропонували наступну формулу, що описує залежність його спектраль­ної густини енергії Е_ν,Т від температури Т

, (61.5)

де ν – частота світла, к – постійна Больцмана, с- швидкість світла.

Як вияснилось, формула Релея-Джінса добре відповідала експериментальним даним лише для малих частот випромінювання. Як показує аналіз формули (61.5), для високих частот (малих довжин хвиль) енергетична світимість абсолютно чорного тіла Е_Т прямує до безмежності, що є ці­лковитим абсурдом, бо це суперечить закону збереження енергії.

Раніше, в 1896 році, Він запропонував формулу для розрахунку спектральної густини ене­ргії в спектрі абсолютно чорного тіла, яка добре зіставляється з експериментальними даними лише в короткохвильовій ділянці спектра, тобто, в тій його частині, де “не працює” формула Релея – Джінса

(61.6)

Таким чином, в кінці ХIX століття було отримано дві формули, які відповідали експериме­нту в обмежених ділянках спектра, але ні одна з них не могла описати всю експериментальну криву залежності спектральної густини енергії абсолютно чорного тіла від температури.

В 1900 році М.Планку вдалося найти, спочатку чисто емпірично, формулу, яка добре відпо­відала результатам досліду як для довгохвильової, так для короткохвильової ділянок спектру ви­промінювання абсолютно чорного тіла переходила відповідно в формулу Релея – Джінса і в фор­мулу Віна

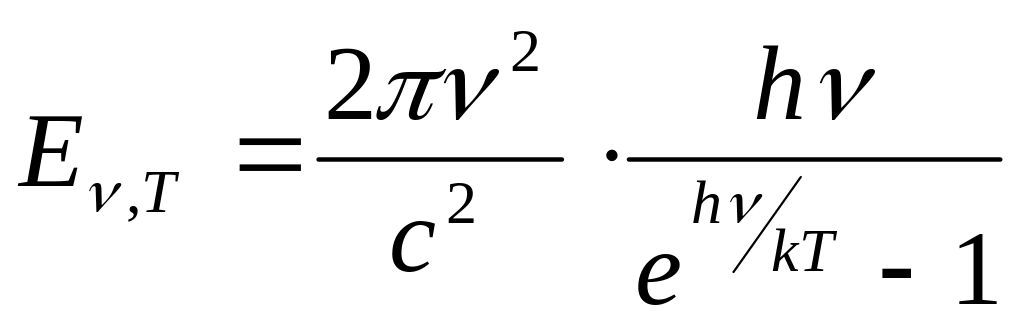(61.7)

Як виявилось, формула Планка є фактично результатом інтерполяції формул Релея-Джінса і Віна. Для виводу формули Планка необхідно було сформулювати гіпотезу, яка явно суперечила уявленням класичної фізики – гіпотезу про те, що енергія макроскопічних систем може приймати лише визначені, дискретні значення. Це змусило Планка при виводі своєї формули схематично уявити випромінюючі матеріальні центри як лінійні гармонічні осцилятори, що несуть електрич­ний заряд, завдяки якому вони можуть обмінюватися енергією з оточуючим електромагнітним по­лем. Гіпотеза, яку заклав в основу виводу своєї формули Планка, така: осцилятори можуть зна­ходитись тільки в станах, в яких їх енергія є кратною до свого найменшого значення. При ви­промінюванні або поглинанні енергії осцилятори переходять із одного стану в інший стриб­ком, минаючи проміжні стани.

В 1913 році Н.Бор дав більш точне формулювання гіпотези Планка і узагальнив її на будь які атомні системи, тобто ним вперше було показано неможливість застосування класичної фізики до внутрішньоатомних процесів. При цьому ідея Планка про кванти, що була застосована для по­яснення процесу обміну енергією між електромагнітним полем і лінійним осцилятором, набула універсального характеру як вираз найбільш характерної особливості процесів внутрішньоатом­ного світу.

Функція Планка добре узгоджується з експериментальними даними в усьому інтервалі довжин хвиль при будь-яких температурах. Для великих довжин хвиль (коли << ) маємо: і формула (61.5) перетворюється на формулу Релєя-Джинса. Для малих довжин хвиль (тобто, коли >> ) і формула Планка перетворюється в формулу Віна.

З формули Планка випливають закони, які були встановлені раніше експериментально встановлені для випромінювання абсолютно чорного тіла.

Закон Стефана-Больцмана. Енергетична світимість абсолютно чорного тіла (в усьому інтервалі довжин хвиль) з 1м² поверхні за 1с пропорційна четвертому степеню його температури:

(61.8)

де - стала Стефана-Больцмана.

Закон "зміщення" Віна. Відшукавши екстремум функції при сталій температурі, одержимо:

(61.9)

де довжина хвилі, що відповідає максимуму випромінювання абсолютно чорного тіла; стала Віна.

Згідно з законом Віна, при зменшенні температури "зміщуються" в напрямку зростаючих .

Сірі тіла. Якщо тіло не є чорним, < 1, то, відповідно, < . Тому випромінювання не чорних тіл відрізняється від випромінювання абсолютно чорного тіла. Існують сірі тіла, для яких має однакове значення для всіх довжин хвиль і залежить лише від тем­ператури, тобто, . В цьому випадку:

(61.10)

де ступінь чорноти (поглинальна здатність сірого тіла при фіксованій температурі).

У даній роботі досліджується залежність потужності теплового випромінювання спіралі лампи розжарювання від температури. Вольфрамову спіраль можна вважати сірим тілом, для якого виконується співвідношення (61.10). При високих температурах потужність, що підводиться до спіралі лампи (W=IU) майже повністю витрачається на випромінювання. Використовуючи закон Стефана-Больцмана і співвідношення (61.8), знаходимо:

(61.9)

де струм, що проходить по спіралі; напруга; площа випромінювання (поверхні спіралі); температура спіралі. Величина відповідає потужності, що випромінюється (і поглинається) в умовах теплової рівноваги з середовищем, тобто при . Таким чином, для сталої Стефана-Больцмана одержимо розрахункову формулу:

(61.12)