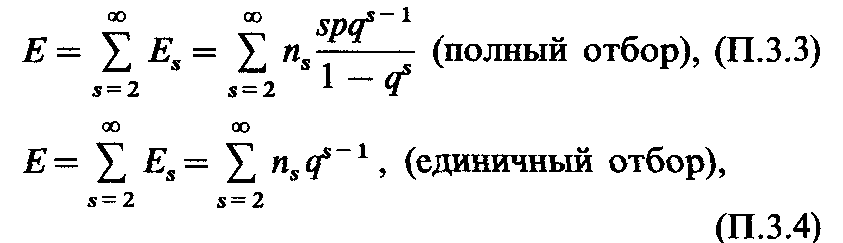- •Фогель ф., Мотульски а. Генетика человека: в 3-х т. Т. 3: Пер. С англ. – м.: Мир, 1990. – 366 с.
- •Издательство «мир»
- •7. Эволюция человека
- •7.1. Данные палеоантропологии
- •7.2. Генетические механизмы эволюция видов человека
- •7.2.1. Хромосомная эволюция и видообразование
- •10 7. Эволюция человека
- •7. Эволюция человека 13
- •7. Эволюция человека 15
- •7.2.2. Сравнение сателлитиых днк разных видов высших приматов
- •7. Эволюция человека 17
- •7.2.3 Эволюция белков [1988]
- •18 7. Эволюция человека
- •7 Эволюция человека 19
- •7. Эволюция человека 21
- •22 7. Эволюция человека
- •7. Эволюция человека 23
- •7. Эволюция человека 27
- •7.2.4. Полиморфизм длины рестрикционных фрагментов и эволюция
- •7.2.5. Поведение
- •7.2.6. Изучение ныне существующих первобытных популяций
- •7. Эволюция человека 35
- •7.3. Генетические различия между группами современных людей
- •7.3.1. Расы
- •36 7. Эволюция человека
- •7. Эволюция человека 39
- •40 7. Эволюция человека
- •42 7. Эволюция человека
- •7.3.2. Будущее рас человека: смешение рас
- •8. Генетика и поведение человека
- •8.1. Моделирование на животных
- •8. Генетика и поведение человека 49
- •8.1.1. Исследования на насекомых
- •8. Генетика и поведение человека 53
- •8.1.2. Эксперименты по генетике поведения мышей
- •8. Генетика и поведение человека 55
- •8.2. Генетика поведения человека
- •8. Генетика и поведение человека 61
- •8.2.1. Исследования с помощью классических феиомеиологических методов
- •8.2.1.1. Переоценка классических методов (см. Также гл. 3)
- •8.2.1.2. Задержка умственного развития и умственная отсталость
- •8. Генетика и поведение человека 65
- •8. Генетика и поведение человека 69
- •8.2.1.3. Интеллектуальная деятельность на нормальном и высшем уровнях
- •72 8. Генетика и поведение человека
- •74 8. Генетика и поведение человека
- •8. Генетика и поведение человека 75
- •76 8. Генетика и поведение человека
- •8. Генетика и поведение человека 77
- •78 8. Генетика и поведение человека
- •8. Генетика и поведение человека 81
- •82 8. Генетика и поведение человека
- •8.2.1.4. Специальные познавательные способности и личность
- •8. Генетика и поведение человека 83
- •8.2.1.5. «Аномальное» и социально девиантное поведение
- •90 8. Генетика и поведение человека
- •8.2.2. Хромосомные аберрации и психические расстройства
- •8. Генетика и поведение человека 91
- •8.2.2.1. Аутосомные аберрации
- •8.2.2.2. Аберрации х-хромосомы
- •5.2.2.3. Синдром χύυ
- •100 8. Генетика и поведение человека
- •8. Генетика и поведение человека 101
- •8. Генетика и поведение человека 103
- •8.2.3. Новые подходы, предложенные для исследования генетики поведения человека
- •8.2.3.1. Генетическая изменчивость, которая может влиять на поведение человека
- •8.2.3.2. Генетическая изменчивость вне мозга, влияющая на поведение человека
- •8.2.3.3. Действие гормонов
- •8.2.3.4. Физиология мозга: генетика ээг
- •8.2.3.5. Генетика алкоголизма
- •8.2.3.6. Физиология мозга: генетическая изменчивость нейромедиаторов
- •8. Генетика и поведение человека 121
- •8.2.3.7. Аффективные расстройства и шизофрения
- •8 Генетика и поведение человека 125
- •8. Генетика и поведение человека 135
- •8.2.4. Различия в iq и достижениях между этническими группами
- •136 8. Генетика и поведение человека
- •8. Генетика и поведение человека 141
- •9. Практические аспекты генетики человека и биологическое будущее человечества
- •9.1. Применения генетики человека
- •9.1.1. Генетическое консультирование [71; 90; 101; 129; 136; 149; 205; 2258; 2293; 2323а; 2351]
- •9 Практические аспекты генетики человека 143
- •9. Практические аспекты генетики человека 153
- •9.1,2. Генетический скрининг [2256; 2344; 2350]
- •9. Практические аспекты генетики человека 163
- •9.2. Манипуляции генами
- •9. Практические аспекты генетики человека 165
- •9. Практические аспекты генетики человека 169
- •9. Практические аспекты генетики человека 173
- •9.3. Биологическое будущее человечества
- •9. Практические аспекты генетики человека 175
- •9. Практические аспекты генетики человека 177
- •Приложение 1 Методы подсчета генных частот
- •182 Приложение 1
- •184 Приложение 1
- •Приложение 2 Анализ сегрегации распространенных признаков: отсутствие смещений вследствие регистрации, доминирование [876; 877]
- •Приложение 3 Формулы и таблицы для коррекции регистрационных смещений, а также для тестирования и оценки сегрегационных отношений. Другие статистические проблемы и вычислительный пример
- •192 Приложение 3
- •194 Приложение 3
- •Приложение 4 Мультифакториальное наследование и главные гены
- •204 Приложение 4
- •206 Приложение 4
- •208 Приложение 4
- •Приложение 5 Диагностика зиготности
- •Приложение 6 Вычисление коэффициента наследуемости по близнецовым данным
- •224 Приложение 6
- •Приложение 7 Метод путевых коэффициентов
- •230 Приложение 7
- •Приложение 8 Медико-генетическое консультирование: использование условных вероятностей
- •234 Приложение 8
- •236 Приложение 8
- •240 Приложение 8
- •Приложение 9 Примеры расчета сцепления
- •Литература
- •252 Литература
- •Литература к введению и главе 1
- •Литература к главе 2
- •256 Литература
- •258 Литература
- •260 Литература
- •262 Литература
- •Литература к главе 3 и к приложениям 1, 2, 3, 4, 5, 6, 7, 9
- •266 Литература
- •270 Литература
- •Литература к главе 4
- •278 Литература
- •282 Литература
- •284 Литература
- •286 Литература
- •288 Литература
- •Литература к главе 5
- •290 Литература
- •Литература к главе 6
- •300 Литература
- •302 Литература
- •304 Литература
- •Литература к главе 7
- •306 Литература
- •Литература к главе 8
- •308 Литература
- •310 Литература
- •Литература к главе 9 и приложению 8
- •Предметный указатель1)
- •324 Предметный указатель
- •344 Предметный указатель
- •356 Предметный указатель
- •364 Предметный указатель
- •Оглавление
- •7. Эволюция человека 5
- •8. Генетика и поведение человека . . 47
- •9. Практические аспекты генетики человека и биологическое будущее человечества 142
- •Электронное оглавление
- •7. Эволюция человека 5
- •8. Генетика и поведение человека 63
- •9. Практические аспекты генетики человека и биологическое будущее человечества 213
- •Назад к электронному оглавлению
192 Приложение 3
зайца из дохлой кошки. (Между прочим, один большой секрет французской кухни заключается в настойчивом требовании использовать только очень хорошие ингредиенты.)
Проблемы, связанные с тестированием статистических гипотез
Генетическая гетерогенность. Описанные выше методы дают удовлетворительные результаты, когда изучаемый признак генетически гомогенен и тип наследования простой. При этих условиях метод тестирования обнаруживает согласие между ожидаемыми и наблюдаемыми значениями и дает оценку р, близкую к ожидаемому сегрегационному отношению (25% в случае рецессивного наследования). Но даже в этом случае остается открытым вопрос о количестве вовлеченных генов с одинаковым типом наследования, т.е. вопрос о том, существует ли генетическая гетерогенность. Чтобы ответить на него, надо обследовать детей от брака двух гетерозигот. Если все их дети поражены, можно сделать вывод об участии одного и того же локуса.
При рецессивном наследовании о генетической гетерогенности можно судить, исходя из относительных частот близкородственных браков (особенно браков двоюродных братьев и сестер) среди родителей пробандов и в общей популяции (разд. 3.6.1). Это отношение возрастает с уменьшением частоты гена. Следовательно, если уровень родства намного выше, чем ожидается на основе генной частоты, вычисленной из наблюдаемой частоты признака в предположении одного рецессивного гена, то можно заключить, что существует более одного рецессивного гена. Частоты отдельных генов будут ниже, чем их суммарная частота, что и объясняет более высокий уровень родства.
Хотя теоретически такой аргумент убедителен, на практике его следует использовать очень осторожно, поскольку он предполагает случайное распределение близкородственных браков в популяции. Но семьи с рецессивными болезнями часто будут попадать в выборку из полуизолятов, в которых доля близкородственных браков
обычно выше, чем в общей популяции. Следовательно, этим аргументом можно пользоваться только вместе с другими фактами. Примесь спорадических случаев. Другая проблема возникает, когда реальное сегрегационное отношение оказывается ниже, чем ожидаемое. Здесь наиболее очевидное объяснение - примесь спорадических случаев (ненаследственных вариантов или новых доминантных мутаций). Тогда количество сибств только с одним пораженным должно быть выше его ожидаемого значения (Е), которое в соответствии с биномиальным распределением равно |
|
где ns - число сибств размера s. Это ожидаемое значение можно вычислить, если подставить вместо p оценку p, а затем сравнить его с ожидаемой частотой О, подсчитав |
|
который распределен приблизительно нормально, |
|
Пример приводится в конце данного приложения. Эта проблема не имеет практического значения в условиях полного доминирования: случай классифицируется как спорадический (ненаследственный или новая мутация), если оба родителя здоровы. Иная ситуация имеет место при неполной пенетрантности. Здесь этот метод может помочь провести различие между случаями, в которых ген присутствовал у одного из родителей, но не проявился, и реальными спорадическими случаями с генотипически нормальными родителями, т.е. новыми мутациями. Это особенно важно, когда у нас есть основания предполагать рецессивное наследование, а оценка p меньше 0,25. В такой ситуации, когда анализ показывает, что число сибств только с одним пораженным возросло, нам может понадобиться оценка истинного сегрегационного отношения. Существуют два способа получения таких оценок. Во-первых, анализ может быть ограничен сибствами по крайней мере с двумя пораженными. Во-вторых, сибствами, в которых роди- |
Приложение 3 193
Таблица П.3.2. Вычисление эффектов порядка рождения. Среднее значение (жирный шрифт) и дисперсия величины 6А в полном сибстве [698]
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
9 |
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
12 |
24 |
36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
24 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
15 |
30 |
45 |
60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
45 |
60 |
45 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
18 |
36 |
54 |
72 |
90 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
72 |
108 |
108 |
72 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
21 |
42 |
63 |
84 |
105 |
126 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
105 |
168 |
189 |
168 |
105 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
24 |
48 |
72 |
96 |
120 |
144 |
168 |
|
|
|
|
|
|
|
|
|
|
|
|
|
144 |
240 |
288 |
288 |
240 |
144 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
27 |
54 |
81 |
108 |
135 |
162 |
189 |
216 |
|
|
|
|
|
|
|
|
|
|
|
|
189 |
324 |
405 |
432 |
405 |
324 |
189 |
0 |
|
|
|
|
|
|
|
|
|
|
|
9 |
30 |
60 |
90 |
120 |
150 |
180 |
210 |
240 |
270 |
_ |
|
_ |
_ |
_ |
_ |
_ |
_ |
_ |
_ |
|
240 |
420 |
540 |
600 |
600 |
540 |
420 |
240 |
0 |
|
|
|
|
|
|
|
|
|
|
10 |
33 |
66 |
99 |
132 |
165 |
198 |
231 |
264 |
297 |
330 |
_ |
— |
_ |
_ |
_ |
_ |
_ |
— |
_ |
|
297 |
528 |
693 |
792 |
825 |
792 |
693 |
528 |
297 |
0 |
|
|
|
|
|
|
|
|
|
11 |
36 |
72 |
108 |
144 |
180 |
216 |
252 |
288 |
324 |
360 |
396 |
_ |
_ |
_ |
_ |
_ |
_ |
— |
_ |
|
360 |
648 |
864 |
1008 |
1080 |
1080 |
1008 |
864 |
648 |
360 |
0 |
|
|
|
|
|
|
|
|
12 |
39 |
78 |
117 |
156 |
195 |
234 |
273 |
312 |
351 |
390 |
429 |
468 |
_ |
_ |
_ |
_ |
_ |
_ |
_ |
|
429 |
780 |
1053 |
1248 |
1365 |
1404 |
1365 |
1248 |
1053 |
780 |
429 |
0 |
|
|
|
|
|
|
|
13 |
42 |
84 |
126 |
168 |
210 |
252 |
294 |
336 |
378 |
420 |
462 |
504 |
546 |
_ |
_ |
_ |
_ |
_ |
_ |
|
504 |
924 |
1260 |
1512 |
1680 |
1764 |
1764 |
1680 |
1512 |
1260 |
924 |
504 |
0 |
|
|
|
|
|
|
14 |
45 |
90 |
135 |
180 |
225 |
270 |
315 |
360 |
405 |
450 |
495 |
540 |
585 |
630 |
_ |
_ |
_ |
_ |
_ |
|
585 |
1080 |
1485 |
1800 |
2025 |
2160 |
2205 |
2160 |
2025 |
1800 |
1485 |
1080 |
585 |
0 |
|
|
|
|
|
15 |
48 |
96 |
144 |
192 |
240 |
288 |
336 |
384 |
432 |
480 |
528 |
576 |
624 |
672 |
720 |
_ |
_ |
_ |
_ |
|
672 |
1248 |
1728 |
2112 |
2400 |
2592 |
2688 |
2688 |
2592 |
2400 |
2112 |
1728 |
1248 |
672 |
0 |
|
|
|
|
16 |
51 |
102 |
153 |
204 |
255 |
306 |
357 |
408 |
459 |
510 |
561 |
612 |
663 |
714 |
765 |
816 |
— |
_ |
_ |
|
765 |
1428 |
1989 |
2448 |
2805 |
3060 |
3213 |
3264 |
3213 |
3060 |
2805 |
2448 |
1989 |
1428 |
765 |
0 |
|
|
|
17 |
54 |
108 |
162 |
216 |
270 |
324 |
378 |
432 |
486 |
540 |
594 |
648 |
702 |
756 |
810 |
864 |
918 |
_ |
_ |
|
864 |
1620 |
2268 |
2808 |
3240 |
3564 |
3780 |
3888 |
3888 |
3780 |
3564 |
3240 |
2808 |
2268 |
1620 |
864 |
0 |
|
|
18 |
57 |
114 |
171 |
228 |
285 |
342 |
399 |
456 |
513 |
570 |
627 |
684 |
741 |
798 |
855 |
912 |
969 |
1026 |
_ |
|
969 |
1824 |
2565 |
3192 |
3705 |
4104 |
4389 |
4560 |
4617 |
4560 |
4389 |
4104 |
3705 |
3192 |
2565 |
1824 |
969 |
0 |
|
19 |
60 |
120 |
180 |
240 |
300 |
360 |
420 |
480 |
540 |
600 |
660 |
720 |
780 |
840 |
900 |
960 |
1020 |
1080 |
1140 |
|
1080 |
2040 |
2880 |
3600 |
4200 |
4680 |
5040 |
5280 |
5400 |
5400 |
5280 |
5040 |
4680 |
4200 |
3600 |
2880 |
2040 |
1080 |
0 |
20 |
63 |
126 |
189 |
252 |
315 |
378 |
441 |
504 |
567 |
630 |
693 |
756 |
819 |
882 |
945 |
1008 |
1071 |
1134 |
1197 |
|
1197 |
2268 |
3213 |
4032 |
4725 |
5292 |
5733 |
6048 |
6237 |
6300 |
6237 |
6048 |
5733 |
5292 |
4725 |
4032 |
3213 |
2268 |
1197 |