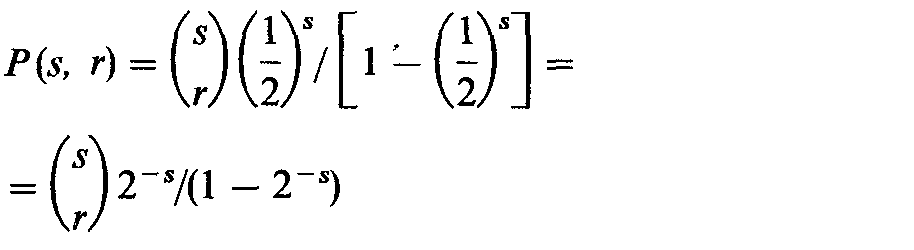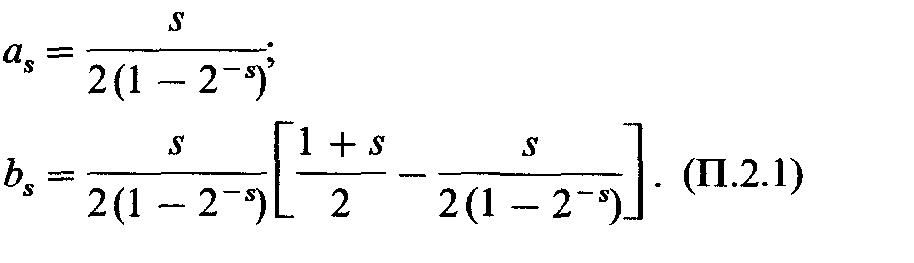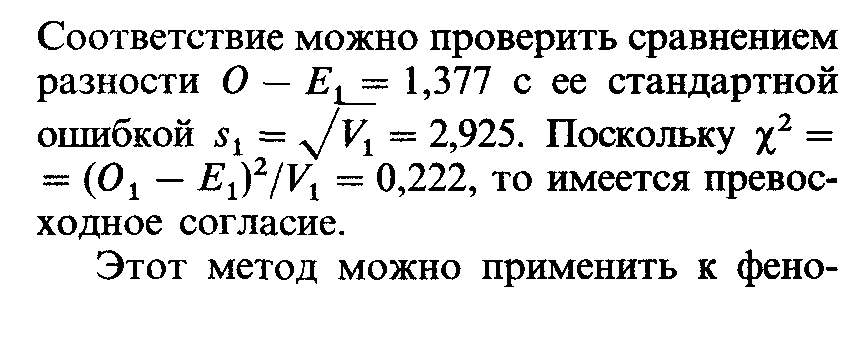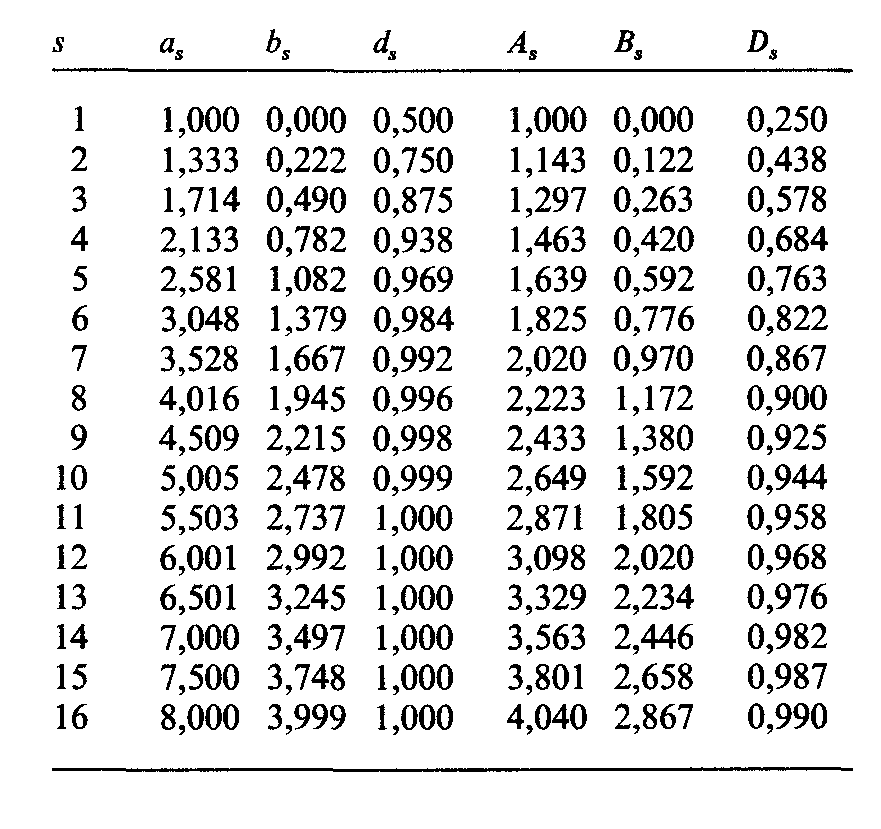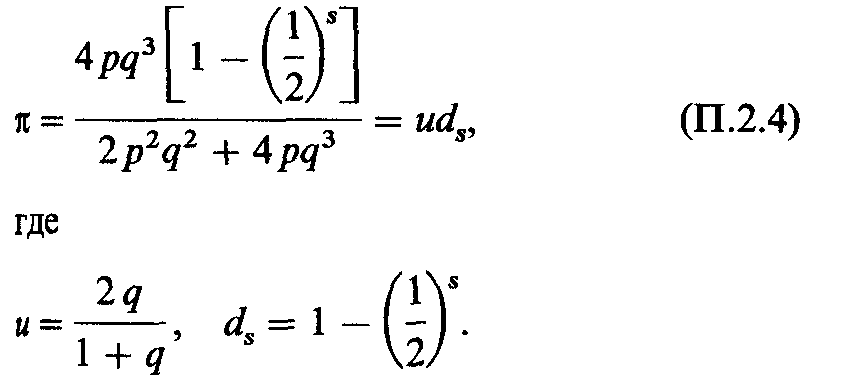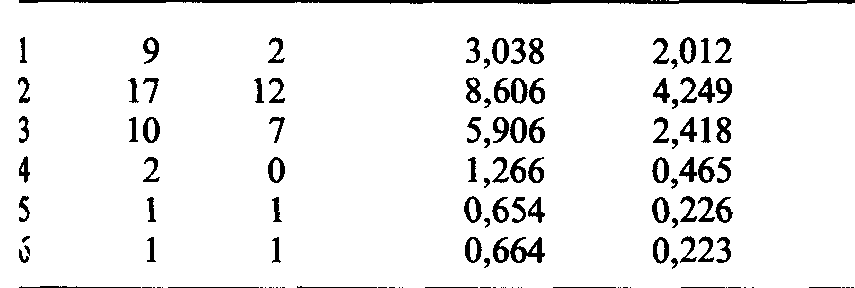- •Фогель ф., Мотульски а. Генетика человека: в 3-х т. Т. 3: Пер. С англ. – м.: Мир, 1990. – 366 с.
- •Издательство «мир»
- •7. Эволюция человека
- •7.1. Данные палеоантропологии
- •7.2. Генетические механизмы эволюция видов человека
- •7.2.1. Хромосомная эволюция и видообразование
- •10 7. Эволюция человека
- •7. Эволюция человека 13
- •7. Эволюция человека 15
- •7.2.2. Сравнение сателлитиых днк разных видов высших приматов
- •7. Эволюция человека 17
- •7.2.3 Эволюция белков [1988]
- •18 7. Эволюция человека
- •7 Эволюция человека 19
- •7. Эволюция человека 21
- •22 7. Эволюция человека
- •7. Эволюция человека 23
- •7. Эволюция человека 27
- •7.2.4. Полиморфизм длины рестрикционных фрагментов и эволюция
- •7.2.5. Поведение
- •7.2.6. Изучение ныне существующих первобытных популяций
- •7. Эволюция человека 35
- •7.3. Генетические различия между группами современных людей
- •7.3.1. Расы
- •36 7. Эволюция человека
- •7. Эволюция человека 39
- •40 7. Эволюция человека
- •42 7. Эволюция человека
- •7.3.2. Будущее рас человека: смешение рас
- •8. Генетика и поведение человека
- •8.1. Моделирование на животных
- •8. Генетика и поведение человека 49
- •8.1.1. Исследования на насекомых
- •8. Генетика и поведение человека 53
- •8.1.2. Эксперименты по генетике поведения мышей
- •8. Генетика и поведение человека 55
- •8.2. Генетика поведения человека
- •8. Генетика и поведение человека 61
- •8.2.1. Исследования с помощью классических феиомеиологических методов
- •8.2.1.1. Переоценка классических методов (см. Также гл. 3)
- •8.2.1.2. Задержка умственного развития и умственная отсталость
- •8. Генетика и поведение человека 65
- •8. Генетика и поведение человека 69
- •8.2.1.3. Интеллектуальная деятельность на нормальном и высшем уровнях
- •72 8. Генетика и поведение человека
- •74 8. Генетика и поведение человека
- •8. Генетика и поведение человека 75
- •76 8. Генетика и поведение человека
- •8. Генетика и поведение человека 77
- •78 8. Генетика и поведение человека
- •8. Генетика и поведение человека 81
- •82 8. Генетика и поведение человека
- •8.2.1.4. Специальные познавательные способности и личность
- •8. Генетика и поведение человека 83
- •8.2.1.5. «Аномальное» и социально девиантное поведение
- •90 8. Генетика и поведение человека
- •8.2.2. Хромосомные аберрации и психические расстройства
- •8. Генетика и поведение человека 91
- •8.2.2.1. Аутосомные аберрации
- •8.2.2.2. Аберрации х-хромосомы
- •5.2.2.3. Синдром χύυ
- •100 8. Генетика и поведение человека
- •8. Генетика и поведение человека 101
- •8. Генетика и поведение человека 103
- •8.2.3. Новые подходы, предложенные для исследования генетики поведения человека
- •8.2.3.1. Генетическая изменчивость, которая может влиять на поведение человека
- •8.2.3.2. Генетическая изменчивость вне мозга, влияющая на поведение человека
- •8.2.3.3. Действие гормонов
- •8.2.3.4. Физиология мозга: генетика ээг
- •8.2.3.5. Генетика алкоголизма
- •8.2.3.6. Физиология мозга: генетическая изменчивость нейромедиаторов
- •8. Генетика и поведение человека 121
- •8.2.3.7. Аффективные расстройства и шизофрения
- •8 Генетика и поведение человека 125
- •8. Генетика и поведение человека 135
- •8.2.4. Различия в iq и достижениях между этническими группами
- •136 8. Генетика и поведение человека
- •8. Генетика и поведение человека 141
- •9. Практические аспекты генетики человека и биологическое будущее человечества
- •9.1. Применения генетики человека
- •9.1.1. Генетическое консультирование [71; 90; 101; 129; 136; 149; 205; 2258; 2293; 2323а; 2351]
- •9 Практические аспекты генетики человека 143
- •9. Практические аспекты генетики человека 153
- •9.1,2. Генетический скрининг [2256; 2344; 2350]
- •9. Практические аспекты генетики человека 163
- •9.2. Манипуляции генами
- •9. Практические аспекты генетики человека 165
- •9. Практические аспекты генетики человека 169
- •9. Практические аспекты генетики человека 173
- •9.3. Биологическое будущее человечества
- •9. Практические аспекты генетики человека 175
- •9. Практические аспекты генетики человека 177
- •Приложение 1 Методы подсчета генных частот
- •182 Приложение 1
- •184 Приложение 1
- •Приложение 2 Анализ сегрегации распространенных признаков: отсутствие смещений вследствие регистрации, доминирование [876; 877]
- •Приложение 3 Формулы и таблицы для коррекции регистрационных смещений, а также для тестирования и оценки сегрегационных отношений. Другие статистические проблемы и вычислительный пример
- •192 Приложение 3
- •194 Приложение 3
- •Приложение 4 Мультифакториальное наследование и главные гены
- •204 Приложение 4
- •206 Приложение 4
- •208 Приложение 4
- •Приложение 5 Диагностика зиготности
- •Приложение 6 Вычисление коэффициента наследуемости по близнецовым данным
- •224 Приложение 6
- •Приложение 7 Метод путевых коэффициентов
- •230 Приложение 7
- •Приложение 8 Медико-генетическое консультирование: использование условных вероятностей
- •234 Приложение 8
- •236 Приложение 8
- •240 Приложение 8
- •Приложение 9 Примеры расчета сцепления
- •Литература
- •252 Литература
- •Литература к введению и главе 1
- •Литература к главе 2
- •256 Литература
- •258 Литература
- •260 Литература
- •262 Литература
- •Литература к главе 3 и к приложениям 1, 2, 3, 4, 5, 6, 7, 9
- •266 Литература
- •270 Литература
- •Литература к главе 4
- •278 Литература
- •282 Литература
- •284 Литература
- •286 Литература
- •288 Литература
- •Литература к главе 5
- •290 Литература
- •Литература к главе 6
- •300 Литература
- •302 Литература
- •304 Литература
- •Литература к главе 7
- •306 Литература
- •Литература к главе 8
- •308 Литература
- •310 Литература
- •Литература к главе 9 и приложению 8
- •Предметный указатель1)
- •324 Предметный указатель
- •344 Предметный указатель
- •356 Предметный указатель
- •364 Предметный указатель
- •Оглавление
- •7. Эволюция человека 5
- •8. Генетика и поведение человека . . 47
- •9. Практические аспекты генетики человека и биологическое будущее человечества 142
- •Электронное оглавление
- •7. Эволюция человека 5
- •8. Генетика и поведение человека 63
- •9. Практические аспекты генетики человека и биологическое будущее человечества 213
- •Назад к электронному оглавлению
184 Приложение 1
методом Бернштейна это дает следующие результаты (подробнее в разд. 3.2.2):
p = 0,287685 + 0,002411, q = 0,106555 ±0,001545, r = 0,605760 ±0,002601.
Было показано, что метод максимального правдоподобия приводит к точно таким же результатам [711]. Дисперсии по методу максимального правдоподобия получились следующими:
Vp = 0,000005811, Vq = 0,000002386, Vr = 0,000006763.
Для получения стандартных отклонений нужно извлечь квадратные корни из этих дисперсий.
Точно так же, как было показано для групп крови MN, по частоте аллелей А, В и О можно вычислить ожидаемые генотипические частоты и сравнить их с наблюдаемыми частотами по критерию хи-квадрат.
Еще более сложные проблемы возникают при анализе групп крови Rh и вообще при анализе всех систем, в которых вместе
наследуется много разных комбинаций антигенов. Для этих случаев опубликованы или упомянуты в публикациях компьютерные программы. Для системы Rh можно воспользоваться публикациями [585; 586]. Рядом авторов предложены правила вычисления частот аллелей и гаплотипов для системы HLA [554; 738; 779; 805; 962]. Находит свое применение также система ALLTYPE [789].
Однако неадекватность составления выборки не компенсируется обработкой на компьютере. Все упомянутые до сих пор методы основаны на предположении, что выбор индивидов проводился независимо, т .е. выбор какого-либо одного индивида не увеличивает и не уменьшает шанс быть выбранным для любого другого индивида в популяции. Это правило нарушается, например, при сборе данных о родственниках. Однако нельзя сказать, что выборки, содержащие родственников, всегда бесполезны для вычисления генных частот. Но включение родственников в выборку должно быть обязательно отмечено вместе со степенью их родства, и для анализа должны использоваться специальные статистические методы [211].
Приложение 2 Анализ сегрегации распространенных признаков: отсутствие смещений вследствие регистрации, доминирование [876; 877]
Если тип наследования кодоминантный, так что каждый генотип соответствует своему, отличному от других фенотипу, и если анализируемые семьи выбирались из популяции независимо от генотипов их членов, то анализ сегрегационных отношений проводится непосредственно. В этом случае число. индивидов в каждом генотипическом классе следует сравнивать с числом, ожидаемым из распределения на основе менделевского закона, с помощью критерия хи-квадрат, как показано в разд. 3.3.3 и табл. 3.7. |
При доминировании сегрегационный анализ сложнее, чем при кодоминантном наследовании. В фенотипическом браке |
|
АА x Аа и Аа x Аа. Оригинальный метод сегрегационного анализа был разработан Смитом [876]. |
Тип брака А x а. В этой группе представлены два генотипических брака АА x аа и Аа x аа. Первый дает только детей с генотипом Аа и с фенотипом А, а второй - детей Аа и аа в соотношении 1:1. Для иллюстрации используются данные по группам крови (табл. П.2.1, П.2.2). Ниже приводятся численности семей по крайней мере с одним рецессивным ребенком (аналог регистрации семей по «пораженным» потомкам) |
|
Ожидается, что в этих семьях число детей с рецессивным фенотипом подчиняется «усеченному биномиальному распределению» Например, ожидаемое соотношение двухдетных семей с 0, 1 или 2 рецессивными |
детьми должно быть равным 1:2:1. Однако класс с нулем рецессивов отсутствует в силу способа регистрации. Следовательно, с вероятностью 2/3 двухдетная семья будет иметь одного рецессивного потомка и с вероятностью 1/3 - двух. Ожидаемое число рецессивных детей в двухдетных семьях равно |
|
а дисперсия |
|
В принципе те же рассуждения можно использовать для семей с 3, 4 и большим числом детей и вычислить а3, a4 ··· и b3, b4... . В общем случае вероятность того, что семья из s детей по крайней мере с одним рецессивным ребенком имеет точно r рецессивных детей, равна |
|
(ср. с биномиальным распределением, разд. 3.3.2). Отсюда вытекает, что |
|
Ожидаемое общее число детей с рецессивным фенотипом в выборке составит |
|
(используя данные Смита, приведенные здесь в табл. П.2.3). Дисперсию этой величины можно вычислить из аналогичной |
186 Приложение 2
Таблица
П.2.1. Фенотипический брак |
|
линейной комбинации значений b v1 = 8,555. Общий вид формул следующий: |
|
Наблюдаемое число рецессивов (из табл. П.2.1) равно |
O1 = 11 χ 1 + 10 χ 2 + 2 χ 3 = 37. |
|
Таблица П. 2.2.
Фенотипический брак |
|
типическому браку А х А (табл. П.2.2) с той лишь разницей, что в браке Аа х Аа дети с фенотипами А и а ожидаются в соотношении 3:1. Ожидаемые средние значения As и дисперсии Bs можно взять из табл. П.2.3. В 10 семьях по крайней мере с одним ребенком наблюдались 11 таких детей. Сравнивая эту величину с ожидаемым средним значением Е2 = 12,3 и дисперсией V2 = 2,069, получаем |
|
Снова наблюдаемые значения превосходно соответствуют ожидаемым. |
До сих пор мы не использовали генные частоты. Наблюдаемые численности семей по крайней мере с одним рецессивным ребенком нужно сравнить с ожидаемыми численностями таких семей, рассчитанными из общего количества семей в выборке. Для этого необходимы надежные оценки генных частот. Их можно получить, имея большую выборку случайных индивидов из популяции. Фенотипический брак Axa, например, может включать два генотипических АА х аа и Аа х аа. Их ожидаемая частота |
Таблица П.2.3. Ожидаемые средние значения аs, дисперсии bs и величины ds для фенотипического брака A x a. Ожидаемые средние значения As, дисперсии Bs и величины Ds для фенотипического брака А х А [876] |
|
Приложение 2 187
2 x ρ2 x q2 + 2 x 2pq x q2 = 2p2q2 + 4pq3. В то же время это значение является вероятностью того, что случайно выбранный брак будет иметь фенотип А х а. На самом деле семья может иметь рецессивного ребенка, только если генотипический брак будет Аа х аа. Даже в этом случае вероятность иметь по крайней мере одного рецессивного ребенка среди s детей равна 1 - (l/2)s, т. к. с вероятностью (1/2)S будут появляться только доминантные дети. |
По этой причине вероятность π того, что семья типа Аха с s детьми будет иметь по крайней мере одного рецессивного ребенка, составит |
|
Значения ds приведены в табл. П.2.3, и когда известны генные частоты, то легко вычислить uds. Если имеется ns семей размера s (s = l, 2, ...), то ожидаемые среднее значение и дисперсия числа семей по крайней мере с одним рецессивным ребенком составят |
|
Таблица П.2.4. Ожидаемые и наблюдаемые частоты семей с рецессивными детьми, фенотипический брак А х à |
|
|
|
Таблица П.2.5. Ожидаемые и наблюдаемые частоты семей с рецессивными детьми, фенотипический брак ÄxÄ |
|
Например, генная частота q рецессивного аллеля ρ в системе Ρ равна 0,51. Следовательно, и = 0,675. Дальнейшие вычисления приведены в табл. П.2.4. |
В принципе те же расчеты можно выполнить для А х А семей с u2 и Ds = 1 — — (3/4)s вместо u и d соответственно; значения Ds приведены в табл. П.2.5. |
Все сравнения собраны вместе в табл. П.2.6, где приведена также сумма всех сравнений. В первых двух строках таблицы представлены значения критерия хи-квадрат для сравнения с ожидаемыми сегрегационными отношениями, а в следующих двух - наблюдаемые частоты разных типов брака сравниваются с ожидаемыми на основе закона Харди-Вайнберга, при этом используются генные частоты. Такое четкое разделение делает метод более понятным. |
Таблица П.2.6. 2-сравнения |
|
|
|