Определение кратчайших расстояний с использованием метода потенциалов

Задана транспортная сеть (рисунок 2.1). Пункты транспортной сети представляют собой вершины, обозначенные буквами от 1 до 10. Заданы расстояния между пунктами, т. е. определены звенья сети и их длина.

Задача решается следующим образом.

Шаг I. Вершина, от которой требуется определить кратчайшие расстояния, называется начальной. Начальной вершине присваивается нулевой потенциал Ui = 0.

Шаг II. Просматриваются все звенья, начальные вершины i которых имеют потенциалы Ui, а конечные j – не имеют. Определяется значение потенциалов конечных вершин Uj по следующей формуле:

Uj = Ui + Cij

где Cij — длина звена (i – j), т. е. расстояние между вершинами i и j.

Из всех полученных потенциалов выбирается наименьший (поскольку определяются кратчайшие расстояния), и его значение присваивается соответствующей конечной вершине. Звено (i – j) отмечается стрелкой.

Шаг II повторяется до тех пор, пока всем вершинам данной сети не будут присвоены потенциалы.

Величина потенциалов у соответствующих вершин показывает кратчайшее расстояние от выбранного начального пункта до данного пункта. Звенья со стрелками образуют кратчайший маршрут движения от начального пункта ко всем остальным.

Принимая за начало сети последовательно каждый ее пункт (вершину) и выполняя расчеты по описанному методу, можно получить таблицу кратчайших расстояний между всеми пунктами сети.

Этап 1: примем нулевой потенциал в вершине 1.

Рисунок 2.2. Кратчайшие расстояния из вершины 1 относительно других вершин.

Расчеты:

Этап 2: примем нулевой потенциал в вершине 2.

Рисунок 2.3. Кратчайшие расстояния из вершины 2 относительно других вершин.

Расчеты:

U₉=U₈+C_8-9=18+6 = 24

Этап 3: примем нулевой потенциал в вершине 3.

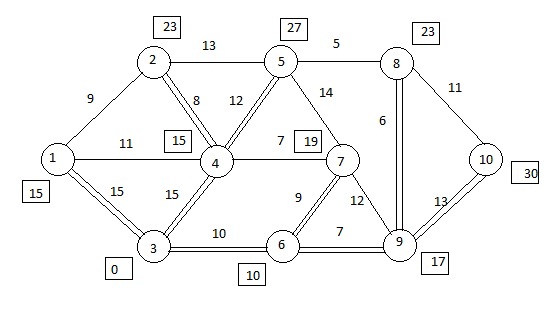
Рисунок 2.4. Кратчайшие расстояния из вершины 3 относительно других вершин.

Расчеты:

Этап 4: примем нулевой потенциал в вершине 4.

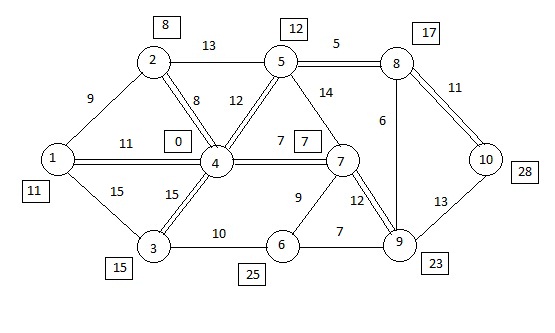
Рисунок 2.5. Кратчайшие расстояния из вершины 4 относительно других вершин.

Расчеты:

Этап 5: примем нулевой потенциал в вершине 5.

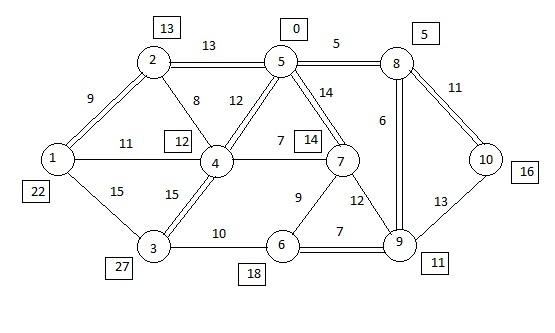
Рисунок 2.6. Кратчайшие расстояния из вершины 5 относительно других вершин.

Расчеты:

Этап 6: примем нулевой потенциал в вершине 6.

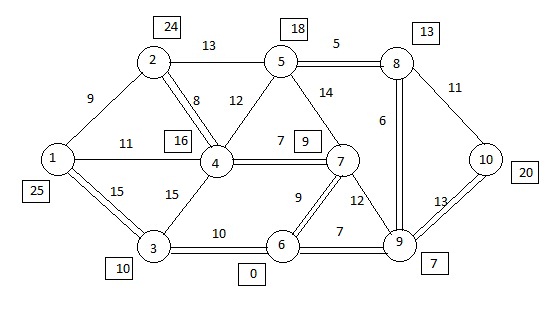
Рисунок 2.7. Кратчайшие расстояния из вершины 6 относительно других вершин.

Расчеты:

U₅ =U₈ + C_5-8 = 13 + 5 = 18

Этап 7: примем нулевой потенциал в вершине 7.

Рисунок 2.8. Кратчайшие расстояния из вершины 7 относительно других вершин.

Расчеты:

Этап 8: примем нулевой потенциал в вершине 8.

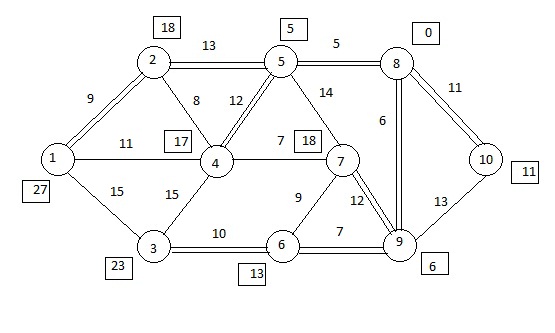
Рисунок 2.9. Кратчайшие расстояния из вершины 8 относительно других вершин.

Расчеты:

Этап 9: примем нулевой потенциал в вершине 9.

Рисунок 2.10. Кратчайшие расстояния из вершины 9 относительно других вершин.

Расчеты:

Этап 10 можно не рассчитывать, так как маршрут 1-10=10-1; 2-10=10-2; 3-10=10-3; 4-10=10-4; 5-10=10-5; 6-10=10-6; 7-10=10-7; 8-10=10-8; 9-10=10-9.

На основании проведенных расчетов может быть составлена таблица кратчайших расстояний между пунктами транспортной сети (таблица 2.1).

Рассмотренный метод весьма прост и используется для составления таблиц кратчайших расстояний между пунктами сети вручную.

Так как расстояние между одноименными пунктами равно нулю то в таблице 2.1 расстояния между этими пунктами не проставлены.

Таблица 2.1

Кратчайшие расстояния между пунктами транспортной сети

Пункты	1	2	3	4	5	6	7	8	9	10
1		9	15	11	22	25	18	27	30	38
2	9		23	8	13	24	15	18	24	29
3	15	23		15	27	10	19	23	17	30
4	11	8	15		12	-	7	17	23	28
5	22	13	27	12		18	14	5	11	16
6	25	24	10	- *	18		9	13	7	20
7	18	15	19	7	14	9		-	12	25
8	27	18	23	17	5	13	-		6	11
9	30	24	17	23	11	7	12	6		13
10	38	29	30	28	16	20	25	11	13

*4-6 и 7-8 считаются закрытыми для движения грузового автотранспорта