1.3.2. Уравнение состояния термодинамической системы

Все термодинамические параметры гомогенной сисемы (однородной – с одинаковыми физическими свойствами), находящейся в равновесном состоянии, имеют определенную функциональную связь. При отсутствии действия внешних полей термодинамически равновесное состояние любого однородного реального тела определяется всего лишь двумя независимыми параметрами. Для неоднородных систем могут два параметра взаимно определять друг друга (например, давление и температура влажного насыщенного пара), в этом случае необходим третий параметр.

В качестве независимых параметров могут быть выбраны: давление и температура, давление и удельный объём или любая пара независимых свойств (температура и энтропия, давление и энтальпия и т.п.).

При заданных значениях двух параметров термодинмически равновесной системы можно определить любые другие ее параметры. Связь между параметрами такой системы описывается уравнениями состояния. Например, связь между параметрами p, v, T может быть выражена термическими уравнениями состояния системы:

- в неявной форме f(p,v,T) = 0 , (1.12)

- в явной форме p = F(v,T); v = f(p,T); T = j(p,v). (1.13)

В системе координат P,v,T эти уравнения описывают поверхность, называемую термодинамической (рис. 1.8).

В ид функциональной зависимости между параметрами различен для различных веществ и может быть получен либо из опыта, либо на базе микрофизических теорий. Методами самой термодинамики эта связь определена быть не может.

1.3.3. Термические коэффициенты

Взаимосвязь свойств однородного вещества в равновесном состоянии может также характеризоваться термическими коэффициентами. Эти коэффициенты могут быть определены опытным путем, они имеют определенный физический смысл.

Взаимосвязь термических коэффициентов можно получить, используя уравнение состояния вещества в явном виде Р=F(v,T), представив его как полный дифференциал

; (1.14)

приняв Р = const, получим

,

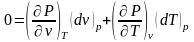преобразовав это выражение, получим соотношение вида

. (1.15)

В выражении (1.15) отношение (dv/dP)_T характеризует интенсивность изменения объема в зависимости от изменения давления при постоянной температуре. Отношение этой величины к удельному объему v_o, взятому при фиксированном состоянии (например, при нормальных условиях) с обратным знаком, называется коэффициентом изотермической сжимаемости и обозначается как m:

. (1.16)

Отношение (dv/dТ)_Р характеризует интенсивность изменения объема в зависимости от изменения температуры при постоянном давлении. Разделив его на v_о, получим коэффициент изобарного расширения, обозначающийся как a:

. (1.17)

Отношение (dР/dТ)_v характеризует изменение давления в зависимости от изменения температуры при постоянном объеме. Разделив его на Р_о, получим коэффициент упругости, обозначающийся как b:

. (1.18)

Выразив значения частных производных в выражении (1.15) через термические коэффициенты (dv/dP)_T=-mv_o , (dv/dТ)_P=av_o , (dР/dТ)_v=bP_o и подставив их в (1.15), получим уравнение взаимосвязи термических коэффициентов:

. (1.19)

Выражение (1.19), как и уравнение состояния, описывает свойства вещества. Кроме этого, выражение (1.19) необходимо для расчета коэффициента b твердых и жидких тел, поскольку эти тела невозможно нагреть без изменения их объема, т.е. b для них опытным путем определить невозможно.