4.4. Установление показателя политропы по опытным данным

Все, что было изложено ранее относительно политропных процессов, применимо к идеальным газам с постоянной изохорной теплоемкостью – с_v. Для реальных газов изохорная теплоемкость величина переменная, следовательно, политропному процессу реального газа, отвечающему соотношению du/q==const, будет соответствовать переменная теплоемкость с=сv/. Переменная величина теплоемкости политропного процесса реального газа приводит к сложным зависимостям между термическими и энергетическими параметрами газа в таких процессах. Однако с достаточной для технических расчетов степенью точности для реальных газов можно использовать большинство полученных ранее формул для политропного процесса идеального газа [8], понимая при этом под политропным процессом реального газа процесс, удовлетворяющий уравнению

Pvⁿ=const.

Величина показателя политропы n считается постоянной. Для уменьшения погрешности расчетов изохорную теплоемкость с_v берут как среднюю c_vm в интервале температур рассматриваемого процесса. Используя среднюю изохорную теплоемкость реального газа, можно приближенно рассчитать показатель политропы n. По заданной величине  определяют среднее значение теплоемкости политропного процесса на данном интервале температур как с_m=с_vm/, и по этой теплоемкости рассчитывается показатель политропы:

, (a)

где с_рm=c_vm+R.

При экспериментальном исследовании процессов изменения состояния газов получают опытные данные серии мгновенных значений термических параметров в виде графического или цифрового материала. Для проведения термодинамического анализа таких процессов необходимо установить, являются ли они политропными. В случае, если процесс соответствует политропному процессу, необходимо определить показатель политропы n. Если весь процесс не может рассматриваться как политропный, то он может быть разделен на участки, которые с достаточной степенью точности могут рассматриваться как политропные, и для каждого из этих участков определяется свое среднее значение показателя политропы n.

Рассмотрим некоторые из методов обработки и анализа опытных данных закономерных газовых процессов.

Оценить, относится газовый процесс к политропному или нет, наиболее просто, изобразив его в логарифмических координатах LnP–Lnv. Прологарифмировав уравнение политропы Pvⁿ=const, получим уравнение

LnP + nLnv = A. (б)

В логарифмической системе координат LnP–Lnv это уравнение прямой линии. Следовательно, нанеся опытные точки процесса в данной системе координат, можно сделать вывод, относится ли данный процесс к политропному. Если все опытные точки ложатся на одну прямую (рис.4.9), то процесс подчиняется уравнению политропы Pvⁿ=const. Если точки не ложатся на одну прямую, то это не политропный процесс. Однако в этом случае может быть проведена аппроксимация опытных точек с заменой действительного процесса политропным. Оценить пригодность такой политропы для расчетов процесса с заданной степенью точности можно по отклонению опытных точек от политропы.

Д ля политропного процесса, изображенного в виде прямой в системе координат LnP–Lnv, показатель политропы легко определяется из уравнения (б) в виде углового коэффициента, который можно выразить через отношение отезков (см. рис.4.9):

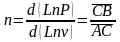. (в)

На рис.4.10 изображены политропные процессы в логарифмической системе координат с различными показателями политропы: n=0 – изобара, n=1 – изотерма, n=к – адиабата, n= – изохора.

Определить показатель политропы можно и по параметрам двух точек процесса. В случае если процесс соответствует политропе, для двух его точек можно записать равенство

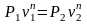или .

Прологарифмировав полученное равенство, получим расчетное выражение для показателя политропы:

,  . (г)