
- •Введение техническая термодинамика как теоретическая основа теплоэнергетики
- •1. Общие определения и понятия
- •1.1. Термодинамическая система
- •1.2. Термодинамические параметры состояния
- •Основные термические параметры состояния
- •Удельный объем
- •Давление
- •Соотношения единиц измерения давления
- •Температура
- •1.3.2. Уравнение состояния термодинамической системы
- •1.3.3. Термические коэффициенты
- •1.3.4. Термодинамический процесс
- •2. Первый закон термодинамики для закрытой системы
- •2.1. Работа изменения объема
- •2.2. Теплота, теплоемкость, энтропия
- •2.3. Внутренняя энергия
- •2.4. Первый закон термодинамики для закрытой системы
- •2.4.1. Аналитические выражения первого закона термодинамики.
- •2.4.2. Энтальпия
- •3. Газы и газовые смеси
- •3.1. Законы идеальных газов
- •3.1.1. Внутренняя энергия идеального газа
- •3.1.2. Теплоемкости газов
- •Удельные теплоемкости
- •Теплоемкости процессов
- •Теплоемкости идеальных газов
- •Теплоемкость реальных газов
- •Отношение изобарной и изохорной теплоемкостей
- •3.1.3. Энтальпия идеальных газов
- •3.1.4. Энтропия идеальных газов
- •3.2. Газовые смеси
- •Основные характеристики смеси газов
- •Теплоемкости газовых смесей
- •4. Газовые процессы
- •4.1. Политропные процессы
- •4.2. Частные случаи политропных процессов
- •Уравнения процессов, расчетные выражения их теплоты, работы, изменения внутренней энерги, энтальпии и энтропи
- •4.3. Изображение политропных процессов в р,V и t,s- диаграммах Политропа в р,V- диаграмме
- •Политропа в t,s- диаграмме
- •4.4. Установление показателя политропы по опытным данным
- •4.5. Качественный и количественный анализ политропных процессов в р,V- и t,s- диаграммах
- •4.6. Определение термодинамических свойств идеальных газов с учетом влияния температуры на их изобарную и изохорную теплоемкости
- •Определение энергетических параметров идеальных газов с учетом влияния температуры на cp и cv
Основные характеристики смеси газов
Для того чтобы воспользоваться уравнением Менделеева-Клапейрона для смеси газов
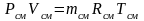 ,
,
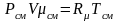 ,
,
 ,
,
необходимо знать газовую постоянную Rсм и молярную массу (условную) смеси µсм. Для смеси, как для любого идеального газа, эти две величины связаны соотношением Rсм=8314/µсм (Дж/(кг·К)). Чтобы рассчитать эти величины, необходимо знать состав смеси газов, т.е. какие газы и в какой пропорции входят в смесь.
Состав смеси может быть задан массовыми, объемными или мольными долями.
Массовой долей gi данного газа называется отношение его массы к массе всей смеси:
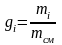 ,
(3.67)
,
(3.67)
где mi – масса отдельного газа, входящего в смесь;
mсм – общая масса смеси.
Очевидно, что сумма массовых долей всех газов смеси равна единице:
 .
(3.68)
.
(3.68)
Объeмной долей ri данного газа называется отношение объема, который занимал бы данный газ при температуре и давлении смеси, к общему объему смеси:
 ,
(3.69)
,
(3.69)
где Vi – объем данного газа при Тсм и Рсм, м3.
Объем Vi называют парциальным объемом, это искусственно введенная величина, поскольку каждый газ, входящий в смесь, занимает весь объем смеси. Парциальный объем можно рассчитать по уравнению Менделеева – Клапейрона:
 .
(3.70)
.
(3.70)
Записав уравнение Менделеева – Клапейрона через парциальное давление и через парциальный объем,
,
 ,
,
можно получить еще одно расчетное выражение для объемной доли, поделив правые и левые части этих уравнений одно на другое:
 .
(3.71)
.
(3.71)
Поскольку сумма парциальных давлений равна давлению смеси, то сумма объемных долей всех газов смеси равна единице, а сумма парциальных объемов равна полному объему всей смеси газов:
 ,
(3.72)
,
(3.72)
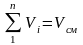 .
(3.73)
.
(3.73)
Для смеси газов используется понятие мольных долей. Мольной долей называется отношение количества молей данного газа Мi к общему количеству молей всех газов смеси Мсм.
Количество молей определяется делением массы газа на его молярную массу:
 .
(3.74)
.
(3.74)
Воспользовавшись уравнением Менделеева – Клапейрона для парциального и полного объемов смеси газов и введя в него количество молей
 ,
,
 ,
,
получим еще одно расчетное выражение для мольной доли:
 .
(3.75)
.
(3.75)
Равенство объемных и мольных долей для смеси газов можно получить и из закона Авогадро, в соответствии с которым объемы молей всех идеальных газов при одинаковых параметрах одинаковы, т.е. число молей при одинаковых параметрах идеальных газов прямо пропорционально полным объемам этих газов: Vi=Vi/Мi=Vсм/Мсм=Vсм.
Существует взаимосвязь массовых и объемных долей смеси. Ее несложно получить, выразив массы газов через произведение их объемов на плотности, а отношение плотностей при одинаковых параметрах, в соответствии с законом Авогадро, заменив отношением молекулярных масс:
 .
(3.76)
.
(3.76)
Уравнение (3.76) позволяет получить расчетные выражения для молярной массы и газовой постоянной смеси газов на основании равенства единице суммы массовых и объемных долей всех газов данной смеси:
 ,
,
 ,
,
 ,
(3.77)
,
(3.77)
 ,
,
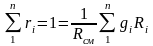 ,
,
 .
(3.78)
.
(3.78)
При известной молярной массе смеси газовую постоянную смеси проще определить из соотношения
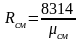 .
.
Для определения парциального давления данного газа в смеси можно воспользоваться выражением (3.71). В соответствии с ним
Pi = riPсм .
