
- •Введение техническая термодинамика как теоретическая основа теплоэнергетики
- •1. Общие определения и понятия
- •1.1. Термодинамическая система
- •1.2. Термодинамические параметры состояния
- •Основные термические параметры состояния
- •Удельный объем
- •Давление
- •Соотношения единиц измерения давления
- •Температура
- •1.3.2. Уравнение состояния термодинамической системы
- •1.3.3. Термические коэффициенты
- •1.3.4. Термодинамический процесс
- •2. Первый закон термодинамики для закрытой системы
- •2.1. Работа изменения объема
- •2.2. Теплота, теплоемкость, энтропия
- •2.3. Внутренняя энергия
- •2.4. Первый закон термодинамики для закрытой системы
- •2.4.1. Аналитические выражения первого закона термодинамики.
- •2.4.2. Энтальпия
- •3. Газы и газовые смеси
- •3.1. Законы идеальных газов
- •3.1.1. Внутренняя энергия идеального газа
- •3.1.2. Теплоемкости газов
- •Удельные теплоемкости
- •Теплоемкости процессов
- •Теплоемкости идеальных газов
- •Теплоемкость реальных газов
- •Отношение изобарной и изохорной теплоемкостей
- •3.1.3. Энтальпия идеальных газов
- •3.1.4. Энтропия идеальных газов
- •3.2. Газовые смеси
- •Основные характеристики смеси газов
- •Теплоемкости газовых смесей
- •4. Газовые процессы
- •4.1. Политропные процессы
- •4.2. Частные случаи политропных процессов
- •Уравнения процессов, расчетные выражения их теплоты, работы, изменения внутренней энерги, энтальпии и энтропи
- •4.3. Изображение политропных процессов в р,V и t,s- диаграммах Политропа в р,V- диаграмме
- •Политропа в t,s- диаграмме
- •4.4. Установление показателя политропы по опытным данным
- •4.5. Качественный и количественный анализ политропных процессов в р,V- и t,s- диаграммах
- •4.6. Определение термодинамических свойств идеальных газов с учетом влияния температуры на их изобарную и изохорную теплоемкости
- •Определение энергетических параметров идеальных газов с учетом влияния температуры на cp и cv
3.1.4. Энтропия идеальных газов
Для получения расчетного выражения изменения энтропии идеальных газов воспользуемся первым законом термодинамики, в котором теплота определяется с использованием изменения энтальпии:
 .
(3.58)
.
(3.58)
Для идеального газа изменение энтальпии определяется как dh=cpdT, а удельный объем v = RT/P. Подставив данные выражения изменения энтальпии и удельного объема в уравнение (3.58), получим уравнение для изменения энтропии идеального газа:
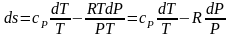 .
(3.59)
.
(3.59)
Разность энтропий идеального газа в конкретных точках можно получить интегрированием выражения (3.59):
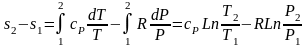 .
(3.60)
.
(3.60)
Воспользовавшись формулой Майера сp=сv+R и уравнением Менделеева – Клапейрона Pv=RT, выражение (3.60) можно записать и через две другие пары термических параметров состояния:
 .
(3.61)
.
(3.61)
Для определения абсолютного значения энтропии идеального газа необходимо зафиксировать начало ее отсчета любой парой термических параметров состояния. Например, приняв sо=0 при То и Ро, воспользовавшись уравнением (3.60), получим
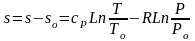 .
(3.62)
.
(3.62)
Выражение (3.62) свидетельствует о том, что энтропия идеального газа есть параметр состояния, поскольку ее можно определить через любую пару параметров состояния. В свою очередь, поскольку энтропия сама является параметром состояния, используя ее в паре с любым независимым параметом состояния, можно определить любой другой параметр состояния газа.
3.2. Газовые смеси
В практической деятельности чаще всего имеют дело не с однородными газами, а с их смесями (воздух, продукты сгорания топлива, горючие газовые смеси и т.п.). Поэтому в теплотехнике газовые смеси имеют важное значение.
В объеме, занимаемом газовой смесью, каждый газ, входящий в эту смесь, ведет себя так же, как вел бы себя при отсутствии других составляющих смеси: распространяется по всему объему; создает давление (парциальное), определяемое температурой и объемом на единицу его массы; имеет температуру смеси.
Смесь идеальных газов представляет собой идеальный газ, для которого справедливы законы и полученные для идеальных газов зависимости.
Для идеального газа давление определяется выражением (3.1):
.
Количество молекул, входящих в данную смесь газов, равно сумме молекул газов, составляющих смесь:
nсм = n1 + n2 + ··· + nn . (3.63)
Произведение mw2=2T пропорционально абсолютной температуре газа, а поскольку все газы, входящие в смесь, имеют одинаковую температуру, то справедливо равенство
2T = m1w12 = m2 w22 = ··· = mn wn2 . (3.64)
В соответствии с выражениями (3.63) и (3.64) давление для смеси газов можно представить в виде суммы

 ,
(3.65)
,
(3.65)
где Pi – парциальные давления газов, составляющих смесь.
Уравнение (3.65) представляет математическое выражение закона Дальтона (1807 г.) в соответствии с которым давление газовой смеси равно сумме парциальных давлений газов, входящих в смесь.
Парциальное давление – это давление, которое создает один из газов, составляющих смесь, при температуре смеси в случае заполнения им всего объема смеси. Парциальное давление – это реально-существующая величина, поскольку каждый отдельный газ в смеси имеет температуру смеси и занимает весь объем смеси. Парциальное давление можно определить из уравнения Менделеева –Клапейрона:
 ,
(3.66)
,
(3.66)
где Vсм – объем, занимаемый всей смесью газов;
mi – масса отдельного газа, входящего в смесь;
Ri– газовая постоянная отдельного газа;
Tсм – температура смеси газов.
