3.5 Знакоопределенные квадратичные формы. Критерий Сильвестра

Определение. Квадратичная форма называется положительно определенной, если для любого .

Квадратичная форма называется неотрицательно определенной, если для любого .

Квадратичная форма называется отрицательно определенной, если для всех .

Квадратичная форма называется неположительно определенной, если для всех .

Очевидно, что если – отрицательно (не положительно) определенная, то форма - – положительно (не отрицательно) определена, потому мы будем интересоваться условиями положительной и неотрицательной определенностей.

Квадратичная форма обладающая одним из перечисленых свойств, называется знакоопределенной в противном случае – знаконеопределенной.

Примеры.

1. – положительно определена в , т.к. для всех .

2. – не отрицательно определена в , т.к. , при-чем, на любом векторе , для которого .

3. – не является знакоопределенной, так при , а при .

Важно уметь определять “знак” формы. Не всегда это легко сделать по виду формы. Сформулируем без доказательства следующие теоремы.

Теорема 1. Квадратичная форма положительно определена тогда и только тогда, когда все собственные числа ее матрицы положительны.

Квадратичная форма неотрицательно определена тогда и только тогда, когда все собственные числа ее матрицы не отрицательны. Так например, квадратичная форма

положительно определена,

т.к. собственные числа ее матрицы положительны (см. пример 2, 1.2, гл. 1).

Другой способ определения “знака” квадратичной формы не требует вычисления корней характеристического многочлена. Дана матрица

.

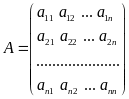Рассмотрим n ее миноров

,

,

,…,

.

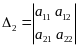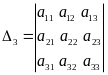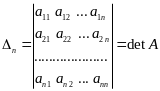Миноры будем называть угловыми минорами матрицы А.

Теорема 2. (Критерий Сильвестра). Квадратичная форма положительно опре-делена тогда и только тогда, когда все угловые миноры матрицы А положительны.

Пример 1. .

.

Угловые миноры: , , , 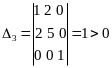следовательно, по критерию Сильвестра форма положительно определена.

Пример 2. .

.

Угловые миноры: , , .

Форма положительно определена.

Критерий Сильвестра не работает для выяснения неотрицательной определенности квадратичной формы.

Введем вспомогательные понятия. Определим главный минор порядка k матрицы А с помо-щью следующей процедуры:

– выбираем произвольные k элементов на главной диагонали;

– берем строки и столбцы, содержащие эти элементы;

– выписываем матрицу k-го порядка, элементы которой расположены на пересечении выделенных строк и столбцов. Определитель этой матрицы есть главный минор k-го порядка матрицы А, определяемый выбранным набором диагональных элементов.

Например, матрица 3-го порядка имеет

1) три главных минора 1-го порядка (диагональные элементы);

2) три главных минора 2-го порядка , , ;

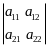3) один главный минор 3-го порядка – определитель матрицы .

Теорема 3. Квадратичная форма неотрицательно определена тогда, когда все главные миноры матрицы А неотрицательны.

Пример 3. .

.

Угловые миноры: , , .

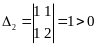По теореме 2 форма не является положительно определенной. Проверим знаки главных миноров матрицы А.

Главные миноры:

1) первого порядка: 1>0, 2>0, 2>0;

2) второго порядка: , , ;

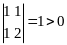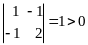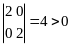3) минор третьего порядка: , следовательно, квадратичная форма неотрицательно определена.

В заключении покажем, как из критерия Сильвестра можно получить условие отрицательной определенности квадратичной формы. Пусть форма – отрицательно определена, тогда форма положительно определена, и угловые миноры матрицы –А положительны. Выпишем их для матрицы

, тогда .

Выпишем угловые миноры матрицы А:

;

;

.

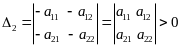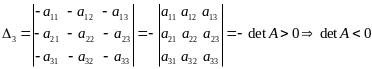Итак, квадратичная форма отрицательно определена, если знаки ее угловых миноров чередуются, причем первый из них ; ; ; и т.д.

Пример 4. .

;

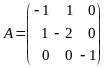угловые миноры: ; ; .

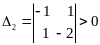Следовательно форма – отрицательно определена.