3 Система линейных уравнений
3.1 Основные определения и понятия
Рассмотрим систему m уравнений с n неизвестными
. (1)
Матрица A, составленная из коэффициентов при неизвестных системы, называется матрицей системы уравнений (1):
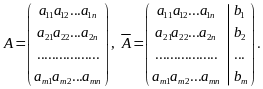
называют
расширенной
матрицей системы,
ее последний столбец отделяют вертикальной
чертой.
Векторы
и
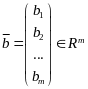
называют, соответственно, вектором неизвестных и вектором правых частей системы (1). В этих обозначениях векторно-матричная запись системы (1) выглядит так:
(2)
Если
вектор
,
то система
называется однородной,
если же
(хотя бы один из эле-ментов
отличен от нуля), то система
называется
неоднородной.
Решением
системы (1)
называется такой вектор
,
что при подстановке чисел
в систему (1) получаются верные равенства
(тождества).
Система, имеющая хотя бы одно решение, называется совместной, в противном случае – несовместной.
Две системы называются эквивалентными, если множества их решений совпадают. Если к некоторому уравнению системы прибавить другое, умноженное на число, то решения системы не меняются. Заметим, что операции над системой уравнений сводятся к элементарным преобразованиям над расширенной матрицей . Таким образом, элементарные преобразования над не меняют совокупности ее решений.
3.2 Однородные системы
Рассмотрим однородную систему
(3)
Заметим,
что однородная система всегда совместна,
поскольку нуль-вектор
– ее решение.
Вопрос лишь в том, единственно ли это решение и если нет, то что представляет собой совокупность всех ее решений.
Теорема.
Множество всех решений однородной
системы образует подпространство в
Действительно,
если
– решения системы (3), т.е.
и
,
то
,
где
– числа, также является решением системы
(3):
.
Итак, решения однородной системы можно складывать, умножать на число, новый вектор вновь будет решением этой системы. Мы знаем, что в любом подпространстве (кроме ) можно выделить базис и любой вектор подпространства представить в виде линейной комбинации векто-ров базиса.
Обозначим
V
– подпространство решений однородной
системы (3), а
– некоторый базис в V.
Любой базис подпространства V решений однородной системы называют фундаментальной системой решений (ФСР).
Число
векторов ФСР
,
где
– число неизвестных системы (3), а r
– ранг матрицы A.
Таким образом, размерность подпространства
решений
.
Любой
вектор-решение
(общее решение) является линейной
комбинацией векторов ФСР:
.
Научимся находить общее решение однородной системы. Для этого применяется метод Гаусса. Метод Гаусса для решения систем уравнений состоит из прямого и обратного хода. Прямым ходом заданную систему приводят к эквивалентной ступенчатой системе, которая легко поддается исследованию. Решение системы находится обратным ходом метода Гаусса.
Проиллюстрируем алгоритм метода на примере системы:
.
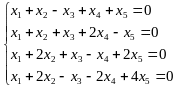Все преобразования системы сводятся к преобразованиям матрицы системы.
Прямой ход метода Гаусса
1. Приведем матрицы системы к ступенчатому виду:
.
Матрица
Р
ступенчатая, ее ранг
.
2. Выпишем соответствующую систему уравнений:
.
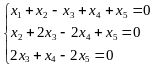Мы
отбросили последнее уравнение, все
коэффициенты которого равны нулю.
Заметим, что угловые элементы матрицы
Р
являются коэффициентами при
в ступенчатой системе.
3.
Назовем переменные
,
не связанные с угловыми элементами,
свободными,
а
– зависимыми
переменными
(несвободными).
Зависимыми переменными всегда объявляются
переменные, коэффициентами которых
являются угловые элементы. Заметим, что
при другом способе приведения матрицы
к ступенчатому виду свободными переменными
могут оказаться переменные с другими
индексами. Однако число свободных
переменных всегда равно
В данном примере
Обратный ход метода Гаусса
1. Выразим зависимые переменные через свободные из ступенчатой системы, начиная с пос-леднего уравнения и «поднимаясь» вверх к первому. В результате получим
.
(*)
Полученные выражения дают описание всего множества решений однородной системы (3). Давая свободным переменным произвольные значения (они играют роль параметров для множест-ва решений) и вычисляя значения зависимых переменных, получаем некоторое частное решение системы. Так можно получить все решения системы, поэтому выражения (*) называют общим решением системы в координатной форме.
2.
Запишем общее решение в векторной форме.
Выберем из общего решения (*)
линейно независимых решений и составим
из них ФСР. Для этого придадим свободным
перемен-ным значения
,
тогда из (*)
получим
и
;
затем
,
вычислим из (*)
и
.
Векторы
линейно независимы (в силу выбора
свободных переменных) и образуют ФСР.
Общее решение системы, записанное в векторной форме, имеет вид
.
Итак,
размерность подпространства
есть
,
где
.
Если
(т.е. A
имеет «полный ранг»),
,
т.е.
имеет нулевую
размерность (
),
а значит, состоит лишь из нулевого
вектора
.
В этом случае однородная система имеет
единственное нулевое (тривиальное)
решение.