Тематический обзор*

1 Арифметическое линейное пространство Rn

1.1 Основные понятия и определения

При изучении векторной алгебры мы видели, что если в трехмерном пространстве ввести систему координат, то векторы однозначно представляются тройками чисел

и операции над векторами сводятся к соответствующим операциям над тройками чисел. Во мно-гих вопросах математики и ее приложений приходится иметь дело не с тройками, а с четверками, пятерками и т.д. действительных чисел. Например, если предприятие выпускает n видов продукции в количествах единиц, соответственно, то весь выпуск (за некоторый промежуток времени) определяется набором

из n действительных чисел.

Такие упорядоченные наборы из n чисел мы будем по-прежнему называть векторами или n-мерными векторами. Числа называются компонентами вектора .

Символом Rⁿ обозначается множество, рассматриваемое вместе с операциями сложения и умножения на числа, элементами которого являются n-мерные векторы.

1. Пусть – два вектора из множества Rⁿ. Их суммой называется вектор , который по определению равен .

2. Операция умножения вектора на число определяется так: произведением вектора на число называется вектор такой, что .

Итак, операции сложения и умножения на скаляр определяются покоординатно (покомпонентно).

Определение. Множество Rⁿ векторов с покомпонентным сложением и умножением на число называется n-мерным арифметическим линейным (векторным) прост-ранством Rⁿ.

Вектор называется нулевым ( -вектор) вектором. Для каждого вектора существует противоположный вектор . Так как операции над векто-рами в пространстве Rⁿ сводятся к операциям над числами (их компонентами), то легко проверить, что выполняются следующие свойства сложения и умножения на число:

а)

б)

в)

г)

д) – числа.

Два вектора и равны тогда и только тогда, когда их одноименные компоненты совпадают. Примерами арифметических пространств служат уже знакомые нам пространства , элементами которого являются векторы на плоскости, и - пространство трехмерных векторов, заданных своими координатами. Вектор является коллинеарным вектору , а -вектор геометрически изображается точкой.

Определение. Линейной комбинацией векторов с коэффициентами называется вектор .

Определение. Совокупность всех линейных комбинаций векторов называется их линейной оболочкой.

Векторы можно представить в виде строк или столбцов (соответственно, говорят о век-торах-строках и векторах-столбцах).

1.2 Линейная независимость. Базис в пространстве Rn

Пусть имеются два вектора и в и пусть . Такие векторы в и мы называем коллинеарными, т.е. вектор получается из вектора умножением на число . Или рассмотрим такую тройку векторов , что ( - числа), т.е. есть линейная комбинация векторов и ; в рассмотренных случаях говорят, что векторы представляют систему линейно зависимых векторов.

Определение. Система векторов называется линейно зависимой, если один из векторов этой системы является линейной комбинацией остальных (линейно выражается через остальные).

Линейная независимость определяется как отрицание линейной зависимости: система векто-ров считается линейно независимой, если ни один из векторов этой системы не может быть выражен через остальные.

Дадим еще одно, эквивалентное, определение линейной независимости системы векторов.

Определение. Система векторов называется линейно независимой, если из ра-венства нулевому вектору линейной комбинации этих векторов выте-кает, что все коэффициенты этой линейной комбинации равны нулю: .

Линейная комбинация с нулевыми коэффициентами называется тривиальной. Таким образом, линейная независимость означает, что никакая нетривиальная линейная комбинация не равна ну-левому вектору, нулевой может быть лишь тривиальная комбинация системы линейно незави-симых векторов.

Так, в пространстве любая пара ненулевых векторов линейно независима тогда и только тогда, когда (векторы неколлинеарны), а любые три вектора на плоскости образуют линейно зависимую систему. В трехмерном пространстве векторов система векторов линейно независима тогда и только тогда, когда эти векторы не лежат в одной плоскости (некомпланарны).

Утверждение. Всякая система векторов, содержащая 0-вектор, линейно зависима. Особую роль среди линейно независимых систем играют системы, называемые базисом.

Определение. Базисом линейного пространства Rⁿ называется система векторов , удовлетворяющая требованиям:

1) векторы линейно независимы;

2) любой вектор является линейной комбинацией векторов , где – числа;

3) число векторов системы равно n.

Можно показать, что выполнение любой пары из перечисленных условий гарантирует справедливость третьего условия.

Пример. В известные нам векторы обладают требуемыми свойствами и образуют базис в пространстве. Базис обладает дополнительными свойствами – векторы базиса взаимно ортогональны, их длины равны 1. Такой базис называют ортонормированным.

Аналогичный базис можно предъявить в пространстве . Покажем, что система векторов , где

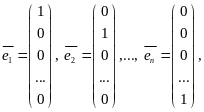
образует базис в .

1. Проверим линейную независимость этих векторов. Составим их линейную комбинацию и приравняем ее :

Распишем это векторное равенство покоординатно:

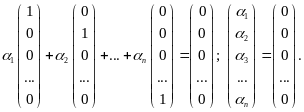
Мы воспользовались правилами умножения вектора на число и сложения векторов. Получили , отсюда следует линейная независимость .

2. Разложение произвольного вектора из по векторам выглядит особенно просто: .

Базис называют стандартным или каноническим.

Отметим, что предъявленный базис не единственный в , любая линейно независимая система из векторов образует базис в .

Разложение вектора по данному базису единственно.

Коэффициенты в разложении вектора по базису называются координатами вектора в базисе .

Подчеркнем, что число векторов во всех базисах равно n, это общее число векторов базиса пространства называется размерностью пространства: (от слова dimension).

Максимальное число r линейно независимых векторов системы называется рангом (rang) системы векторов.