1.1.4. Механические колебания

Уравнение гармонических колебаний –

,

где x – смещение колеблющейся точки от положения равновесия; A, ω, φ – соответственно амплитуда, круговая (циклическая) частота, начальная фаза колебаний; t – время; – фаза колебаний в момент t.

Круговая частота колебаний –

, или ,

где  и T – частота и период колебаний.

Скорость точки, совершающей гармонические колебания, –

.

Ускорение при гармоническом колебании –

.

Амплитуда А результирующего колебания, полученного при сложении двух, происходящих вдоль одной прямой, колебаний с одинаковыми частотами, определяется по формуле

,

где и – амплитуды составляющих колебаний; и – их начальные фазы.

Начальная фаза φ результирующего колебания может быть найдена из формулы

.

Частота биений колебаний, возникающих при сложении двух колебаний, происходящих вдоль одной прямой с различными, но близкими по значению частотами и , –

.

Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях с амплитудами и и начальными фазами и , –

,

т.е. точка движется по эллипсу.

Дифференциальное уравнение гармонических колебаний материальной точки :

, или ,

где m – масса точки; k – коэффициент квазиупругой силы .

Полная энергия материальной точки, совершающей гармонические колебания, –

.

Период колебаний тела, подвешенного на пружине (пружинный маятник), –

,

где m – масса тела; k – жёсткость пружины.

Формула справедлива для упругих колебаний в пределах, в которых выполняется закон Гука (при малой массе пружины в сравнении с массой тела).

Период колебаний математического маятника

,

где – длина маятника; g – ускорение свободного падения.

Период колебаний физического маятника –

,

где – приведённая длина физического маятника; J – момент инерции колеблющегося тела относительно оси колебаний; a – расстояние от центра масс маятника до оси колебаний.

Эти формулы являются точными для случая бесконечно малых амплитуд. При конечных значениях они дают лишь приближенные результаты. При амплитудах не более ~ 3⁰ погрешность в значении периода не превышает 1%.

Период крутильных колебаний тела, подвешенного на упругой нити, –

,

где J – момент инерции тела относительно оси, совпадающей с упругой нитью; k – жесткость упругой нити, равная отношению упругого момента, возникающего при закручивании нити, к углу, на который нить закручивается.

Дифференциальное уравнение затухающих колебаний :

, или ,

где r – коэффициент сопротивления; δ – коэффициент затухания, ;

- собственная круговая частота колебаний, .

Решение дифференциального уравнения затухающих колебаний –

,

где А(t) – амплитуда затухающих колебаний в момент времени t;  - круговая частота затухающих колебаний в момент t.

Круговая частота затухающих колебаний –

Зависимость амплитуды затухающих колебаний от времени –

,

где - амплитуда колебаний в момент t=0.

Логарифмический декремент затуханий :

,

где A(t) и A(t+T) – амплитуды двух последовательных колебаний, отстоящих по времени друг от друга на период.

Дифференциальное уравнение вынужденных колебаний :

, или ,

где – внешняя периодическая сила, действующая на колеблющуюся материальную точку и вызывающая вынужденные колебания; – её амплитудное значение, .

Амплитуда вынужденных колебаний :

.

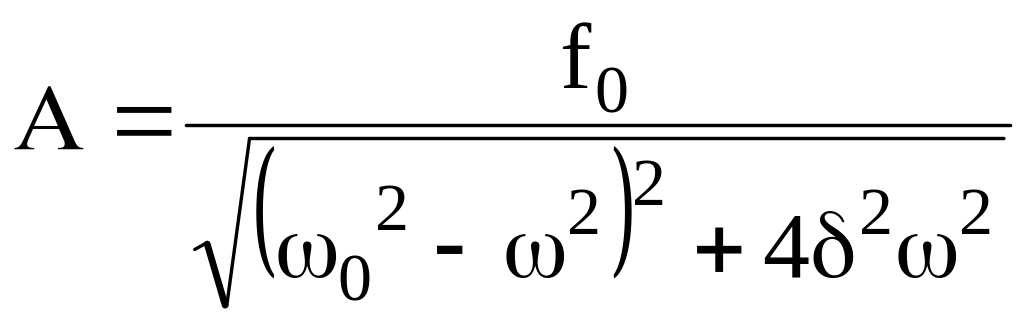Резонансная частота и резонансная амплитуда :

и .
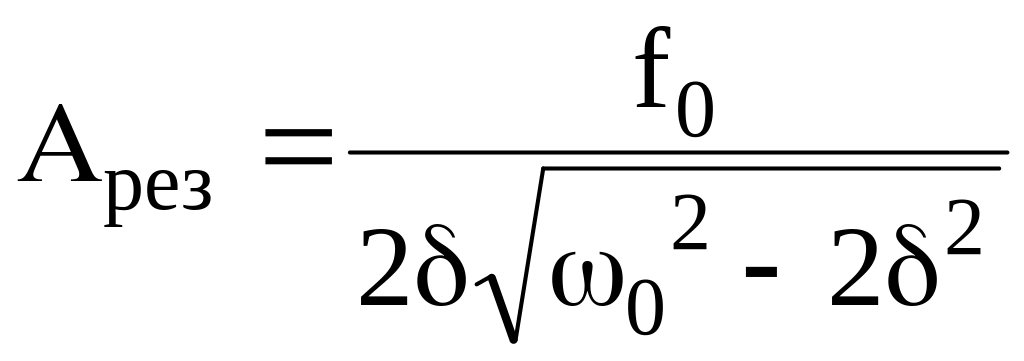