3. Критерий Найквиста

Он используется для цепей с явной обратной связью.

Когда при какой-то частоте , то цепь неустойчива, так как в этом случае на вход подается все время увеличивающийся сигнал и при этом в той же фазе (переходный процесс возрастающий). Произведение называют петлевым усилением. Рассматривают цепь с разомкнутой обратной связью, но нагруженной на входное сопротивление, что бы не изменились коэффициенты передачи.

Получаем, что цепь устойчива, когда петлевое усиление не превышает единицы.

Е сли К▪β=1 (К▪β=1и φ_К+φ_β=0), то К_ОС=∞, то есть на выходе есть сигнал U₂, когда на входе сигнал U₁=0.(U₂/0=∞).

Для применения критерия используют годограф петлевого усиления, построенный при изменении частоты от 0 до ∞ .

Для устойчивой цепи годограф петлевого усиления не должен охватывать точку с координатами (1;j0) при изменении частоты от 0 до ∞. На рисунке показан примеры годографов устойчивой цепи.

7.7. Автоколебательные цепи или автогенераторы

Автогенераторы – это такие устройства, которые без внешнего гармонического воздействия вырабатывают колебания какой-то формы (в частности, гармонической). В принципе в них должны быть источники питания (постоянного напряжения или тока), нелинейные элементы и положительная обратная связь (в явной или неявной форме).

Р ассмотрим структуру автоколебательной цепи с явной обратной связью и усилителем.

Рассмотрим петлевое усиление. Если на какой-то частоте, то цепь будет неустойчивой и, автогенератор будет вырабатывать гармонические колебания.

- это баланс амплитуд и баланс фаз, ω_Г - частота генерации.

Сам усилитель и обратная связь должны быть по отдельности устойчивы, а вместе – неустойчивы.

Для того, чтобы было возбуждение, необходимо, чтобы петлевое усиление немного превышало 1. В простейшем случае усилитель – это ИНУН, в котором коэффициент управления превышает единицу, т.е. это частотно независимая цепь.

Цепь обратной связи (ЦОС) обычно частотно-зависимая цепь (содержит индуктивности, емкости). По типу элементов разделяют RC-автогенераторы, LC-автогенераторы, транзисторные автогенераторы, автогенераторы на операционных усилителях. Могут быть генераторы на специальных диодах (туннельных), но это генераторы с внутренней обратной связью.

7.8. RC-автогенераторы

Рассмотрим RC-автогенератор на операционном усилителе.

Вход с минуса ОУ называется инвертирующим (здесь фаза изменяется на 180⁰).

У идеального ОУ входное сопротивление бесконечно велико, а выходное равно 0.

Схема замещения идеального ОУ выглядит следующим образом:

Для идеального ОУ μ→∞.

Р ассмотрим усилитель автогенератора

Коэффициент усиления по напряжению усилителя генератора для случая идеального ОУ определяется формулой:

K=U₂/U₁ ≈ (R3+R4)/R3 .

Для реального ОУ следует учитывать входные и выходные сопротивления, емкости и конечность коэффициента усиления по схеме замещения конкретного типа ОУ.

Р ассмотрим цепь обратной связи этого автогенератора

Коэффициент передачи ЦОС определяется выражением: (в режиме холостого хода).

Для усилителя с идеальным ОУ входное сопротивление будет равно ∞.

Отсюда можно получить формулу .

При C₁=C₂=C и R₁=R₂=R получим

Общий коэффициент передачи автоколебательной цепи с учетом обратной связи равен: . Так как используемый усилитель не сдвигает фазу, то и ЦОС не должна сдвигать ее, чтобы выполнялось условие баланса фаз. Для этого, поскольку числитель вещественен, мнимая часть знаменателя должна равняться 0. Отсюда получим частоту генерации (возбуждения) При этом β(ω_Г)=1/3 и для баланса амплитуд К=3 (>3).

Примерные частотные характеристики ЦОС приведены далее при использовании ω=2πf.

β(0)=0, β(∞)=0.

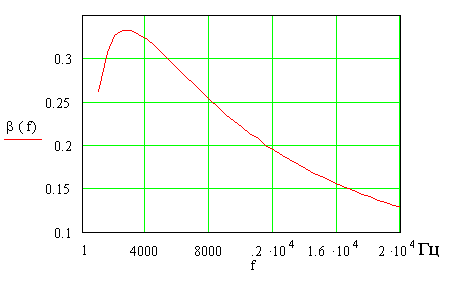
Возбуждение генератора показано далее

З десь видно, что колебания не совсем гармонические. Это недостатки RC генераторов, достоинство в том, что тут нет индуктивностей.

Рассмотрим транзисторный RC-автогенератор.

б

Сдвиг фаз в транзисторном усилителе .(когда напряжение на входе увеличивается, увеличивается коллекторный ток транзистора и увеличивается напряжение на R_K, но при этом уменьшается выходное напряжение).

Для получения такого же сдвига фаз в ЦОС необходимы 3 RC-цепочки (одна дает сдвиг фаз меньше π/2), тогда общий сдвиг фаз будет 0 или 2π. Тройная RC-цепочка ослабит входное напряжение примерно в 27 раз. Следовательно усилитель должен иметь усиление не менее 27 раз. Для точных расчетов надо составить схему замещения такой цепи с учетом схемы замещения транзистора в соответствующем диапазоне частот.

7.9. LC-автогенераторы

В них используется колебательный контур и обратная связь через трансформатор или взаимную индуктивность.

L C

Напряжение смещения выбирают таким образом, чтобы установить рабочую точку транзистора в середине линейного участка. Схема замещения контура с учетом влияния обратной связи:

Здесь: G_oc – проводимость обратной связи, G_кон – проводимость контура, i_k – коллекторный ток.

Составим уравнение по первому закону Кирхгофа для узла (1):

. Поменяв знаки и выразив токи через напряжение контура получим:

Поделим на С и продифференцируем, а затем составим характеристическое уравнение:

. Для получения незатухающего (возрастающего) переходного процесса корни должны быть комплексно сопряженными с положительной вещественной частью. Для этого и тогда

График зависимости i_k(u_бэ) характеризуется величиной крутизны S.

, , где – резонансное сопротивление параллельного контура , а R_k – сопротивление катушки индуктивности.

Определим М_крит:

Частота генератора равна частоте свободных колебаний контура и при резонансной частоте колебаний контура.

7.10. LC-автогенераторы с внутренней обратной связью

Используется специальный диод, например, туннельный, и колебательный контур.

У туннельного диода специфическая ВАХ:

0 U_СМ

I_ТД

Туннельный диод можно характеризовать некоторой отрицательной дифференциальной проводимостью при соответствующем смещении (U_СМ). Необходимое смещение достигается подбором величины сопротивления резистора R .

Схема замещения похожа на схему замещения транзисторного LC-автогенератора.

Условие колебаний: .

Дифференциальная проводимость туннельного диода должна компенсировать потери в контуре. Частота возбуждения (генерации) будет равна резонансной частоте контура.

97