37

ОГЛАВЛЕНИЕ

4

Общие сведения об управлении. 4

1.Цели управленияя. 4

2. Типовые законы регулирования 5

3. Типовые законы регулирования по отклонению 7

4. Классификация систем управления 10

5. Общие сведения о моделях систем. 11

Модели элементов САР 11

6. Уравнения элементов САУ 12

7. Линеаризация на основе гипотезы о малых отклонениях 13

8. Преобразование Лапласа 15

9. Передаточные функции элемента 17

Структурные схемы элементов. 18

10. Правила преобразования структурных схем. 18

11. САР двигателя постоянного тока. 20

12. Передаточная функция замкнутой системы 21

Характеристики системы. 22

13. Общие сведения о характеристиках. 22

14. Переходная характеристика 23

15. Импульсная переходная характеристика 23

23

16. Замкнутая система.Передаточные функции 24

17. Определение реакции системы на произвольный входной сигнал во временной области 25

18. Основные свойства импульсных переходных характеристик 25

19. Частотные характеристики 26

20. Логарифмические частотные характеристики 30

21. Логарифмические характеристики разомкнутой одноконтурной системы. 31

Звенья САР. 39

23. Понятие о звене. 39

24. Усилительное звено 40

. 40

27. Колебательное звено 43

ДУ звена . 43

28. Консервативное звено. 45

29. Идеальное дифференцирующееиальное звено. 47

30. Идеальное интегрирующее звено. 48

31. Звено запаздывания 49

я. 49

32. Неустойчивое звено 1-го порядка. 50

Анализ систем. 51

33. Анализ устойчивости. 51

34. Исследование устойчивости линеаризованных систем 52

35. Критерии устойчивости. 54

36. Запасы устойчивости 59

37. Анализ влияния коэффициента усиления разомкнутой системы на устойчивость замкнутой системы. 61

38. Логарифмический критерий устойчивости 62

39. Определение устойчивости при описании систем в пространстве состояний. 63

40. Матричный критерий Зубова. 64

Анализ точности в установившихся режимах. 66

41. Общие сведения об анализе точности 66

42. Полиномиальные сигналы. 67

43. Особенности анализа ошибки по возмущению. 68

Медленно меняющиеся сигналы. 69

44. Коэффициенты ошибок. 69

45. Анализ точности при гармонических сигналах 71

46. Анализ точности при сигналах, ограниченных по скорости и ускорению. 71

47. Пути повышения точности системы в установившихся режимах 71

48. Анализ качества переходных процессов 75

49. Показатели качества переходного процесса, определяемые по переходной характеристике. 76

50. Прямые методы. 77

51. Косвенные методы. 77

52. Оценка показателей качества по корням. 78

53. Оценка показателей качества по АЧХ замкнутой системы. 78

54. Оценка показателей качества по ЛАЧХ разомкнутой системы. 79

55. Интегральные оценки качества 80

Чувствительность систем. 83

56. Функции чувствительности. 83

Коррекция систем. 84

57. Общие сведения о коррекции. 84

58. Последовательная коррекция 85

59. Параллельная коррекция 87

60. О модальном регулировании 89

Дискретные системы 90

61. Общие сведения о дискретных системах 90

62. Разностные уравнения 91

63. Z – Преобразование. 91

Передаточные функции дискретных систем. 93

64. Передаточная функция дискретного фильтра. 93

65. Передаточная функция формирователя импульсов и объекта. 93

66. Передаточная функция объекта, описанного уравнениями состояния при кусочно-постоянном уравнении. 95

67. Устойчивость дискретных систем. 95

68. Анализ качества дискретных систем. 97

69. Анализ ошибок воспроизведения входных сигналов. 98

70. Типовые законы регулирования, реализующиеся цифровыми регуляторами. 100

71. Анализ качества переходных процессов дискретных систем. 101

72. Пример определения ПХ. 102

Литература: 104

Общие сведения об управлении

1.Цели управления

Использование термина управление предполагает наличие технического устройства, которое выполняет полезную работу. Эта работа может быть произведена в короткий или длительный промежуток времени. ТАУ изучает системы, которые осуществляют работу на длительном интервале времени. Любое техническое устройство, выполняющее полезную работу это объект(O). При описании объекта интересуются:

1) выходом объекта – полезная работа y(t);

2 ) управляющим воздействием –u (t) , которое способно направить y(t) в нужное русло.

Любой объект находиться под действием внешней среды, которая неблагоприятно воздействует на него возмущениями F(t). Эти возмущения могут быть как внешними, так и внутренними. Bоздействия рассматриваются как функции времени

y(t), t Є [t₀,∞] u(t), t Є [t₀,∞] , F(t), t Є [t₀,∞],

t₀– время, относительно которого учитывается эффект управления (начальный момент времени). Если объект существенно не меняет своих свойств в начале управления то t₀=0, то объект называют стационарным. Если t₀ обнулить нельзя, то объект называют нестационарным.

В зависимости от сложности объекта можно выделить объекты скалярные (одномерные) и многомерные с векторным описанием сигналов:

; ; , t Є [0,∞]

Д ля управления объектом нужна цель управления. Цель определяет, что y(t)→ Y_ж(t) (желаемое).Вид Y_ж (t) определяется лицом, принимающим решения (ЛПР). Выработка требуемого управления объектом позволяет достигать поставленную цель. Выработку такого управления осуществляет устройство управления (УУ).

Взаимодействие этих трёх компонентов образует систему управления,

где V(t) – входной сигнал системы , поступающий с более высокого уровня управления,

В задачу УУ входят выработка цели управления. Цели управления на ранних этапах были простыми. Y_ж(t)=const, Y_ж (t)→ Y (t) – известная функция времени. В дальнейшем Y_ж (t) стали подавать как входные сигналы системы управления V(t)= =Y_ж(t) , и появились системы автоматического регулирования (САР).

В зависимости от реализации УУ различают следующие системы управления:

1. Система ручного управления. В качестве устройства управления в таких системах используется человек-оператор. Оператор реализует управление со сложными целями, принимая решения, вырабатывает U(t), способное достичь поставленную цель.

2. Система автоматического управления (САУ). В качестве УУ используют автомат. Применяется при :

а) управлении в опасных для жизни и здоровья человека условиях;

б) быстродействие управляемых процессов слишком велико для человека;

в) работа управления носит монотонный (нудный) характер.

3 . Автоматизированная система управления. В ней в качестве УУ используют как человека, так и автомат. В данных системах человек занимается анализом ситуации и выработкой цели, а автомат реализует управление, заданное человеком, и собирает (а также представляет в удобном виде) для него необходимую информацию.

Наиболее простая система управления это САР. Рассмотрим процесс регулирования с простой целью. При этом используется следующая модель:

Р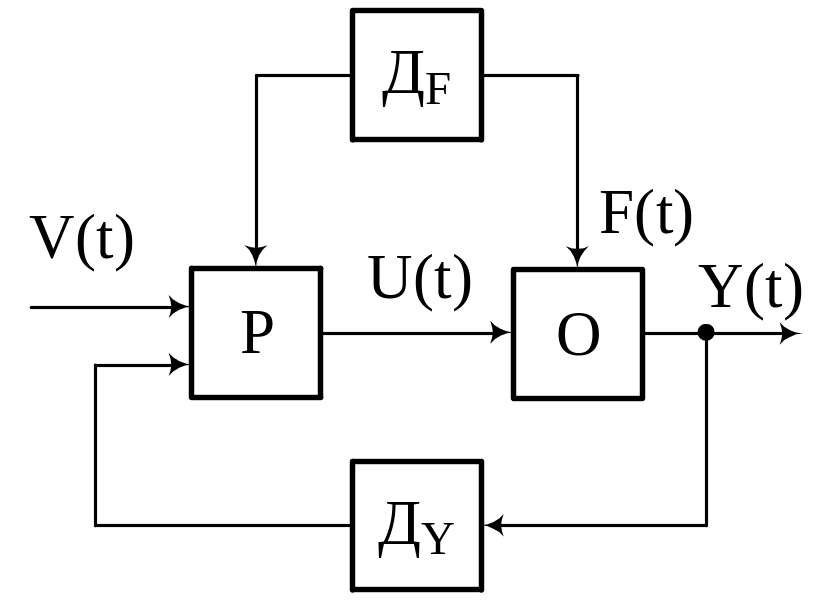 – регулятор предназначен для выработки сигнала управления в виде U=O*(V,Y,F) – способeн вырабатывать требуемое управление. О– оператор объекта;

Y→Дy – датчик выходного сигнала;

F→Дf – датчик возмущения действующего на объект (чаще всего оно не измеримо).

2. Типовые законы регулирования

Типовые законы регулирования могут быть рассмотрены сначала как принципы построения САР.

1. Р азомкнутый принцип

Значение регулирования определяется выражением: U=P(V) , V=Y_ж; если обозначить оператор объекта O то U=P(V)=O^-1(Y_ж). Основными недостатками такой системы являются:

a) не учитывает действие внешних возмущений;

б) не учитывает действие внутренних возмущений, изменяющих характеристики объекта и УУ.

П римером такой системы служит система управления шаговым двигателем.

2. Управление по возмущению

Д f– датчик внешних возмущений на О. Управление определяется выражением: U=P(V,F). По входному сигналу управление V→Y - разомкнутое.

3. Замкнутое управление. Управление

с обратной связью

.

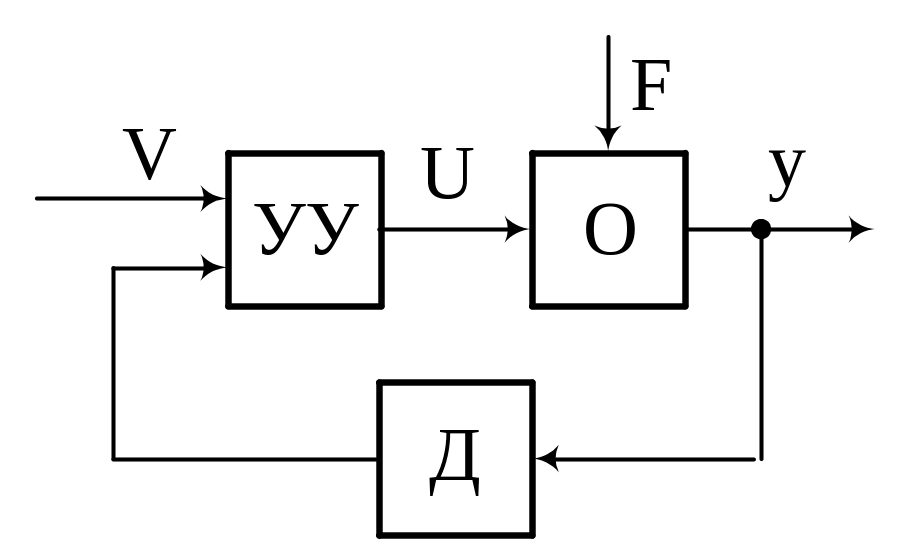
Д – датчик измерения и преобразования выходного сигнала. Управление определяется выражением: U=P(V,y), V→y_ж. При этом, сравнивая V и y, можно говорить об ошибке

Е=V-y.

Регулирование по отклонению (ошибке) осуществляется с использованием сравнивающиx устройств (сумматоров). На схемах сумматоры обозначаются в видах:

С их использованием схема будет иметь вид: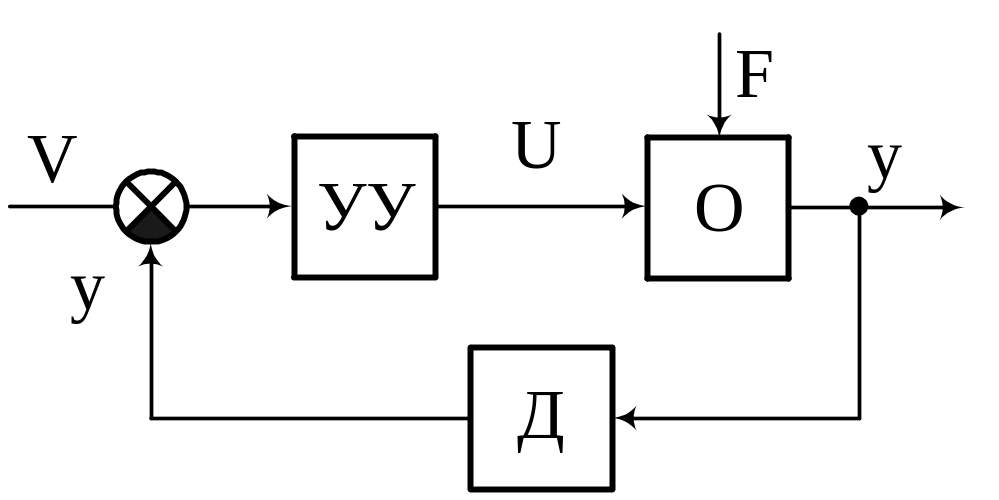

E =V–y→0. Уравнения с такой постой целью называют регулирующим. УУ – является регулятора. Датчик на схема можно не обозначать:

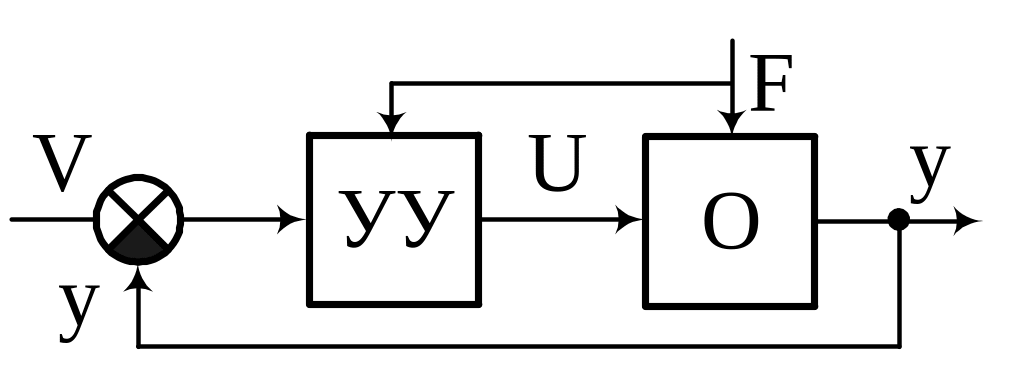3. Комбинированное управление. Совмещение замкнутого управления и управления по возмущению.

Применимо в тех случаях, когда требуется высокоточное управление и имеется возможность измерять F.

Достоинства: замкнутое управление позволяет реагировать на любые отклонения у как от V так и от F.

4. Управление с поиском экстремума.

Объект управления может иметь многоэкстремальную характеристику. V=V₁+V₂, где V₁– быстро, а V₂– медленно меняющийся процесс. V₁ позволяет находит экстремум.

5. Оптимальное управление

Качество зависит от нескольких факторов: Q=Q(V,y,U), где UЄ u – множество допустимых управлений, V – цель управления, yЄ Y–(множество допустимых выходов).

U * : Q→ extr, при котором UЄ u. Цель управления – нахождение при заданных ограничениях.

6 Адаптивное управление. Сводится к выработке таких управлений, которые наиболее адекватно соответствуют меняющимся условиям и целям управления. Адаптация множество осуществляться как с изменением параметров системы без изменения структуры УУ, так и с изменением структуры и параметров системы. При этом естественно должны быть предусмотрены контуры изменения параметров и структуры. УУ (устройство управления), О (объект) и ВУ (вычислитель параметров) образуют контур изменения структуры и параметров системы.

3. Типовые законы регулирования по отклонению

1.Пропорциональный закон (П – закон).

U=Kp∙E ,

где Kp – коэффициент усиления регулятора. Регулятор представляет собой безынерционный усилитель (Е_ср→ U_ср). Данный закон ещё называется также статическим.

Достоинства:

Простота системы. Высокое быстродействие.

Недостатки:

В установившемся режиме имеется не нулевая ошибка (статическая ошибка).

y_ж → y₀ , а для этого U₀=const, а значит E₀=U₀/Kp≠0.

1. Интегральный закон (И – закон).

,

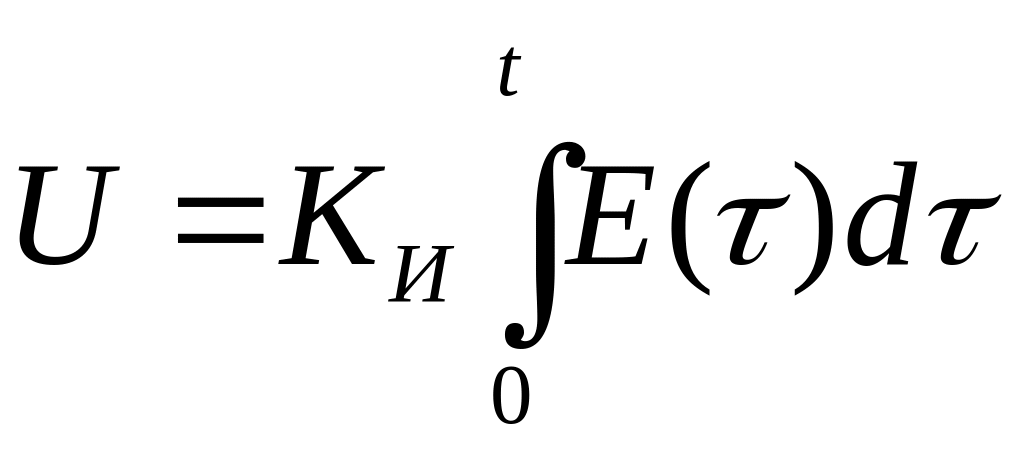где Ки=1/Tи – коэффициент усиления.

При t>t0 E(t)=0. Это значит что

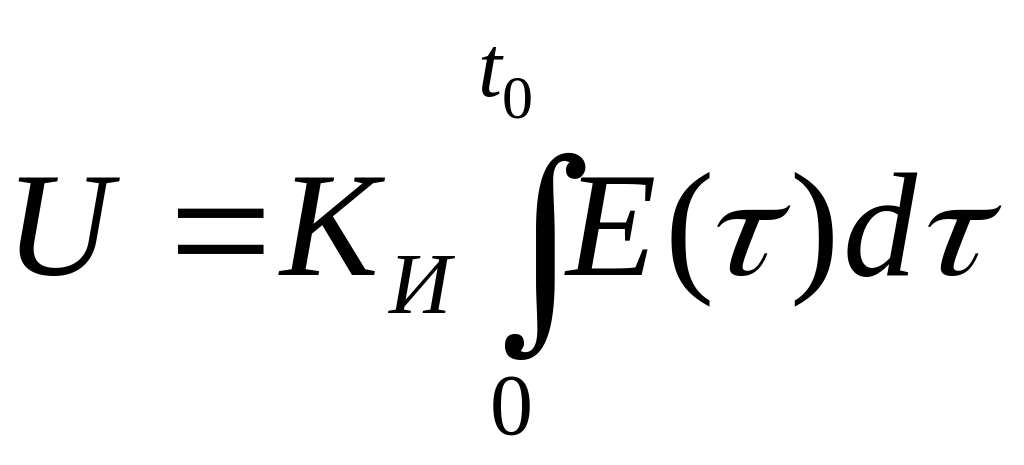
Достоинства:

Отсутствует статическая ошибка E₀= 0.

Недостатки:

Медленное быстродействие, большая инерционность.

2. Пропорционально - интегральный закон (ПИ – закон).

,

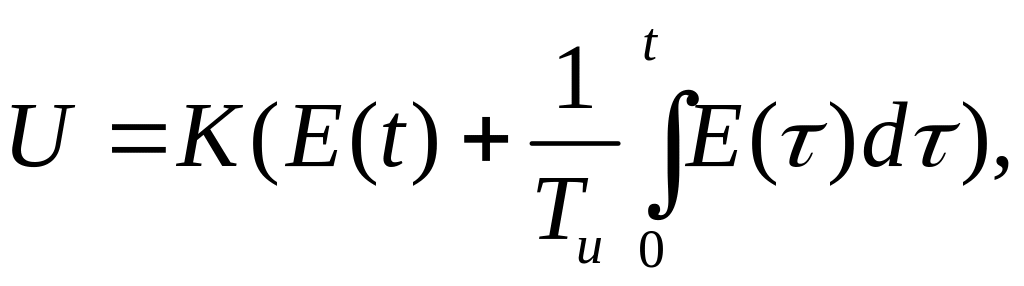где K, Tи, – коэффициент усиления и постоянная времени.

Достоинства:

Позволяет комбинировать астатизм И - закона, и быстродействие П - закона.

Недостатки:

Иногда не может обеспечить необходимое быстродействие.

3. Пропорционально - интегрально - дифференциальный закон (ПИД – закон).

,

где T - постоянная времени дифференцирования. Ки, Кп – коэффициенты усиления от П и И законов.

Достоинства:

Последняя составляющая обеспечивает управление при увеличении скорости возрастания ошибки, позволяя уменьшить её размер.

4. Пропорционально - дифференциальный закон (ПД – закон).

,

где T_д- постоянная времени дифференцирования.

Эти законы являются линейными законами регулирования. Регулятор реализующие эти законы называются аналогично (П - регулятор, И -регулятор и т.д.). Для их реализации на аналоговых элементах требуется ОУ. Учитывая продолжительность работы ориентироваться на ОУ не всегда возможно.

В некоторых случаях целесообразно использовать нелинейные законы. Они позволяют получать свойства системы более предпочтительные по сравнению с линейной зависимостью. Типовые нелинейные законы принято описывать характеристиками нелинейных элементов.

1. Характеристика идеального реле

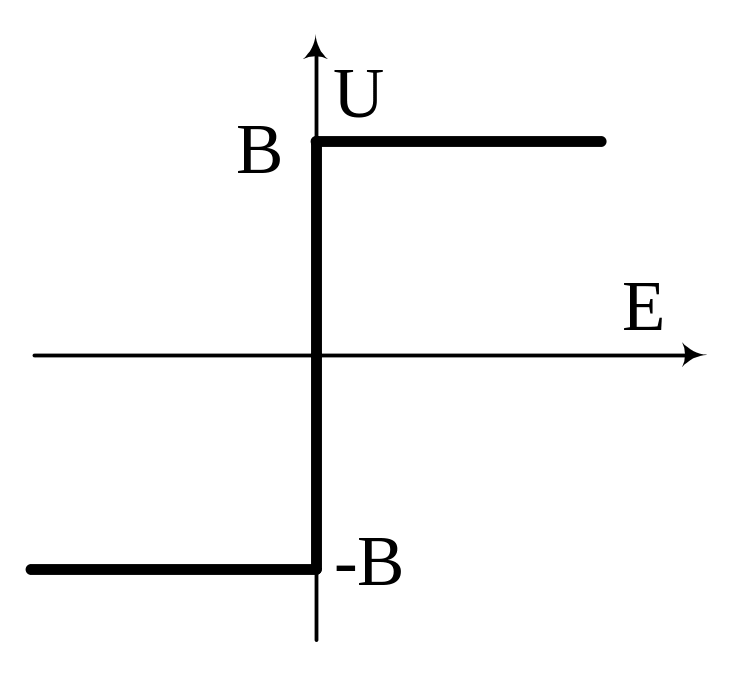
U=B∙sgn(E), где sgn(E)= E/|E|

2. Реле с зоной нечувствительности

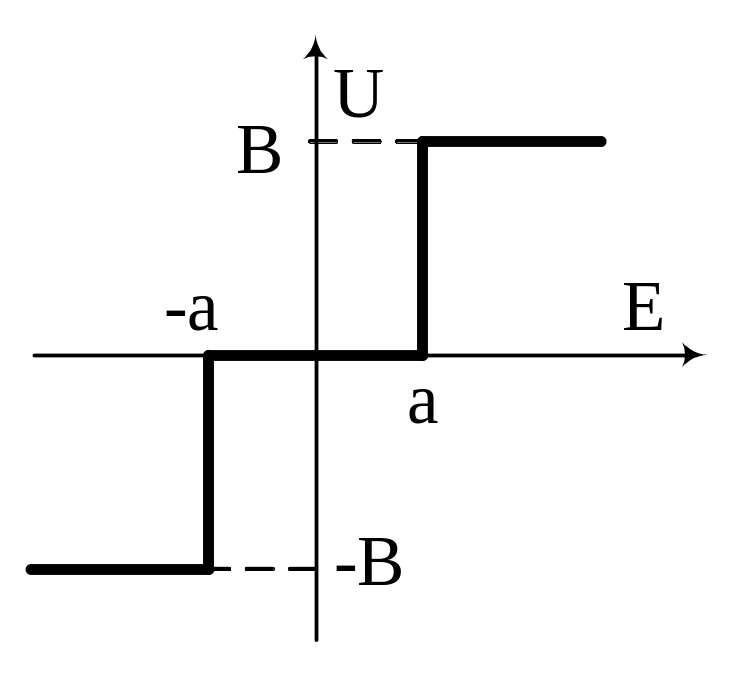
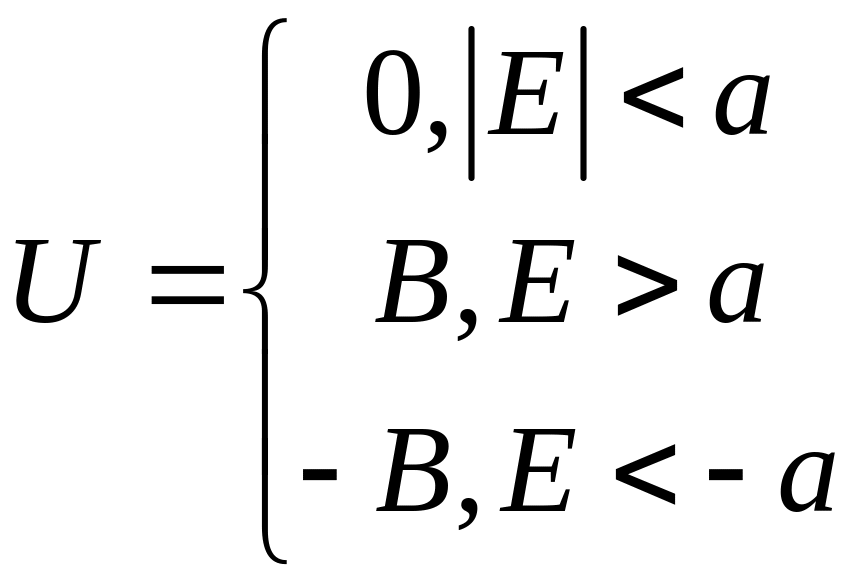
3. Реле с гистерезисом

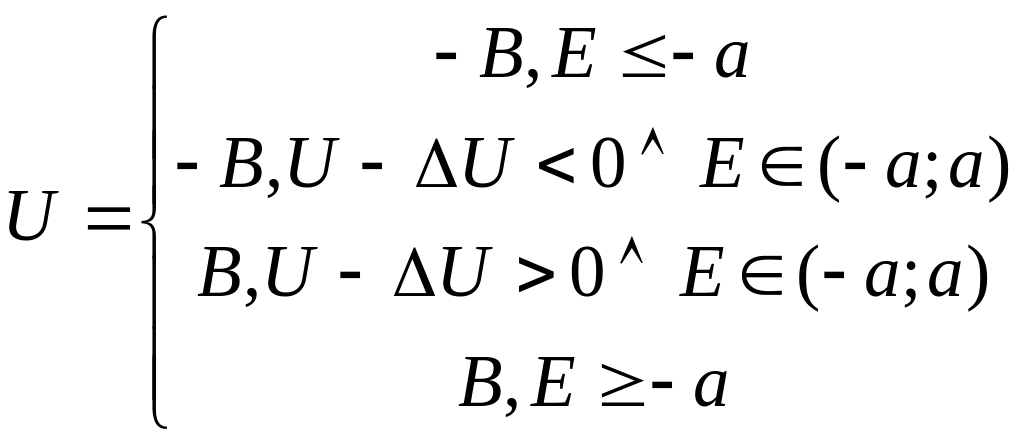^{при ΔU→0}

4. Реле общего вида.

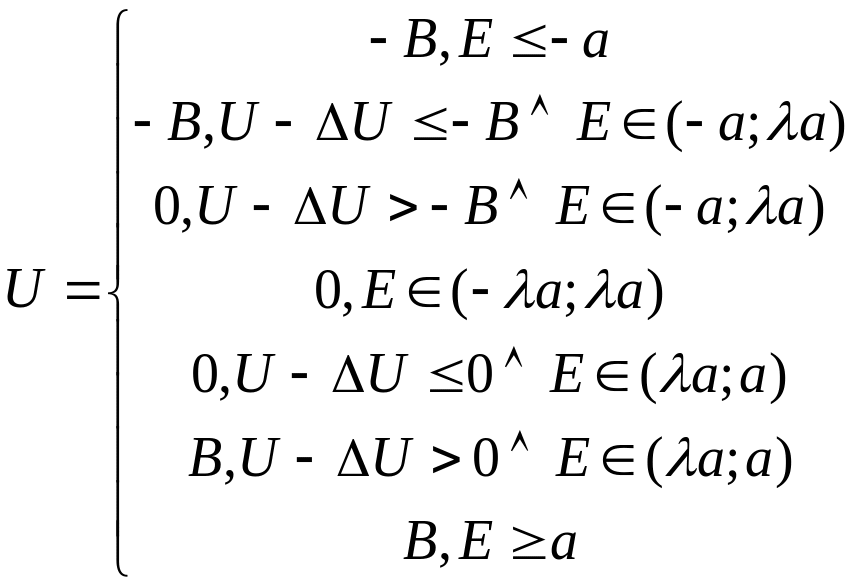
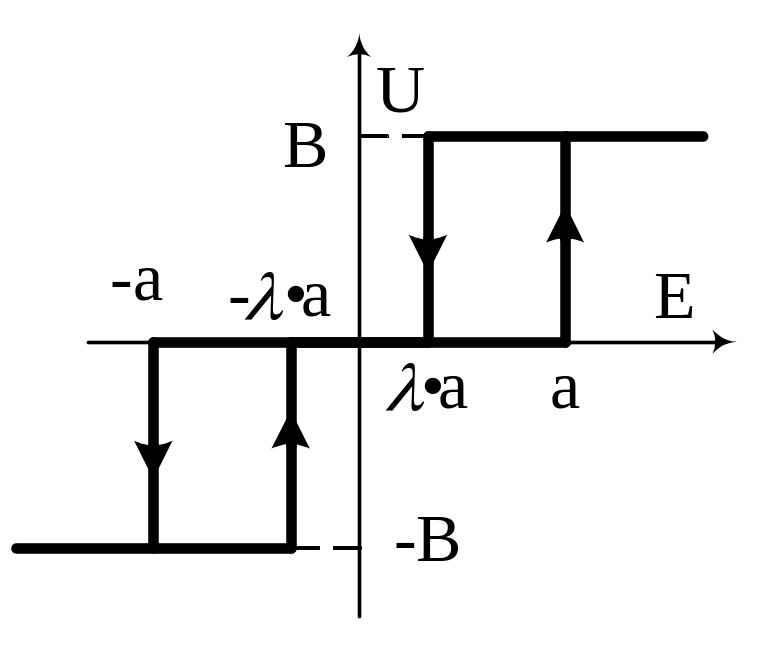при ΔU→0.

Здесь λ – коэффициент возврата. λ Є [-1;1]. Если λ=1 и a=0, то получается идеальное реле.

Подбирая параметры характеристики реле и охватывая её ОС , можно

реализовать любой из выше рассмотренных узлов. Все рассмотренные законы можно считать классическими. В настоящие время применяют и другие законы. Это нeчёткие регуляторы, управление с внутренней моделью.