
- •Нижегородский государственный университет им. Н.И. Лобачевского методические указания для решения задач на кратные интегралы
- •1. Двойные интегралы 5
- •2. Тройные интегралы 13
- •3. Поверхностные интегралы 21
- •Введение
- •1. Двойные интегралы
- •1.1. Свойства двойного интеграла
- •4. Монотонные свойства двойного интеграла.
- •1.2. Вычисление двойного интеграла
- •1.3. Изменение порядка интегрирования в двойном интеграле
- •1.4. Замена переменных в двойном интеграле
- •2. Тройные интегралы
- •2.1. Свойства тройного интеграла
- •4. Монотонные свойства тройного интеграла.
- •2.2. Вычисление тройного интеграла
- •2. Пусть теперь область интегрирования задается системой неравенств: { },
- •2.3. Замена переменных в тройном интеграле
- •3. Поверхностные интегралы
- •3.1. Способы задания поверхности
- •3.2. Сторона поверхности и её ориентация
- •3.3. Поверхностный интеграл первого рода
- •3.4. Сведение поверхностного интеграла первого рода к двойному.
- •3.5. Поверхностный интеграл второго рода
- •3.6. Сведение поверхностного интеграла второго рода к двойному
- •Литература
- •Методические указания для решения задач на кратные интегралы
- •603950, Нижний Новгород, пр. Гагарина, 23.
- •603600, Г. Нижний Новгород, ул. Большая Покровская, 37
1. Двойные интегралы
1.1. Свойства двойного интеграла
1.
Арифметические
свойства.
Если функции
![]() ,
,![]() интегрируемы
по области Q,
а числа ,
постоянные, то существует
интегрируемы
по области Q,
а числа ,
постоянные, то существует
![]()
![]() ,
,![]() )
)![]() .
.
По индукции это свойство распространяется на любое количество слагаемых.
2.Аддитивность
двойного интеграла
по областям. Если
область
![]() и
и
![]() ,
то
,
то
![]() .
.
Здесь
символом
![]() обозначена внутренность множества
обозначена внутренность множества
![]() .
Свойство аддитивности по области
нетрудно по индукции распространить
на любое конечное объединение области
с непересекающимися внутренностями.
.
Свойство аддитивности по области
нетрудно по индукции распространить
на любое конечное объединение области
с непересекающимися внутренностями.
3.
Интегрируемость
в подобласти. Если
существует
![]() ,
то существует
,
то существует
![]() по
любой ее квадрируемой подобласти
по
любой ее квадрируемой подобласти
![]() .
.
4. Монотонные свойства двойного интеграла.
а)
Если
![]() в области
в области![]() , то
, то
![]() ;
;
б)
Если
![]() в области
,
то
в области
,
то
![]()
![]() ;
;
в)
При существовании
существует![]() и
и
![]() ;
;
5.Двойной интеграл существует для любой непрерывной функции по квадрируемой области .
6.
Если ограниченная функция
непрерывна в квадрируемой
области
кроме
некоторого множества
![]() с площадью равной нулю, то
с площадью равной нулю, то
существует.
При этом, если изменить произвольным
образом значения
на множестве
![]() ,
то двойной интеграл от измененной
функции равен интегралу от прежней
функции.
,
то двойной интеграл от измененной
функции равен интегралу от прежней
функции.
1.2. Вычисление двойного интеграла
1.
Вычисление
в прямоугольнике.
Пусть функция
непрерывна в области
![]() .
Тогда двойной интеграл вычисляется по
формулам:
.
Тогда двойной интеграл вычисляется по
формулам:
![]() .
(1)
.
(1)
Таким образом мы сводим двойной интеграл к 2-м однократным (определенным ) интегралам по отрезку.
2. Вычисление по криволинейной трапеции. Если область Q криволинейная трапеция 1-го типа :
![]() ,
,
где
функции
![]() непрерывны на
непрерывны на
![]() и любая прямая x=
const
пересекает графики функций
и любая прямая x=
const
пересекает графики функций
![]() только в одной точке, то
только в одной точке, то
 .
(2)
.
(2)
Когда же область Q криволинейная трапеция 2-го типа:
![]() ,
,
где
функции
![]() - непрерывны на
- непрерывны на
![]() и любая прямая y=const
пересекает их график в одной точке,
то двойной интеграл вычисляем по формуле
и любая прямая y=const
пересекает их график в одной точке,
то двойной интеграл вычисляем по формуле
 .
(3)
.
(3)
По непрерывности подинтегральной функции будут существовать как двойной, так и определенные интегралы, соответствующие формулам (1),(2),(3). Таким образом и в случае криволинейной трапеции двойной интеграл вычисляется через два определенных интеграла. Это облегчает его вычисление и позволяет применять приемы интегрирования для определенного интеграла. Например, интегрирование по частям, замену переменных, таблицы интегралов и другие специальные способы.
1.3. Изменение порядка интегрирования в двойном интеграле
1. При вычислении двойных интегралов в криволинейной квадрируемой области часто приходится переходить от формул (2), (3) и наоборот. Этот способ называется изменением порядка интегрирования. Например, это диктуется удобством вычисления двойного интеграла по области . Важно также представлять область в виде объединения криволинейных трапеций 1-го и 2-го типов. В этом случае перейдем к сумме интегралов по этим подобластям и сводим двойной интеграл к сумме повторных. Изложим некоторые способы сведения двойных интегралов к повторным.
Пример
1. Изменить
порядок интегрирования в
 .
.
Решение.
Здесь
область
![]() и, как нетрудно видеть, является
криволинейной трапецией 1-го типа. Тогда
функции
и, как нетрудно видеть, является
криволинейной трапецией 1-го типа. Тогда
функции
![]()
![]() .
Для перехода к другому порядку
интегрирования представим область Q
в виде криволинейной трапеции 2-го типа
или как объединение этих трапеций.
Сначала найдем области изменения
переменных
.
Для перехода к другому порядку
интегрирования представим область Q
в виде криволинейной трапеции 2-го типа
или как объединение этих трапеций.
Сначала найдем области изменения
переменных
![]() и
и
![]() .
Используем для этого графическое
изображение области на рис.1:
.
Используем для этого графическое
изображение области на рис.1:


![]()

![]()




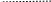

 Q
Q
x


1
1
2
Рис.1. Область Q примера 1.
Из
рис.1 видно, что при изменении
y
от 0 до 1 переменная
![]() будет
изменяться от
будет
изменяться от
![]() до
до
![]() .
Установим зависимость
.
Для этого выразим
из равенств для
:
.
Установим зависимость
.
Для этого выразим
из равенств для
:
![]() ,
которые
,
которые
будут
непрерывные. Как нетрудно видеть, здесь
любая прямая y=const
пересекает графики функций
![]() только в одной точке. Следовательно,
область Q
будет одновременно и криволинейной
трапецией 2-го типа. Тогда по (3) интеграл
только в одной точке. Следовательно,
область Q
будет одновременно и криволинейной
трапецией 2-го типа. Тогда по (3) интеграл
 .
.
Таким образом здесь осуществлена перестановка порядка интегрирования .
Пример
2 .
В
 сменить порядок интегрирования.
сменить порядок интегрирования.
Решение. Очевидно, область Q здесь будет трапецией 1-го типа:
![]() .
.
Но
Q
не является криволинейной трапецией
2-го типа. Действительно, здесь прямые
y=const
при
![]() пересекают график функции
пересекают график функции
![]() в двух точках. Это нетрудно увидеть из
рис.2
в двух точках. Это нетрудно увидеть из
рис.2
1

 y
y





x

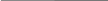

2
Рис.2. Область примера 2.
Поэтому
для изменения порядка интегрирования
представим область Q
как
объединение криволинейных трапеций
2-го типа. С этой целью выразим переменную
x
из равенств для функций
![]() .
Тогда получаем
.
Тогда получаем
![]()
![]() .
Если провести прямую y=1,
то получим разбиение Q
на
.
Если провести прямую y=1,
то получим разбиение Q
на
![]() ,
,
![]() ,
,
![]() .
.
Очевидно,
![]() и пересечение их внутренностей пусто.
Из аддитивного свойства двойного
интеграла по областям получаем:
и пересечение их внутренностей пусто.
Из аддитивного свойства двойного
интеграла по областям получаем:
![]() .
.
Но
![]() являются криволинейными трапециями
2-го типа. Поэтому,
являются криволинейными трапециями
2-го типа. Поэтому,
расставляя пределы интегрирования, получаем:
 .
.
Отсюда
получаем требуемое, так как
 .
.
Пример
3. Вычислить
![]() .
.
Решение. Здесь область интегрирования Q ,как нетрудно видеть, повернутый квадрат. Разобьем область интегрирования на две криволинейные трапеции 1-го типа:
![]() ,
,
![]() .
.
Здесь
пересечение внутренних областей
![]() пусто. Тогда по свойству двойного
интеграла получаем
пусто. Тогда по свойству двойного
интеграла получаем
 .
.
Окончательное вычисление предоставляем читателю. Отметим, что здесь область Q можно представить и как объединение трапеций 2- го типа.
2. К разбиению области Q на трапеции 1-го или 2-го типов приводят и задачи на интегрирование разрывных функций. В этом случае выделяют подобласти, где функция непрерывна и имеет аналитическое выражение .
Пример
4.
Вычислить
![]() где
где
![]() .
.
Решение.
Здесь![]() имеет конечный разрыв на кривой
имеет конечный разрыв на кривой
![]() – множестве с площадью нуль. Поэтому
двойной интеграл существует.
– множестве с площадью нуль. Поэтому
двойной интеграл существует.
![]() ,
,
![]() .
.
Т
![]() ,
,
где
Q1
и
Q2
- трапеции 1-го типа. Но функция
![]() в подобласти
в подобласти
![]() .
Отсюда
.
Отсюда
![]() =0.
=0.
