
- •ПРЕДИСЛОВИЕ
- •1. Действительные числа
- •1.1. Каноническое разложение натурального числа:
- •1.2. Некоторые признаки делимости натуральных чисел.
- •1.3. Абсолютная величина (модуль) действительного числа:
- •1.4. Дроби.
- •1.5. Пропорции.
- •1.6. Степени и логарифмы.
- •2. Алгебра.
- •2.1. Формулы сокращенного умножения.
- •2.2. Формулы Виета.
- •2.4. Корни кубичного уравнения с действительными коэффициентами.
- •2.5. Корни уравнения 4-й степени.
- •2.6. Неравенства.
- •2.7. Комбинаторика и бином Ньютона.
- •1. Элементарная геометрия
- •1.1. Треугольники.
- •1.2. Четырехугольники.
- •1.3. Многоугольник.
- •1.4. Окружность и круг.
- •1.5. Сегмент и сектор.
- •1.7. Пирамида.
- •1.8. Правильные многогранники.
- •1.11. Сфера и шар.
- •1.12. Части шара.
- •2. Аналитическая геометрия
- •2.1. Прямая на плоскости.
- •2.2. Плоские линии второго порядка. Эллипс. Гипербола. Парабола.
- •2.3. Плоскость.
- •2.4. Прямые в пространстве.
- •2.5. Поверхности второго порядка.
- •3. Дифференциальная геометрия
- •3.1. Линии на плоскости.
- •3.2. Линии в пространстве.
- •3.3. Подвижный трехгранник Френе пространственной кривой.
- •3.4. Поверхности в трехмерном пространстве.
- •4. Векторы и векторные функции
- •4.1. Векторная алгебра.
- •4.2. Некоторые формулы векторного анализа.
- •1. Числовые последовательности
- •1.1. Основные определения.
- •1.2. Основные свойства пределов последовательностей.
- •1.3. Пределы некоторых последовательностей.
- •2. Производные и дифференциалы
- •2.1. Основные определения.
- •2.3. Свойства производных и дифференциалов высшего порядка.
- •2.4. Производные от элементарных функций.
- •2.5. Частные производные и дифференциалы.
- •3. Первообразная и неопределенный интеграл
- •3.1. Основные определения.
- •3.2. Свойства неопределенного интеграла.
- •3.3. Некоторые неопределенные интегралы от элементарных функций.
- •4. Некоторые неопределенные интегралы
- •4.1. Интегралы от рациональных функций.
- •4.2. Интегралы от иррациональных функций.
- •4.3. Интегралы от тригонометрических функций.
- •4.4. Интегралы, содержащие показательную функцию.
- •4.5. Интегралы, содержащие логарифмическую функцию.
- •4.6. Интегралы, содержащие обратные тригонометрические функции.
- •4.7. Интегралы, содержащие гиперболические функции.
- •5. Определенный интеграл
- •5.1. Основные определения.
- •5.2. Свойства определенного интеграла.
- •5.3. Приложения определенного интеграла.
- •5.4. Некоторые определенные интегралы.
- •6.1. Основные определения.
- •6.2. Несобственные интегралы.
- •6.3. Интегралы, зависящие от параметра.
- •6.4. Несобственные интегралы, зависящие от параметра.
- •7. Кратные интегралы
- •8. Криволинейные интегралы
- •9. Поверхностные интегралы
- •IV. Ряды и произведения
- •1. Числовые ряды
- •1.1. Основные определения.
- •1.2. Действия с рядами.
- •1.4. Признаки сходимости знакопеременных рядов.
- •1.5. Свойства рядов.
- •1.6. Некоторые конечные суммы.
- •1.7. Некоторые числовые ряды.
- •2. Функциональные ряды
- •2.1. Основные определения.
- •2.2. Признаки сходимости функциональных рядов.
- •2.3. Свойства функциональных рядов.
- •2.4. Формулы для вычисления радиуса сходимости R степенного ряда
- •2.5. Действия со степенными рядами.
- •2.6. Некоторые степенные ряды.
- •3. Бесконечные произведения
- •3.1. Основные определения
- •3.2. Свойства бесконечных произведений.
- •3.3. Некоторые бесконечные произведения.
- •V. КОМПЛЕКСНЫЕ ЧИСЛА И ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- •1. Комплексные числа
- •2. Функции комплексного переменного
- •2.1. Основные определения.
- •2.2. Дифференцирование функций комплексного переменного.
- •2.3. Интегрирование функций комплексного переменного.
- •2.4. Ряды.
- •2.5. Вычеты.
- •2.6. Конформные отображения.
- •VI. Трансцендентные функции
- •1. Тригонометрические функции
- •1.1. Некоторые значения тригонометрических функций.
- •1.2. Связь между тригонометрическими функциями одного аргумента.
- •1.3. Формулы приведения.
- •2. Гиперболические функции
- •3. Гамма-функция
- •4. Функции Бесселя
- •5. Модифицированные функции Бесселя I и K
- •6. Вырожденные гипергеометрические функции
- •7. Некоторые интегральные функции
- •СПИСОК ЛИТЕРАТУРЫ
96 |
|
|
|
|
|
|
|
|
|
|
VI. Трансцендентные функции |
|
|||
|
|
|
1. Тригонометрические функции |
|
|||
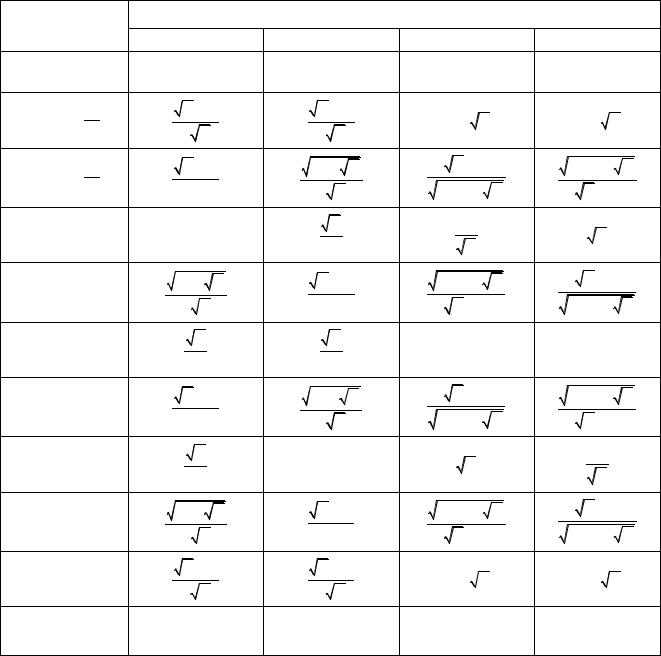
1.1. Некоторые значения тригонометрических функций. |
|
||||||
Аргумент |
|
|
Функция |
|
|||
sin α |
cos α |
tg α |
ctg α |
||||
|
|
|
|||||
0° |
(0) |
0 |
1 |
0 |
не определен |
||
15° |
|
π |
3 −1 |
3 +1 |
2 − 3 |
2 + 3 |
|
|
|
2 2 |
2 2 |
||||
|
|
12 |
|
|
|||
18° |
|
π |
5 −1 |
5 + 5 |
5 −1 |
10 + 2 5 |
|
|
|
4 |
2 2 |
10 + 2 5 |
5 −1 |
||
|
|
10 |
|||||
30° |
|
π |
1 |
3 |
1 |
3 |
|
|
|
2 |
2 |
3 |
|||
|
|
6 |
|
||||
36° |
|
π |
5 − 5 |
5 +1 |
10 − 2 5 |
5 +1 |
|
|
|
2 2 |
4 |
5 +1 |
10 − 2 5 |
||
|
|
5 |
|||||
45° |
|
π |
2 |
2 |
1 |
1 |
|
|
|
2 |
2 |
||||
|
|
4 |
|
|
|||
54° |
|
3π |
5 +1 |
5 − 5 |
5 +1 |
10 − 2 5 |
|
|
|
4 |
2 2 |
10 − 2 5 |
5 +1 |
||
|
|
10 |
|||||
60° |
|
π |
3 |
1 |
3 |
1 |
|
|
|
2 |
2 |
3 |
|||
|
|
3 |
|
||||
72° |
|
2π |
5 + 5 |
5 −1 |
10 + 2 5 |
5 −1 |
|
|
|
2 2 |
4 |
5 −1 |
10 + 2 5 |
||
|
|
5 |
|||||
75° |
|
5π |
3 +1 |
3 −1 |
2 + 3 |
2 − 3 |
|
|
|
2 2 |
2 2 |
||||
|
|
12 |
|
|
|||
90° |
|
π |
1 |
0 |
не определен |
0 |
|
|
|
||||||
|
|
2 |
|
|
|
|
|
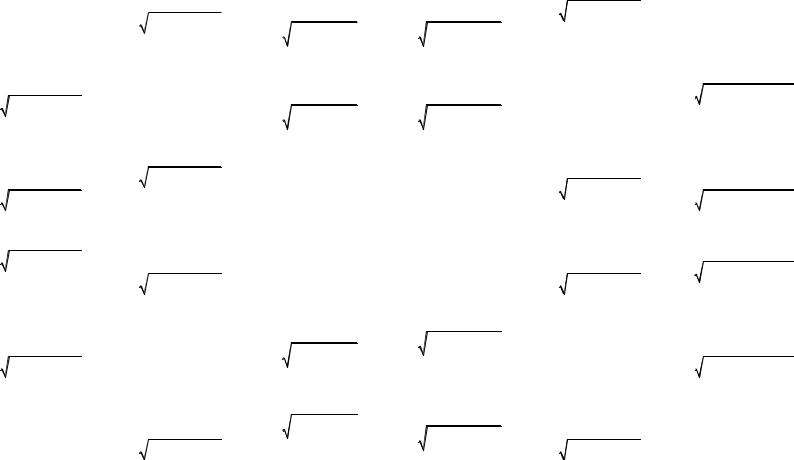
1.2. Связь между тригонометрическими функциями одного аргумента.
(в приведенных формулах перед знаком радикала должен быть выбран «плюс» или «минус», в зависимости от того, в какой четверти находится угол α, а именно, таким образом, чтобы знак тригонометрической функции, стоящей в левой части, совпадал со знаком величины, стоящей в правой части равенства)
|
|
sin α |
|
|
|
cos α |
|
|
|
|
tg α |
|
|
|
|
|
ctg α |
|
|
|
|
|
sec α |
|
|
|
cosec α |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin α |
|
|
= |
|
|
|
|
|
2 |
|
|
= |
|
|
tg α |
|
|
|
= |
|
|
|
1 |
|
|
|
|
= |
± |
sec |
2 |
α −1 |
|
|
|
= |
1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
= ± 1 |
− cos |
α |
|
± 1 + tg2 α |
|
± 1 |
+ ctg2 α |
|
|
sec α |
|
|
|
cosec |
α |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
cos α |
|
|
2 |
|
|
|
|
= |
|
|
|
= |
|
|
1 |
|
|
|
|
= |
|
|
ctg α |
|
|
|
|
|
= |
1 |
|
|
|
= |
± cosec2 α −1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
= ± 1 |
− sin |
α |
|
|
|
|
|
± 1 + tg2 α |
|
± 1 |
+ ctg2 α |
|
|
|
sec α |
|
|
cosec α |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
tg α |
= |
sin α |
|
|
= |
± 1 |
− cos2 α |
|
|
|
= |
|
|
|
|
|
|
= |
|
1 |
|
|
|
|
= ± sec2 α −1 |
= |
|
|
1 |
|
|
|
|
||||||||||||||
± 1 |
− sin2 α |
|
|
|
|
|
|
|
|
|
ctg α |
|
|
|
± cosec2 α −1 |
||||||||||||||||||||||||||||||||
|
|
|
cos α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ctg α |
= |
± 1 |
− sin2 α |
= |
cos α |
|
|
|
|
= |
1 |
|
|
|
|
|
|
|
|
= |
|
|
|
|
= |
|
|
1 |
|
|
|
= ± |
cosec |
2 |
α −1 |
||||||||||||
± 1 |
− cos2 α |
|
|
tg α |
|
|
|
|
|
|
|
|
|
|
|
± sec2 α −1 |
|||||||||||||||||||||||||||||||
|
sin α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
= |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
± 1 |
+ ctg2 α |
|
|
|
|
|
|
|
|
|
= |
|
|
cosec α |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
sec α |
± 1 |
− sin2 α |
|
= cos α |
|
|
= ± |
1 + tg |
α |
= |
|
|
ctg α |
|
|
|
|
|
|
= |
|
|
|
|
± cosec2 α −1 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
= |
|
1 |
|
|
|
|
± 1 + tg2 α |
|
|
|
|
|
|
2 |
|
|
= |
|
|
sec α |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
cosec α |
|
= sin α |
|
|
± 1 |
− cos2 α |
= |
|
|
tg α |
|
|
|
= ± |
1 |
+ ctg |
α |
± sec2 α −1 |
|
|
|
= |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
ФУНКЦИИ ТРИГОНОМЕТРИЧЕСКИЕ .1.VI
97
98 |
VI.1. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ |
|
|||||||
1.3. Формулы приведения. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аргумент |
|
|
Функция |
|
|
|
|
|
|
|
|
|
β = π ± α |
|
β = π ± α |
|
β = 3π ± α |
β = 2π − α |
||||
|
|
|
|||||||
|
2 |
|
|
|
|
|
|
2 |
|
sin β = |
cos α |
|
sin α |
|
|
– cos α |
– sin α |
||
cos β = |
sin α |
|
– cos α |
|
|
± sin α |
cos α |
||
tg β = |
ctg α |
|
± tg α |
|
|
ctg α |
– tg α |
||
ctg β = |
tg α |
|
± ctg α |
|
|
tg α |
– ctg α |
||
|
|
|
|
|
|
|
|||
Тригонометрические функции суммы и разности двух углов: |
|
||||||||
sin (α ± β) = sin α cos β ± cos α sin β; |
|
cos (α ± β) = cos α cos β sin α sin β; |
|||||||
|
|
|
tg α ± tg β |
|
|
ctg α ctg β 1 |
|||
|
tg (α ± β) = |
|
; |
ctg (α ± β) = ctg β ± ctg α . |
|||||
|
1 tg α tg β |
||||||||
Тригонометрические функции двойных, тройных и половинных аргументов:
sin 2α = 2 sin α cos α; cos 2α = cos2 α – sin2 α = 1 – 2 sin2 α = 2 cos2 α – 1;
tg 2α = |
|
2 tg α |
; |
|
|
|
ctg 2α = |
|
|
ctg2 α −1 |
; |
|
|
|||||||
|
− tg2 α |
|
|
|
|
|
2 ctg α |
|
|
|||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
sin 3α = 3 sin α – 4 sin3 α; |
|
|
|
cos 3α = 4 cos3 α – 3 cos α; |
||||||||||||||||
tg 3α = |
3 tg α − tg3 α |
; |
|
|
|
ctg 3α = |
ctg3 α − 3 ctg |
α |
; |
|||||||||||
|
1 |
− 3 tg2 α |
|
|
|
|
|
3 ctg2 α −1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
sin |
α |
= ± |
1 − cos α; |
|
|
|
cos α |
= ± 1 + cos α |
; |
|
|
|||||||||
|
2 |
|
|
|
|
2 |
|
|
2 |
|
|
|
2 |
|
|
|
|
|||
tg α |
= ± |
1 − cos α |
= |
|
|
sin α |
|
= |
|
|
1 − cos α |
; |
|
|
|
|||||
1 + cos α |
1 + cos α |
|
|
|
|
|
||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
sin α |
|
|
|
|||||||
ctg |
α |
= ± |
1 + cos α |
= |
|
|
sin α |
= |
|
1 + cos α . |
|
|
|
|||||||
2 |
1 − cos α |
|
1 − cos α |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
sin α |
|
|
|
|||||||
В формулах половинного угла знаки перед радикалами берутся в зависимости от знака тригонометрической функции, стоящей в левой части равенства.
Преобразование суммы (разности) тригонометрических функций в произведение:
sin α + sinβ = 2sin |
α + β cos α − β ; |
|
sin α − sin |
β = 2cos |
α + β sin |
α − β |
; |
|||||
|
2 |
2 |
|
|
|
|
|
2 |
|
2 |
|
|
|
cos α + cosβ = 2 cos |
α + β cos α − β ; |
|
|
|
|
||||||
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
cos α − cosβ = −2sin |
α + β sin |
α − β = 2sin |
α + β sin |
β − α |
; |
|
|
|||||
|
|
|
2 |
|
2 |
2 |
|
2 |
|
|
|
|
cos α + sin α = |
2 cos (45° − α); |
|
cos α − sin α = 2 sin (45° − α); |
|
||||||||
tg α ± tg β = |
sin (α ± β) |
; |
|
ctg α ± ctg β = |
sin (β ± α) |
; |
|
|
||||
|
|
sin αsinβ |
|
|
||||||||
|
|
cos αcosβ |
|
|
|
|
|
|
||||

1.3. ФОРМУЛЫ ПРИВЕДЕНИЯ. |
99 |
tg α + ctg β = |
cos (α − β) |
|
; |
|
tg α − ctg β = |
cos (α + β) |
; |
|
|
||||||||||||||||
cos αsinβ |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
cos αsinβ |
|
|
||||||||||||||
|
tg α + ctg α = 2 cosec 2α; |
tg α − ctg α = −2 ctg 2α; |
|
|
|||||||||||||||||||||
|
1 + cos α = |
2 |
α |
; |
|
|
|
|
|
|
|
|
|
|
2 |
α |
; |
|
|
|
|
|
|||
|
2 cos |
2 |
|
|
|
|
1 − cos α = 2sin |
2 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
α |
|
; |
2 |
|
|
|
α |
|
; |
|||||||||||||
1 + sin α = 2 cos |
45° − |
2 |
|
|
1 − sin α = 2sin |
45° − |
2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 sin (45° ± α) |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 ± tg α = |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
cos α |
|
|
|
|
|
|
|
|
|||||
1 |
± tg αtg β = |
cos (α β) |
; |
|
|
|
|
ctg αctg β ±1 = |
cos(α β) |
|
; |
|
|||||||||||||
cos αcosβ |
|
|
|
|
sin αsinβ |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
1 − tg2 α = cos 2α |
|
; |
|
|
|
|
1 − ctg2 α = − cos 2α |
; |
|
|
|
|
|
|
||||||||||
|
|
|
|
cos2 α |
|
|
|
|
|
|
|
sin2 α |
|
|
|
|
|
|
|
||||||
|
tg2 α − tg2 β = |
sin (α + β)sin (α − β) |
; |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
cos2 αcos2 β |
|
|
|
|
|
|
|
|
|||||
|
ctg2 α − ctg2 β = |
sin (α + β)sin (β − α) |
; |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
sin2 αsin2 β |
|
|
|
|
|
|
|
|
|||||
tg2 α − sin2 α = tg2 α sin2 α; |
|
|
|
ctg2 α − cos2 α = ctg2 α cos2 α. |
|||||||||||||||||||||
Преобразование произведения тригонометрических функций в сумму: sin αsin β = 12 cos (α − β) − cos (α + β) ;
cos αcos β = 12 cos (α − β) + cos (α + β) ; sin αcos β = 12 sin (α − β) + sin (α + β) ;
sin αsinβsin γ = |
1 |
sin (α + β − γ) + sin (β + γ − α) + sin (γ + α − β) − sin (α + β + γ) ; |
|
||||||||||||||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin αsinβcos γ = |
1 −cos |
( |
α + β − γ |
) |
+ cos |
( |
β + γ − α |
) |
+ cos |
( |
γ + α − β |
) |
− cos |
( |
α + β + γ |
|
; |
||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin αcosβcos γ = |
1 sin |
( |
α + β − γ |
) |
− sin |
( |
β + γ − α |
) |
+ sin |
( |
γ + α − β |
) |
+ sin |
( |
α + β + γ |
; |
|
||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos αcosβcos γ = |
1 |
cos (α + β − γ) |
+ cos (β + γ − α) |
+ cos(γ + α − β) |
+ cos(α + β + γ) . |
||||||||||||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Соотношения между обратными тригонометрическими функциями: arcsin x = −arcsin (−x) = 2π − arccos x = arctg (x 1 − x2 );
1 − x2 );
arccos x = π − arccos (−x) = 2π − arcsin x = arcctg (x 1 − x2 ); arctg x = −arctg (−x) = 2π − arcctg x = arcsin (x
1 − x2 ); arctg x = −arctg (−x) = 2π − arcctg x = arcsin (x 1 + x2 ); arcctg x = π − arcctg (−x) = 2π − arctg x = arccos (x
1 + x2 ); arcctg x = π − arcctg (−x) = 2π − arctg x = arccos (x 1 + x2 ).
1 + x2 ).
