§ 15. Конические зубчатые передачи. Устройство и основные геометрические и силовые соотношения

3.66. Зубчатую передачу с пересекающимися осями, у которой начальные и делительные поверхности колес конические, называют конической.

Коническая передача состоит из двух конических зубчатых колес (рис. 3.45) и служит для передачи вращающего момента между валами с пересекающимися осями под углом δ₁ + δ₂ = ∑. Наиболее распространена в машиностроении коническая передача с углом между осями Z = 90⁰ (рис. 3.47), но могут быть передачи ис ∑ ≥ 90°. Колеса конических передач. выполняют с прямыми (рис. 3.46, а), косыми (рис. 3.46, б), круговыми.

Рис. 3.45. Коническая пря­мозубая передача

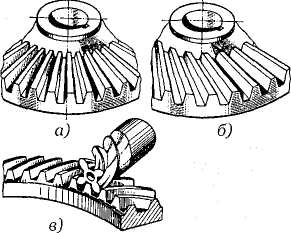
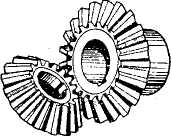
Рис. 3.46. Конические зубчатые колеса: а — коле­со с прямыми зубьями; б — колесо с косыми зу­бьями; в — колесо с круговыми зубьями

Рис. 3.47. Геометрические параметры конических зубчатых колес

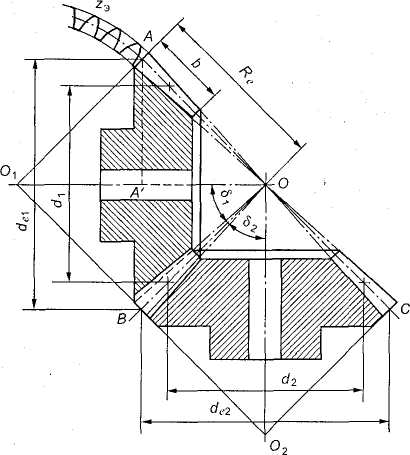
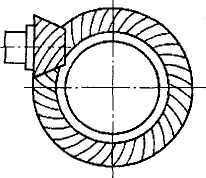
Рис. 3.48. Гипоиднаяя передача

зубьями (рис. 3.46, в).

Передачу с коническими колесами для передачи вращающего момента между валами со скрещиваю­щимися осями называют гипоидной (рис. 3.48). Эта передача находит применение в автомобилях.

По стоимости конические передачи дороже ци­линдрических при равных силовых параметрах. Их применение диктуется только необходимостью пе­редавать момент при пересекающихся осях валов. Передаточное число одной пары и ≤ 6,3.

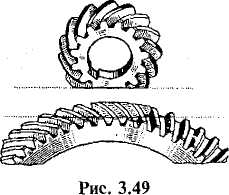
С какими зубьями выполнены шестерня и колесо, показанные на рис. 3.49?

3.67. Вершины начальных и делительных конусов конической передачи на­ходятся в точке пересечения осей валов О (рис. 3.50). Высота и толщина зубьев уменьшаются по направлению к вершинам конусов. Геометрические параметры конической передачи (рис. 3.47 и 3.50):

А О В — делительный конус шестерни;

ВОС — делительный конус колеса;

АО₁ В — делительный дополнительный конус шестерни;

ВО₂С — делительный дополнительный конус колеса;

δ₁ — угол делительного конуса шестерни;

δ₂ — угол делительного конуса колеса;

d_e[ — внешний делительный диаметр шестерни;

d_e2 — то же, колеса;

d₁ — средний делительный диаметр шестерни;

d₂ — то же, колеса;

b — ширина зубчатого венца (длина зуба);

R_e — внешнее делительное конусное расстояние (или длина дис­танции).

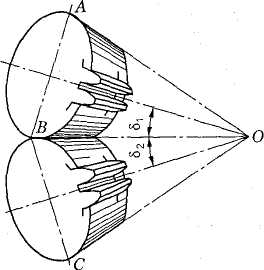
Рис. 3.50. Коническая прямозубая передача

3.68. Передаточное число конической передачи определяется так:

3.69. В конической передаче может быть бесчисленное множество делительных окружностей. Для расчета в машиностроении принимают внешнюю и среднюю делительные окружности (см. рис. 3.47).

Из условия, что в конической передаче модуль и делительный связаны теми же соотношениями, что и в цилиндрических передачах, т. с. d=mz (рис. 3.51), определяют внешний d_e и средний d_m делительные метры:

где т_е — внешний окружной модуль; т_т — средний окружной модуль.

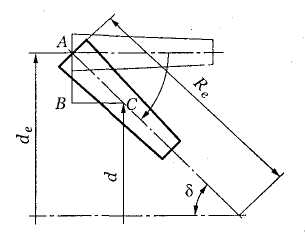
Рис. 3.51. Зуб конического колеса

Внешний окружной модуль обычно выбирают из стандартного ряда (см. табл. 3.1). Округление внешнего модуля до стандартного значения не является обязательным требованием. Этот модуль называют производственным и по его значению определяют все геометрические параметры зубча­тых колес (задают размеры зубьев на внешнем торце, на котором удобно производить измерения).

Средний окружной модуль т рассчитывают в зависимости от внешнее окружного модуля т_е. По среднему окружному модулю производят расчет передачи на прочность при изгибе.

Покажите на рис. 3.53 высоту зуба h_ae и h_am.

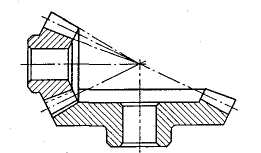
Рис. 3.52

3.70. Зависимость между т_е и т_т в конической передаче.

Из рис. 3.51 r_е = r + АВ, где AB = (из ∆ABC. Отсюда .

Умножив левую и правую части равенства на два, получим d_e= d + bsinδ. Разделив левую и правую части равенства на z, получим

.

3.71. Геометрические соотношения размеров прямозубой конической пере­дачи с эвольвентным профилем зуба. Согласно рис. 3.53 внешний диаметр вершин зубьев

d_ae = d_e + 2АВ = m_ez + 2m_ecos δ = m_e(z + 2 cos δ);

внешний диаметр впадин зубьев

dfe = d_e - 2AС = m_ez - 2,4m_ecosδ = m_e(z - 2,4 cosδ).

Длина зуба (ширина венца) b = Ψ_bdd₁ [Ψ_bd= 0,3 ÷ 0,6 при условии Ψ_bRe = b/R_e ≤ 0,3 и b < 10т_е, где d_t — средний делительный диаметр шес­терни].

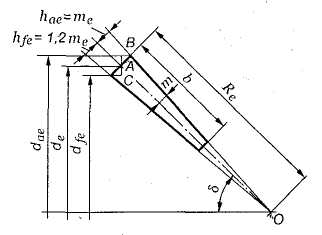
Рис. 3.53. Геометрия прямозубой конической передачи

Ориентировочно длина зуба может быть выбрана также в зависимости от внешнего делительного конусного расстояния R_e:

R_e /4≤b≤R_e /3.

Таблица 3.15. Геометрические параметры прямозубой конической передачи

	Параметр, обозначение		Расчетные формулы
	Внешний окружной модуль те
	Средний окружной модуль т
	Внешний диаметр вершин зубьев dac		dm, = mc{z + 2 cos δ)
	Внешний делительный диаметр de		dc, = me z
	Внешний диаметр впадин зубьев dfe		dfi = me(z - 2,4 cos δ)
	Высота зуба he		he = 2,2m,
	Высота головки зуба hae		hlK = me
	Высота ножки зуба hfe		hft =\,2me
	Окружной шаг pie		Pic =πme
Окружная толщина зуба ste
Окружная ширина впадины е1е
Радиальный зазор се		се = 0,25 тс
Ширина зубчатого венца Ъ
Внешнее делительное конусное расстояние Re
Угол делительного конуса шестерни δ1		δ1 =90°- δ2
колеса δ2		tgδ2 = и

3.72. Силы в зацеплении прямозубой конической передачи. В рассматривае­мой передаче действует одна сила, обусловленная давлением зуба шестерни на зуб колеса. Эта сила для удобства расчетов раскладывается на 3 состав­ляющие: окружная F_t, радиальная F_r и осевая F_a.

С учетом геометрических соотношений в конической передаче по нор­мали к зубу действует сила F_nX (рис. 3.54). Эту силу разложим на две состав­ляющие: F_n и F'_rl. В свою очередь F'_ri разложим на F_al и F_rl. Запишем:

a; F'_Fl = F,fea; F_r] = F'_r] cos 5, = F_ntga cos 5,; " F_ai = F'_rl sin 8, = /'„tgasinS,;

Осевая сила на шестерне численно равна радиальной силе на колесе.

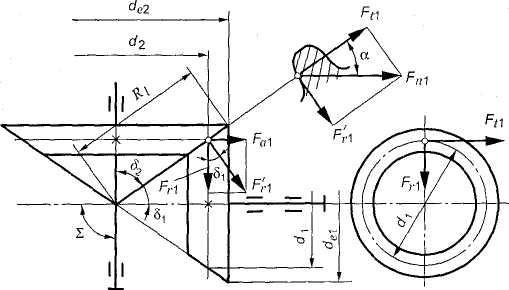
Рис. 3.54. Силы в зацеплении прямозубой конической передачи

3.73. Ответить на вопросы контрольной карточки 3.10.

Контрольная карточка 3.10

Вопрос	Ответы	Код
По отпечатку зуба (рис. 3.55) в М 1:1 определите модуль зацепления (мм)	13,5 11,0 7,5 6,0 3,0	1 2 3 4 5
Какой модуль может быть принят стандартным в конической передаче?	те тт Оба	6 7 8
Пользуясь каким модулем рассчитывают диаметр окружности впадин в конической передаче?	те тт те и т,„	9 10 11
Чему равна высота (мм) головки зуба, если колесо имеет 45 зубьев (см. рис. 3.56); de\ = 51 мм, de2 = 225 мм?	3,75 11,25 5,0 6,25 По этим данным нельзя подсчитать	12 13 14 15 16
Покажите на рис. 3.56 диаметр окружности впадин шестерни	dae1 de1 dfe1 D1	17 18 19 20

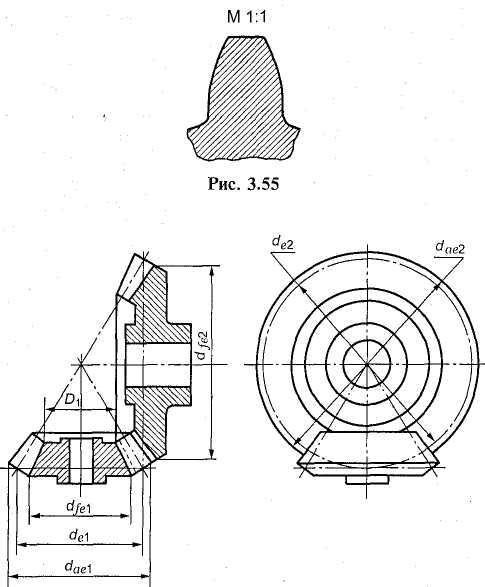
Рис. 3.56